Принцип физичности

Максимальная точность определения (измерения) свойств системы зависит от присущей данной системе области неопределенности, внутри которой повышение точности определения (измерения) одного свойства влечет за собой снижение точности определения другого (других).

Принцип неопределенности хорошо известен из квантовой механики: произведение ошибки в измерении координаты на ошибку в измерении импульса частицы не может быть меньше постоянной Планка при какой бы то ни было точности эксперимента.

Математическое определение постулата неопределенности. При t>0 любое измерение связано с затратой времени, в течение которого измеряемый динамический процесс и связанные с ним процессы изменятся. Чем точнее измерение 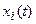,тем сильнее изменится 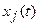и тем больше ошибка в его измерении. Поэтому для любой пары процессов 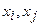имеем 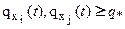, где 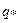- порог. Тогда

.

Всякой системе (независимо от ее природы) присущи физические законы (закономерности), возможно уникальные, определяющие внутренние причинно-следственные связи, существование и функционирование. Никаких других законов (кроме физических) для объяснения действия систем любой природы (в том числе живых) не требуется.

Принцип физичности включает несколько постулатов.

Постулат целостности: Система (как целое) обладает особым, системным свойством (свойствами), которого нет у подсистем (элементов) при любом способе декомпозиции.

Системные свойства формируются путем накопления, усиления и проявления одних свойств подсистем одновременно с нивелированием, ослаблением и скрытием других при взаимодействии подсистем. Происходит скачок - переход количества в качество.

Сущность постулата целостности состоит в том, что ни при декомпозиции, т.е. объединении подсистем в систему, ни при декомпозиции, т.е. членении системы, недопустима потеря понятий.

Сущность постулата целостности состоит в том, что композиция и декомпозиция должны осуществляться в направлении генерирования характеризующей систему информации более высокого качества.

Применение постулата целостности состоит в раскрытии и накоплении сведений о системных свойствах на всех этапах исследования и в обобщении их в понятия, а затем - в применении этих понятий к подсистемам при исследовании их порознь после декомпозиции

Рациональность декомпозиции оценивается на основании определения целостности: если декомпозиция неудачна, системные и подсистемные понятия невозможно увязать, между ними теряется преемственность, они неустойчивы и производят случайное впечатление.

Математическое определение постулата целостности. Пусть система S имеет конечное множество 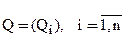системных свойств.

Для определенности примем, что все свойства Q_i имеют числовую меру, не обязательно единую (в принципе такое допущение не обязательно, но упрощает запись).

Пусть возможно m вариантов (способов) декомпозиции (m конечно или бесконечно). При r-й 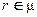декомпозиции 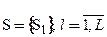(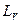- число подсистем в S). Каждая подсистема характеризуется конечным множеством свойств 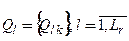, каждое свойство имеет числовую меру, вообще говоря, индивидуальную. Множество свойств всех 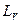подсистем системы при r-й декомпозиции 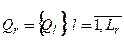.Взаимодействуя, подсистемы порождают конечное множество системных процессов:

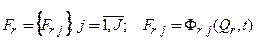
Системное свойство 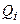есть функционал 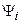от протекающих в системе процессов:

.

Постулат целостности состоит в том, что

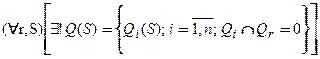
Это означает, что: "для всех 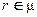системы S существует единственное множество 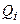, зависящее только от S и не зависящее от r, такое, что 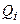в и в 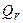не существует ни одного общего элемента".

Постулат декомпозиции. систем Анализ и синтез сложной системы управления осуществляется путем расчленения ее на подсистемы, располагаемые по уровням, причем подсистема на данном уровне является системой на нижележащем уровне и\. в свою очередь. рассматривается как элемент вышележащего уровня.

Постулат автономности: интересующая нас система расположена в адекватном ей геометрическом пространстве (реальном, функциональном, мысленном) и ограничиваясь метрическими пространствами, мы должны каждому классу систем (конкретной системе) приписать метрику, определяемую соответствующей группой преобразований. Это - автономная метрика системы, либо автономная группа преобразований.

Сложная система находится в реальном геометмире и взаимодействует с ним, но основное значение для ее свойств имеют процессы, которые протекают внутри системы. Познание системы требует прежде всего ее обозримого описания, и здесь выбор метрики может играть определяющую роль. Расстояние в евклидовом пространстве между клетками живого организма очень мало связано с такими функциональными свойствами, как время передачи возбуждения, время реакции и т.д. Значительно эффективнее использовать функциональное пространство с соответствующим числом измерений и автономной метрикой. В сущности сложная система и "живет" в автономном функциональном пространстве. Все, что происходит в системе, описывается в этом пространстве более просто. Введение метрики означает создание модели геометрии системы.

Итак, сложные системы имеют автономную пространственно-временную метрику, для них существует автономное расстояние и автономное время. Релятивистское время высокоэнергетических частиц - только один пример автономной метрики. Сложные системы могут иметь локальный масштаб времени, отличный от астрономического. Для развивающихся систем он может быть различным на различных этапах развития.

С точки зрения постулата целостности разнообразие декомпозиций помогает выявлению системных свойств. С точки зрения постулата автономности большинство декомпозиций, а может быть все кроме одной, отпадут. Останется единственная декомпозиция, которая соответствует автономной метрике системы. Поскольку каждый класс физических явлений отождествляется с определенным набором инвариантов, каждая группа преобразований и порожденная ею геометрия соответствует этому же набору.

Некоторые инварианты или функции от них не изменяются при взаимодействии подсистем, сохраняя значение постоянным и допуская только его перераспределение между подсистемами. Тогда говорят, что соответствующая физическая величина подчиняется закону сохранения. Скорость - инвариант, но закона сохранения скорости нет. Однако произведение массы на квадрат скорости не изменяется ни при каких взаимодействиях: это закон сохранения энергии.

Но существуют более узкие, внутрисистемные "законы сохранения", определяемые устройством системы. В солнечной системе (при точечном представлении ее подсистем - Солнца и планет) площади, описываемые радиусами-векторами планет (в гелиоцентрической системе координат), сохраняются постоянными.

Инварианты определяются физическим содержанием, устройством и ресурсом системы, а не целевой функцией. Например, инвариантом производственного комплекса не является количество выпускаемой продукции, которая существенно зависит от окружающей среды: при отсутствии сырья выпуск продукции невозможен. Инвариантом производственного комплекса является его энергоинформационный ресурс.

Автономные законы сохранения сложных систем имеют модельный характер, они действенны постольку, поскольку модель адекватна системе. В этом их особенность и отличие от естественнонаучных законов.

Лингвистическое определение постулата автономности. Сложные системы имеют автономную пространственно-временную метрику (группу преобразований) и внутрисистемные законы сохранения, определяемые физическим содержанием и устройством системы и не зависящие от внешней среды.

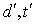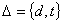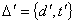Математическое определение постулата автономности. Обозначим расстояние и время в среде C через d, t, в системе S через , пары и - метрики среды и системы; скорости протекания аналогичных процессов соответственно ;
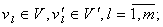при 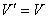имеем ;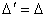
множество видов взаимодействия в системе ;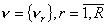
множество инвариантов системы ;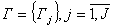
множество величин, относительно которых действуют законы сохранения, .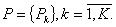

Тогда

.

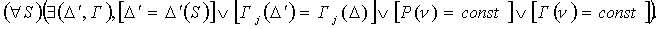Это читается так: "для всех сложных систем S существуют пространственно-временная метрика 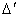и множество инвариантов Г, такие, что пара 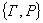определяется устройством системы и при любых возможных видах внутрисистемного взаимодействия она постоянна и не зависит от метрики".

Дата добавления: 2014-01-11