Частотный критерий Котельникова

Квантование по времени.

При квантовании по времени непрерывная по аргументу функция x(t) описывающая сигнал, преобразуется в функцию x_д(t) дискретного аргумента. Такое преобразование может быть выполнено путем взятия отсчетов функции x(t) в определенные дискретные моменты времени t₀ t₁ t₂ .. t_n. В результате функция x(t) заменяется совокупностью мгновенных значений x(t_i) i = 0..n.

Временной интервал T_k = t_i - t_i-1 между двумя соседними фиксированными моментами времени, в которых задается дискретная функция называется интервал временного квантования.

F_k = 1/T_k (1) частота квантования.

По мгновенным значениям x(t_i) можно восстановить исходную функцию с определенной точностью. Функцию полученную в результате восстановления по отсчетам x(t_i), называют воспроизводящей. Очевидно, что с понижением T_k воспроизводящая функция будет с большей точностью отображать исходную x(t).

Квантование сигналов по времени может быть равномерным и неравномерным.

При равномерном квантовании функции x(t) интервал T_k = const. Его величина выбирается на основе априорных сведений о сигнале.

При неравномерном квантовании величина T_k изменяется с учетом изменения характеристик сигнала (адаптивное квантование). Данное квантование реализуется сложнее, однако снижает избыточность отсчетов. Известно несколько критериев выбора T_k.

Данный критерий основывается на следующей модели сигнала:

· Сигнал представляет собой стационарный случайный процесс

· Спектр сигнала сплошной и ограничен некоторой частотой за пределами которой он тождественно равен нулю.

Теорема Котельникова.: если непрерывная функция x(t) удовлетворяет условиям Дирихле (ограничена, кусочно-непрерывна и имеет конечное число экстремумов) и ее спект ограничен некоторой частотой f_c, то она полностью определяется последовательностью своих значений в точках, отстоящих на расстоянии T_k = 1/2 f_c друг от друга.

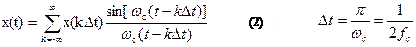Аналитически теорема Котельникова выражается рядом

Т.е. непрерывная функция разлагается в виде суммы каждый член которой выражается одинаковой функцией - произведением функций вида sin y/y (функции отсчета) и коэффициента x(kDt), определяющего значения функции x(t) в моменты отсчета. Функция отсчета sin y/y представлена графически на рис 1. Эта функция в момент времени t = kDt достигает максимального значения и равна единице. В момент времени t = (k + i)Dt, где i =1..¥ функция отсчета обращается в изм.

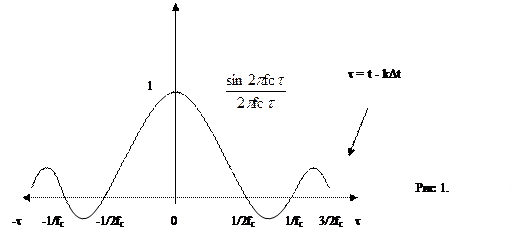
Известно что функция вида siny/y представляет собой реакцию идеального фильтра НЧ с граничной частотой v_c =2pf_c на дельта функцию (единичный импульс) откуда следует, если пропустить квантованный по времени сигнал с частотой квантования f_k =2f_c = v_c/p через такой фильтр НЧ, то суммируя выходные сигналы фильтра можно получить исходный непрерывный сигнал x(t).

Недостатки использования частотного критерия Котельникова:

· Согласно выражению (2) суммирование производится от -¥ до ¥.

· Функция отсчета (см рис 1.) должны иметь бесконечную протяженность во времени как для положительных значений t так и для отрицательных.

· Сигналы на практике ограничены по времени и бесконечны по спектру.

Поэтому с целью использования теоремы Котельникова для квантования сигналов реальный спектр сигнала простирающийся от нулю до ¥ условно ограничивают диапазоном частот от 0 до v_c, в котором сосредоточена основная часть энергии спектра (рис2.).

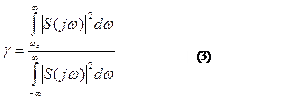Энергия отсекаемой части спектра характеризует погрешность возникающую за счет ограничений спектра частотой w_C. Эту погрешность оценивают отношением энергии содержащейся в отсекаемой части спектра к общей энергии сигнала.

Погрешность удобно оценивать следующим выражением

X_max, X_min - предельные значения функции x(t);

T - длительность сигнала;

D_wc - дисперсия приведенной погрешности.

Дата добавления: 2014-01-13