Квантование по уровню. Ошибки квантования по уровню

При квантовании по уровню непрерывное множество значений функции x(t) заменяется множеством дискретных значений. Для этого в диапазоне непрерывных значений функции

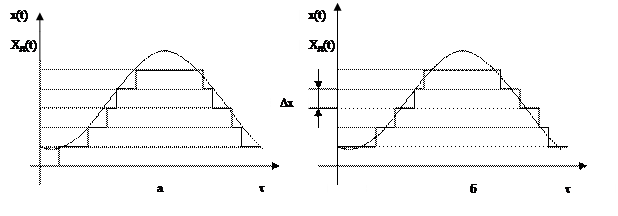
x(t) выбирается конечное число дискретных значений. В процессе квантования значения функции x(t) в любой момент времени заменяется ближайшим дискретным значением. В результате образуется ступенчатая функция x_д(t).

Квантование по уровню практически может осуществляться двумя способами (см рис.3). При первом способе мгновенное значение функции x(t) заменяется меньшим дискретным значением (рис а). При втором способе квантования мгновенное значение функции x(t) заменяется ближайшим менишим или большим дискретным значением в зависимости от того какое ближе расположению. В этом случае переход ступенчатой функции с одной ступени на другую происходит в те моменты, когда начальная непрерывная функция x(t) пересекает середину между соседними дискретными уровнями (рис б).

Расстояния между соседними уровнями - шаг квантования (стр 77-78).

Различают равномерное квантование по уровню, при котором шаг квантования постоянен, и неравномерное квантование по уровню - шаг квантования непостоянен. Получило распростанение равномерное квантование из-за простоты технической реализации.

Квантование сигнала по уровню осуществляется с помощью нелинейного элемента квантизатора (рис 4.), амплитудная характеристика которого определяется способом квантования.

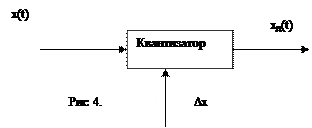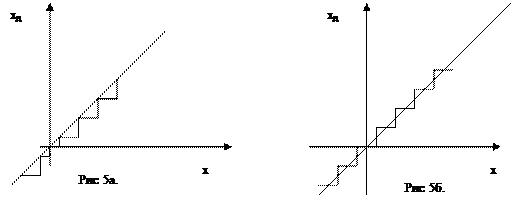
На рис 5а. Показана характеристика квантизатора при квантовании способом замены случайной величины x(t) ближайшим меньшим дискретным значением. Характеристика на рис 5б соответствует способу квантования заменой случайной величины x(t) ближайшим меньшим или большим дискретным значением.

При квантовании сигнала по уровню появляются методические погрешности, так как действительное мгновенное значение функции заменяется дискретным. Эта погрешность имеет случайный характер. Абсолютное ее значение в любой момент времени определяется формулой:

d_к(t) = x_д(t) - x(t)

где x_д(t) квантованное значение, x(t) - действительное мгновенное.

Для различных способов квантования d_к(t) имеет следующий вид.

Закон распределения погрешности зависит от закона распределения x(t).

При использовании первого способа квантования с достаточно большим числом уровней плотность вероятностей распределения погрешностей квантования определяется

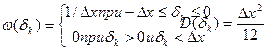
Тогда математическое ожидание и дисперсия погрешности квантования

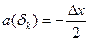
При квантовании векторным способом плотность вероятностей распределения погрешностей квантования

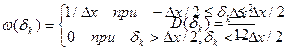
Соответственно математическое ожидание и дисперсия

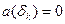
Дата добавления: 2014-01-13