Информационные пределы избыточности

Основные понятия и определения. Цель кодирования.

Учебные вопросы занятия

Лекция № 6 Кодирование информации

ЛЕКЦИЯ

Защиты информации

по учебной дисциплине "Теория информации "

для студентов специальности 075500 (090105) – Комплексное обеспечение информационной безопасности автоматизированных систем

Ставрополь 2009 г.

Цель занятия: Изучить основные понятия и определения теории кодирования. Ознакомиться с целью кодирования. Изучить классификацию помехоустойчивых кодов. Ознакомиться с корректирующими способностями кодов.

1. Основные понятия и определения. Цель кодирования

2. Информационные пределы избыточности

3. Построение безизбыточных кодов

Преобразование сообщения в сигнал называется кодированием. Пусть существует источник информации, который выдает некоторые сообщения, которые можно представить как последовательность элементарных сообщений эти элементарные сообщения называются символами сообщения, а их совокупность образует алфавит источника ({A_i}).

Кодирование сводится к замене последовательности символов источника на последовательность кодовых комбинаций.

Цель кодирования - представить сообщение в форме, которая обеспечивала бы простоту и эффективность обработки; обеспечить наилучешее сопряжение свойств источника сообщения со свойствами канала; обеспечить требуемую достоверность передачи информации в условиях помех. При этом кодирование обеспечивая достоверность передачи не должно изменять количество информации в сообщении.

Классификация кодовых конструкций.

По условиям построения кодовых конструкций:

· Равномерное

· Неравномерное

В равномерном сообщении сообщения передаются кодовыми группами с одним числом элементов. N=const

В неравномерном разные сообщения передаются кодовыми группами различной длины N¹const (азбука Морзе).

(-) неравномерные коды не обладают свойством помехозащищенности

(+) неравномерные коды обеспечивают максимальное быстродействие и минимум избыточности

(+) равномерные коды обладают потенциальной помехоустойчивостью

(-) в равномерных кодах присутствует избыточность, т.е. меньше быстродействие

По форме представления кодов:

· Последовательные - элементы кода посылаются последовательно во времени

(+) минимум аппаратных затрат

(-) потери во времени

· Параллельные - элементарные символы идут в канал одновременно.

По возможности обнаружения и исправления ошибок:

· Простые. Ошибка приводит к появлению разрешенной кодовой комбинации.

· Корректирующие. Ошибка обнаруживается и исправляется.

По законам кодообразования:

· Комбинаторные (нечисловые). Строятся по законам теории соединения (сочетания).

· Арифметические (числовые). Строятся по основным законам математической логики.

Как отмечалось выше, средняя энтропия источника сообщений может быть различной в зависимости от статистических характеристик элементов сообщения. Энтропия максимальна и определяется выражением

I(X) = log₂ M

если элементы сообщений являются равновероятными и взаимно независимыми. Если поступление элементов сообщений не равновероятно, то энтропия в этом случае определяется выражением (2).

Еще меньшей будет энтропия при наличии коррелятивных связей между элементами сообщений (см. неравенство 3). Причем энтропия уменьшается при усилении коррелятивных связей.

Сообщение, энтропия которых является максимальной, считается оптимальным с точки зрения передачи наибольшего количества информации.

Мерой количественной оценки того, насколько данное реальное сообщение по своей энтропии отличается от соответствующего ему оптимального сообщения, является коэффициент сжатия

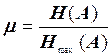(4)

где Н(А) – реальная энтропия, Н_мах(А) – максимальная энтропия.

Если неоптимальное и оптимальное сообщения характеризуются одинаковой энтропией, то справедливо равенство

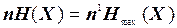(5)

где n, n¹ – число разрядов неоптимального и оптимального сообщений соответственно.

При этом число разрядов неоптимального сообщения всегда будет больше числа разрядов оптимального. Таким образом, коэффициент сжатия можно выразить

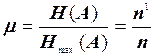(6)

Другой информационной характеристикой, являющейся мерой информационного предела избыточности, является коэффициент избыточности

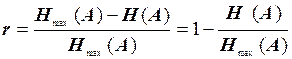(7).

Избыточность источника зависит как от протяженности статистических связей между последовательно выбираемыми элементами, так и от степени неравновероятности отдельных элементов. Если источник «без памяти», то последовательно передаваемые элементы являются независимыми, и все элементы – равновероятны, то коэффициент избыточности равен нулю.

Избыточность приводит к увеличению времени передачи сообщений, излишней загрузке канала связи. Однако не всегда надо стремиться избавиться от избыточности. Некоторая избыточность вводится специально, чтобы обеспечить требуемую достоверность передачи информации по каналу связи с помехами (избыточное помехоустойчивое кодирование).

3. Построение безизбыточных кодов

Составные коды базируются на составных системах счисления и имеют как правило два и более основания. При таком кодировании числа заданные в системе с некоторым основанием q изображаются с помощью цифр другой системы с основанием p<q. Среди составных кодов наибольшее применение получили двоично-десятичные коды. Такие коды используют в качестве промежуточных при переводе из двоичной в десятичную систему счисления. Каждая цифра десятичного кода представляется в виде четырех цифр двоичного кода. 75 0111 0101

Для фиксированных цифр десятичного числа получили распространение следующие составные коды: 8-4-2-1 7-4-2-1 2-4-2-1

Так как вместо шестнадцати цифр используется только десять - помехоустойчивость.

Рефлексные - отраженные. В простейших кодах при переходе от младших к старшим могут изменяться сразу несколько разрядов

0111 = 7

1

1001 = 8

может являться источником ошибок в некоторых способах кодирования. Для устранения этого явления используются специальные двоичные коды, в которых переход от одного изображения соседних чисел изменяют лишь значение одной цифры. В результате погрешность за счет неоднозначности считывания не превышает единицы изображаемого числа. Таким кодом является код Грея.

	Двоичное	Код Грея

Помехоустойчивое кодирование строится на теории Шенона для канала с помехами. Суть в следующем: для облегчения декодирования в канале с помехами со сколь угодно малой величиной вероятности ошибки необходимо использовать избыточность символов. Введение избыточности осуществляется с определенными правилами, такими что проверка кодовых конструкций на приемной стороне позволила бы обнаружить и исправить ошибки. Помехоустойчивым называется код, который позволяет обнаруживать и исправлять ошибки возникающие при передаче по каналу из за возникновения помех.

Дата добавления: 2014-01-13