Основные направления каллиграфической работы по годам обучения

Особенности построения узлов цифровых устройств на микросхемах

План лекции

№ п/п	Учебные вопросы	Время, мин.
1. 2.     3.	ВВОДНАЯ ЧАСТЬ ОСНОВНАЯ ЧАСТЬ 1. Особенности построения узлов цифровых устройств на микросхемах. 2. Методы синтеза комбинационных и последователь - ностных схем.   ЗАКЛЮЧИТЕЛЬНАЯ ЧАСТЬ

Материальное обеспечение:

1. Плакат "Основы алгебры Буля".

2. Демонстрационный комплекс, набор слайдов.

Литература.

1. Калабеков Б.А. Цифровые устройства и микропроцессорные системы.- М.Горячая линия – Телеком, 2000г., с.34-44.

ВВОДНАЯ ЧАСТЬ

На предыдущей лекции рассмотрены способы задания булевых функций: на словах, табличный, алгебраический и цифровой. Во всех случаях булева функция должна отражать логику работы цифрового устройства. По известной булевой функции можно построить схему цифрового устройства. Применение булевой алгебры позволяет не только построить схему, но и оптимизировать ее по числу использованных элементов. Все эти важные для практики вопросы будут рассмотрены в данной лекции.

ОСНОВНАЯ ЧАСТЬ

В настоящее время любые цифровые устройства строятся на интегральных микросхемах. Микросхемы выпускаются сериями. Серия представляет собой набор микросхем разного функционального назначения, предназначенных для совместного применения в аппаратуре. Применение микросхем одной серии позволяет более эффективно решить задачу стандартизации и унификации элементной базы. С другой стороны, построение аппаратуры техники связи на цифровых интегральных схемах уменьшает число внешних соединений и повышает за счет этого надежность, уменьшает энергопотребление, снижает стоимость, существенно улучшает габаритно-весовые показатели устройств.

При выборе серии микросхем для проектируемой схемы следует сравнить требования, предъявляемые к ней с возможностью микросхем, для характеристики которых используются следующие параметры:

U_ип – напряжение источника питания;

U⁰_вых, U¹_вых – выходное напряжение 0 и 1;

I⁰_вх,I¹_вх,I⁰_вых,I¹_вых – входные и выходные токи;

Р_потр – потребляемая мощность;

t_зд – время задержки прохождения сигнала и др.

Одним из основных параметров, определяющих область применения микросхем, является быстродействие. По быстродействию цифровые схемы делятся на три группы:

высокого быстродействия t_зд £ 10 нс;

среднего быстродействия t_зд £ 50 нс;

низкого быстродействия t_зд ³ 50 нс.

По принципу построения цифровые микросхемы подразделяются на следующие классы:

эмиттерно-связной логики (ЭСЛ);

транзисторно-транзисторной логики (ТТЛ);

интегральной инжекционной логики (ИИЛ);

логики на МДП-транзисторах (КМДП).

Серии микросхем принято характеризовать параметрами базового логического элемента, на основе которого построены все микросхемы серии.

Основным базовым элементов микросхем эмиттерно-связной логики является токовый переключатель на двух биполярных транзисторах. В интегральной инжекционной логике таким элементом является транзисторный ключ с инжекционным питанием со стороны эмиттера. В транзисторно-транзисторной логике – многоэмиттерный транзистор со сложным эмиттерным повторителем на выходе, а в логике на МДП-транзисторах – ключ на комплементарных полевых транзисторах (ключ на двух полевых транзисторах с каналами различной проводимости).

Наиболее распространенные серии микросхем и их основные параметры приведены в табл.1.

Таблица 1

Тип	Серии	tзд нс	Рпотр мвт
ЭСЛ	100, 500, 1500, 6500, 1543, 1590	1 - 3	20 -30
ТТЛ	130, 131, 133, 155, 134, 136, 158	5 –100
ТТЛШ	530, 531, 533, 555, 1530,1531,1533	3 –10
КМДП	176, 561, 564, 1561, 1564		10^- 3

Цифровая микросхема представляет собой пластмассовый корпус прямоугольной формы с пластинчатыми выводами, расположенными вдоль длинных сторон корпуса. Сверху на корпусе имеется маркировочная надпись типа микросхемы и изображается небольшая круглая метка, от которой ведется нумерация выводов. Если смотреть на микросхему снизу, то номер вывода определяется от метки по движению часовой стрелки, а если сверху – то против часовой стрелки.

На рис.1 приведен рисунок внешнего вида микросхемы К155ЛА3 и ее условное графическое обозначение. Данная микросхема состоит из четырех логических элементов 2И – НЕ, питающихся от общего источника постоянного тока напряжением 5В. Нахождение элемента в корпусе определяется по номерам выводов, поставленных на условном графическом обозначении. Так входы первого элемента находятся на выводах 1 и 2, а выход – на выводе 3. Второй элемент имеет входы на 4 и 5 выводах, а выход – на 6 и т.д.

Выводы 7 и 14 предназначены для подачи питания на все элементы, причем 14 вывод соединяется с плюсом источника, а 7 – с минусом, который чаще всего соединяется с корпусом. На условном графическом обозначении эти выводы не изображаются потому, что элементы микросхемы могут изображаться раздельно, в различных участках схемы. Цепи же питания элементов остаются общими и будут только затруднять чтение схемы.

На рис.2а показана схема устройства сложения по модулю два, выполненная на одном корпусе микросхемы к155ЛА3. На том же рисунке (рис.2б) приведен внешний вид данной микросхемы и показаны соединения в соответствии со схемой. Входами схемы являются выводы 1 и 2 элемента D1.1, соединенные одновременно с 4 выводом элемента D1.2 и 10 – элемента D1.3. Выход элемента D1.1 (вывод 3) соединяется с 5 выводом (вторым входом элемента D1.2) и 9 выводом (вторым входом элемента D1.3). Выходы элементов D1.2 и D1.3 соединяются с 12 и 13 выводами, которые являются входами элемента D1.4. Выходом схемы является выход элемента D1.4 или 11 вывод микросхемы. Плюс источника 5В подключается к выводу 14, а вывод 7 соединяется с корпусом и является общим проводом для входов и выхода приведенной схемы.

Таким образом, в данном вопросе рассмотрены особенности цифровых микросхем и пример построения схемы цифрового устройства.

2. Методы синтеза комбинационных и последовательностных схем

Применение алгебры Буля наиболее эффективной оказалось при решении задач синтеза комбинационных цифровых устройств. В большинстве случаев в ходе решения таких задач можно выделить следующие этапы:

1. Задание булевой функции устройства на словах.

2. Составление таблицы истинности - табличное задание булевой функции.

3. Запись алгебраического выражения булевой функции.

4. Минимизация полученного выражения булевой функции.

5. Построение по минимизированной булевой функции схемы цифрового устройства.

Сущность первых трех этапов уже рассматривалась в ходе прошлой лекции, поэтому более детально остановимся именно на четвертом и пятом этапах.

Основная задача этапа минимизации состоит в получении минимальной формы булевой функции, т.е. такой формы, которой соответствует логическая схема с минимальным числом элементов и минимальным числом входов этих элементов. В основе минимизации булевых функций лежат законы склеивания и поглощения. Однако применение этих законов на практике требует определенных навыков, что связано с большими затратами времени.

Одним из способов, позволяющих формализовать процедуру минимизации, является применение так называемых диаграмм или карт Карно. Карта Карно представляет собой прямоугольник, разбитый на квадраты, число которых равно общему числу наборов для данной функции n переменных, т.е. оно равно 2ⁿ. Так, для функции трех переменных квадратов будет 8, для четырех переменных - 16 и т.д. Каждый квадрат соответствует определенному набору. Для примера рассмотрим карту Карно для четырех переменных (рис.3а).

A

B

ABCD

ABCD

ABCD

ABCD

ABCD

ABCD

ABCD

ABCD

ABCD

ABCD

ABCD

ABCD

ABCD

ABCD

ABCD

ABCD

D

а) С б)

Рис.3

Однако для работы удобнее использовать карту, приведенную на рис.3б. Иногда в углу квадратов ставят номер набора, что облегчает процесс минимизации при задании булевой функции числовым способом.

Рекомендуется минимизацию исходного выражения булевой функции производить в следующей последовательности:

1. Вычертить карту Карно.

2. Нанести булеву функцию на карту - поставить 1 в квадраты, соответствующие тем набором, на которых функция равна единице.

3. Произвести объединение соседних единиц. В одно объединение могут входить 8 или 4 или 2 единицы. Причем, соседними считаются не только единицы, находящиеся в соседних квадратах, но и расположенные по концам строки или столбца.

4. Записать минимизированное выражение булевой функции с учетом следующих правил:

а) если единицами заполнены две соседние строки или два соседних столбца, то они заменяются одной переменной, которая является общей для них;

б) если единицами заполнена одна строка или столбец или квадрат, то они заменяются двумя переменными общими для них;

в) если единицы расположены в двух соседних квадратах, в том числе на концах строки или столбца, то они заменяются тремя переменными общими для них;

г) если единица не вошла ни в одно из объединений, то соответствующий ей набор записывается в исходном виде.

При объединении необходимо учитывать, что одна и та же единица может входить в любое число объединений, а начинать объединять единиц надо с максимально возможного их числа.

Проиллюстрируем применение карты Карно на примере. Пусть задана булева функция четырех переменных

F(A,B,C,D) = 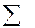(0, 3, 4, 5, 7, 8, 10, 11, 14, 15).

Вычертим карту Карно для четырех переменных и нанесем не нее булеву функцию (рис.4)

A

B

D

Ф

Ф

С Рис.4

Проведем объединение единиц как показано на карте. В результате получаем:

F = AC + CD + BCD + ABC.

Эффективность минимизации видна из сравнения полученной булевой функции с исходной.

Положительный эффект минимизации удается еще больше усилить, если в результате анализа условий работы цифрового устройства удается установить, что некоторые комбинации входных переменных в процессе работы никогда не будут встречаться. Следовательно, булеву функцию на этих наборах можно доопределить произвольно по своему усмотрению. Такие наборы называют факультативными.

Если в рассматриваемом примере предположить, что факультативными являются 2 и 6 наборы, то с учетом факультативных наборов минимизированное выражение будет

F = C + AB + BD.

Итак, применение карт Карно в процессе решения задач синтеза комбинационных цифровых устройств позволяет найти оптимальное решение. При решении задачи синтеза последовательностных устройств данную методику можно применить при разработке комбинационной части устройства.

По полученному минимизированному выражению булевой функции используя логические элементы И, ИЛИ, НЕ, можно построить схему, иначе говоря, реализовать заданную булеву функцию.

Логические элементы, предназначенные для выполнения указанных в формуле операций, располагаются в схеме, начиная от входов, в таком же порядке, в каком выполняются логические операции. В начале изображаются инверторы для получения входных переменных с отрицаниями, затем элементы И, потом элемент ИЛИ.

Пусть устройство с двумя входами и одним выходом имеет булеву функцию

,

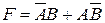тогда воспользовавшись изложенными выше рекомендациями, его схему можно представить следующим образом (рис.5)

Совокупность элементов, позволяющая строить на их базе логическую схему любой сложности, называется функционально полной системой элементов. Следовательно, совокупность элементов И, ИЛИ, НЕ является функционально полной системой. Однако существуют и другие функционально полные системы, включающие в себя меньшее число элементов. Такими системами являются:

1. Система из элементов ИЛИ, НЕ;

2. Система из элементов И, НЕ;

3. Система из одного элемента ИЛИ-НЕ;

4. Система из одного элемента И-НЕ.

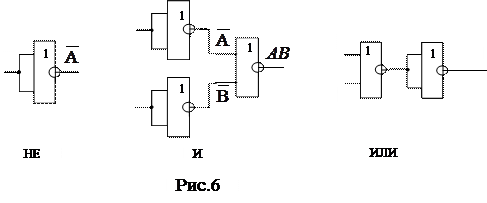Особый интерес на практике представляют две последние системы. Действительно, с помощью элемента ИЛИ-НЕ можно реализовать все логические операции (рис.6)

Нетрудно показать, что и с помощью элемента И-НЕ также можно реализовать все три логические операции.

ЗАКЛЮЧИТЕЛЬНАЯ ЧАСТЬ

Таким образом, в ходе данной лекции показаны замечательные свойства аппарата булевой алгебры в решении задач синтеза комбинационных логических схем. На закрепление данных вопросов направлена курсовая работа, которая будет выполняться в следующем семестре. Первичные навыки в минимизации логических схем вам будут даны в ходе четырехчасового практического занятия.

Задание на самостоятельную работу

1.Изучить материал по учебнику [1] страницы 34-44.

2.Решить задачу: минимизировать с применением карты Карно булеву функцию четырех переменных,. если она задана в цифровом виде

F (A,B,C,D) =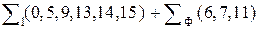

Доцент кафедры Б.Степанов

Рецензент начальник кафедры

полковник Г.Журбин

По окончании периода обучения грамоте начинается систематическая выработка графического навыка и формирование индивидуального каллиграфического почерка у учащихся на уроках русского языка...

Согласно требованиям программы по русскому языку ежедневно на уроках планируются специальные занятия чистописанием по 3-5 минут, так называемые «каллиграфические минутки». Цель занятий состоит в том, чтобы укрепить приобретенные умения писать чисто, правильно, разборчиво буквы и их соединения, слова и предложения, добиться ускорения темпа, связности, ритмичности письма. Учителю следует продолжать следить за посадкой, за правильным положением тетради, ручки, а также за тем, чтобы буквы были определенной высоты, правильного наклона, чтобы расстояние между буквами и словами было одинаковым.

Образцы красивого и правильного письма учитель ежедневно прописывает в тетрадях учащихся и на классной доске.

В методике обучения чистописанию традиционно используется генетический принцип группировки письменных букв, в соответствии с которым все буквы письменного алфавита объединены в группы, которые включают сходные по начертанию элементы, начиная с простейших.

Работа над формой букв и их элементов проводится в порядке возрастающей трудности их написания. Сначала дети упражняются в написании малых, а затем больших букв.

Дата добавления: 2014-01-11