Метод точечных источников тепла. Выравнивание температуры в неограниченном стержне

Функцию G(x,x,t) называют фундаментальным решением уравнения теплопроводности. Это связано с тем, что с помощью него можно сконструировать решения уравнения теплопроводности для различных краевых условий. Для этого процесс распространения тепла в твердом теле теплопроводностью необходимо представить как совокупность процессов выравнивания температуры от множества элементарных точечных источников тепла. Этот прием называется методом точечных источников тепла.

Для решения дифференциального уравнения теплопроводности (1.12) задают краевые условия, включающие начальные и граничные условия. Начальное условие задает распределение температуры внутри тела (для одномерного поля – в стержне) в начальный момент времени:

, (1.15)

где f(x) – известная функция (рис. 1.3).

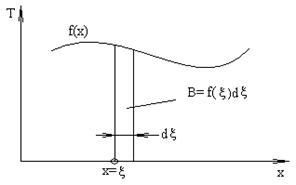
Рис. 1.3. Схема представления начального распределения температуры стержня совокупностью элементарных точечных источников теплоты

Важным частным случаем является равномерное распределение температуры в начальный момент времени:

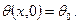
Граничные условия задают различными способами. В частности, один из способов, называемых граничными условиями первого рода, состоит в задании распределения температуры на поверхности тела (например, на торце стержня) в любой момент времени [3]:

(1.16)

Важным частным случаем является задание постоянной температуры:

(1.17)

Воспользуемся идеей метода точечных источников тепла для описания процесса выравнивания температуры в неограниченном стержне. Представим начальные условия, заданные в виде известной функции как суммы бесконечного множества кривых вида [3]:

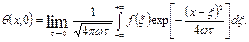(1.18)

Нетрудно убедиться в том, что функция

(1.19)

удовлетворяет уравнению теплопроводности (1.12) и начальным условиям (1.18) и, следовательно, является решением для выравнивания температуры в неограниченном стержне от заданного распределения температуры в начальный момент времени.

Дата добавления: 2014-01-13