Силы при фрезеровании цилиндрическими фрезами

Схема и расчет сил при свободном косоугольном точении

Схема и расчет сил при свободном прямоугольном точении

Методика расчета сил резания в каждом конкретном случае должна учитывать закономерности и специфику рассматриваемого способа обработки. По числу, форме и расположению режущих кромок точение может представлять собой одну из четырех разновидностей лезвийной обработки: свободное прямоугольное, несвободное прямоугольное, свободное косоугольное и несвободное косоугольное резания. Каждая из названных схем имеет свои особенности, которые проявляются, главным образом, в положении плоскости стружкообразования относительно системы технологических координат x, y, z.

Наиболее простым является случай свободного прямоугольного резания, когда резание осуществляется одной прямолинейной кромкой, перпендикулярной к скорости резания v (рис. 2.18)

При свободном прямоугольном точении плоскость стружкообразования перпендикулярна режущей кромке, т. е. совпадает с главной секущей плоскостью, и содержит векторы скоростей схода стружки v ₁и резания v. Введем систему координат n, m, x,связанную с плоскостью стружкообразования (рис. 2.19).

Ось n совпадает с проекцией вектора скорости схода стружки на основную плоскость, а ось x – с вектором скорости резания. При этом третья ось координат m направлена вдоль режущей кромки резца. Силы на задней поверхности (F ₁ и N ₁), определяющиеся в главной секущей плоскости (рис. 2.19, б), и проекции силы стружкообразования (R _n и R _x), определяющиеся в плоскости стружкообразования, в данном случае находятся в одной плоскости. Проекция силы резания на ось m равна нулю.

.

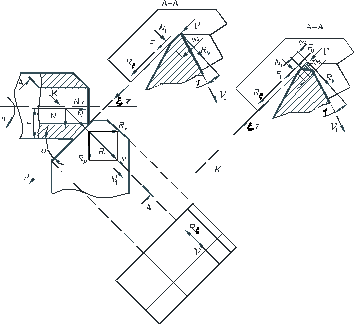
Рис. 2.19. Положение плоскости стружкообразования и схема сил при свободном прямоугольном точении: а) силы в основной плоскости; б) силы в плоскости стружкообразования; в) силы в плоскости резания; г) силы в плоскости стружкообразования

при наличии застойной зоны

При расчете сил будем исходить из того, что в плоскости стружкообразования проекции силы стружкообразования на оси n, x иm определяются одинаково для свободного прямоугольного, несвободного прямоугольного, свободного косоугольного и несвободного косоугольного резания: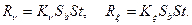

Отличия в расчетных схемах при определении проекций этих сил на технологические оси заключаются лишь в учете того факта, что в каждом из этих случаев положение плоскости стружкообразования относительно технологических осей различно.

Силы F ₁ и N ₁ на задних поверхностях инструмента, или в застойной зоне, для всех схем резания будем определять в плоскостях, перпендикулярных проекциям режущих кромок на основную плоскость.

Выразим силы N ₁ и F ₁ через нормальные напряжения q_{N 1} и коэффициент трения m₁ на задней поверхности инструмента [1]:

(2.42)

Согласно экспериментальным данным, для резания сталей на ферритной основе твердостью HB < 3000 МПа без применения смазочно-охлаждающих жидкостей можно принять

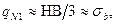
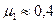. (2.43)

На задней поверхности застойной зоны, образующейся при наличии на передней поверхности инструмента упрочняющей фаски, удельные касательные силы больше, чем на фаске износа. Они могут быть ориентировочно приняты в следующем соотношении к действительному пределу прочности при растяжении:

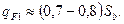(2.44)

С учетом вышеизложенного формулы для определения сил P_X, P_Y, P_Z при свободном прямоугольном точении имеют вид:

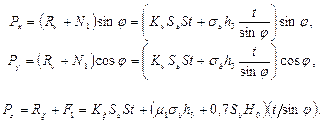(2.45)

В третьей из формул (2.45) учтена касательная сила на задней поверхности застойной зоны, высота которой равна H ₀.

При несвободном прямоугольном резании направление схода стружки n определяется с учетом формы и длин режущих кромок, участвующих в резании.

Для свободного косоугольного резания положение системы координат m, n, x зададим относительно другой системы координат m₀, n₀, x₀, справедливой для свободного прямоугольного резания (рис. 2.19).

При этом действительное положение системы координат m, n, x может быть охарактеризовано с помощью двух последовательных поворотов системы координат m₀, n₀, x₀. Первый поворот осуществляется в плоскости m₀, x₀ относительно оси n₀ на угол l. При этом новые оси m¢ и x будут составлять угол l со старыми осями m₀, x₀ (рис. 2.20).

В плоскости стружкообразования x, n известны силы R _x и R_n, которые могут быть определены по аналогии со свободным прямоугольным точением. По определению, сила R _x составляет с осью x₀ (или с технологической осью z) угол l. Однако направление силы R_n в плоскости m₀, n₀, перпендикулярной скорости резания v, неизвестно.

Для определения угла y₁ между осью y и n (см. рис. 2.20) примем допущение, что сила R_n равна R_{n 0} и направлена вдоль оси n ₀, т.е. перпендикулярно проекции режущей кромки на плоскость m₀, n₀. Проекции этой силы на технологические оси x и y соответственно будут: 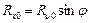и .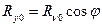

Силу R _x также разложим на две составляющие (см. рис. 2.20): 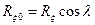и .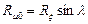

Поскольку сила R_m0 так же, как сила R_n0, находится в плоскости x, y, найдем ее проекции на технологические оси:

, .

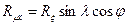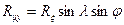Таким образом, результирующие значения проекций силы стружкообразования на технологические оси x, y определятся как:

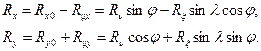(2.46)

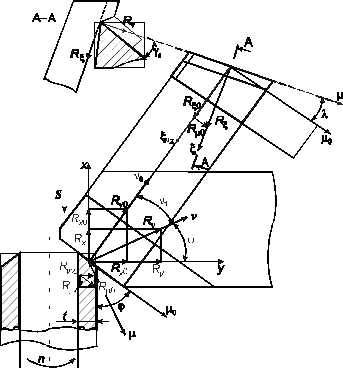
Рис. 2.20. Схема сил при свободном косоугольном продольном точении

Зная проекции силы стружкообразования на оси x и y, найдем угол y₁:

С учетом вышеизложенного, а также с учетом сил на задней поверхности режущего лезвия формулы для технологических проекций силы резания при свободном косоугольном точении примут вид:

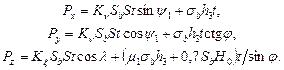(2.47)

При несвободном косоугольном резании углы отклонения стружки от нормали к режущей кромке в плоскости m₀, n₀ необходимо алгебраически складывать.

2.2.4. Силы при фрезеровании торцово‑коническими прямозубыми фрезами

Фрезерование торцовыми фрезами (торцовое фрезерование) представляет собой нестационарное несвободное резание (рис. 2.21) с круговым движением резания и любым движением подачи в плоскости, перпендикулярной оси вращения.

Как следует из вида в основной плоскости (рис. 2.21, а) и сечения в плоскости стружкообразования (рис. 2.21, в), торцовое фрезерование имеет много общего с несвободным точением.

Оно может быть как косоугольным (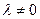), так и прямоугольным (l =0). Однако для торцовых фрез обычно применяют небольшие углы наклона зубьев. Это связано с тем, что при больших углах l создается неблагоприятная геометрия режущего лезвия на вспомогательных режущих кромках, расположенных на торце фрезы. Таким образом, влиянием угла l в этом случае оказывается возможным пренебречь с целью упрощения расчетных формул. В связи с этим ниже раcсматривается прямоугольное фрезерование.

Технологические оси при торцовом фрезеровании выбирают неподвижными относительно станка. Две оси (H и V) располагают в рабочей плоскости, причем ось H – в направленииподачи S_м, а третью ось Y – перпендикулярно рабочей плоскости.

Таким образом, при фрезеровании система координат Х, Y, Z, связанная с режущим лезвием, вращается относительно оси Y и оси X, Z изменяют свое положение относительно осей H и V.

Вследствие изменения толщины срезаемого слоя на каждом из работающих зубьев крутящий момент и мощность будут функциями угла q.

Не меньшее значение имеют изменения величины и направления сил P_H и P_V, действующих на механизмы перемещения стола фрезерного станка, а также изменения величины силы P_Y, отжимающей фрезу от обработанной поверхности детали и влияющей на точность обработки. При повороте фрезы силы P_H и P_V могут изменяться не только по величине, но и по направлению. Все это способствует возникновению вынужденных колебаний.

Для определения сил P_H и P_V, действующих в рабочей плоскости, на оси H и V проектируются силы P_zi и P_xi.

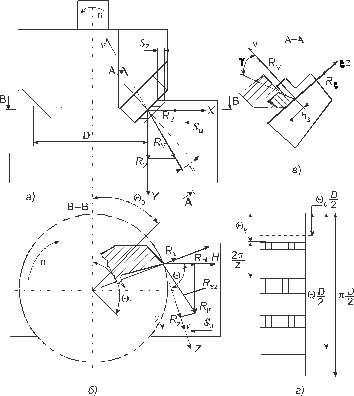
Рис. 2.21. Схема сил при несвободном прямоугольном фрезеровании торцово‑конической фрезой: а) в основной плоскости; б) в рабочей плоскости; в) в плоскости стружкообразования; г) развертка поверхности резания

Cуммируя проекции сил P_zi и P_xi на оси H и V по всем зубьям Zр, контактирующим с обрабатываемой деталью, получим:

, (2.48)

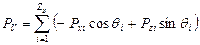. (2.49)

Анализ изменения всех составляющих силы фрезерования и крутящего момента необходим для оптимизации режимов фрезерования и конструкции фрез.

Дата добавления: 2014-01-13