Распределенного быстродвижущегося источника теплоты

Температура в полуплоскости от равномерно

ТЕПЛОФИЗИКА И ТЕРМОМЕХАНИКА РЕЗАНИЯ

Для решения многих технологических задач и, в частности, для расчета температурных полей в свариваемых деталях важное значение имеет задача о температурном поле, возникающем в полуплоскости от движущегося равномерно распределенного источника тепла (рис. 2.24).

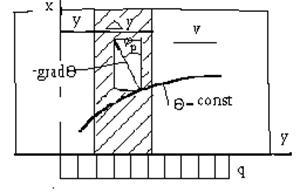
Рис. 2.24. Схема к расчету температуры в полуплоскости

от быстродвижущегося равномерно распределенного источника тепла

Значительные упрощения расчета таких температурных полей могут быть достигнуты при больших значениях критерия Pe: Ре=.

Физический смысл принимаемых при этом допущений связан с тем, что при увеличении критерия Пекле (или скорости v движущегося источника тепла) изотермы температурного поля локализуются вблизи оси y и угол наклона их к этой оси уменьшается. Соответственно нормаль к изотерме, указывающая направление теплового потока и градиента температуры, составляет с осью x малый угол j_р (рис. 2.24). Вследствие этого составляющая теплового потока вдоль оси x существенно больше, чем вдоль оси y. При достаточно больших значениях критерия Ре влиянием перетоков тепла в направлении оси y на температуру, возникающую на поверхности движущейся полуплоскости, можно пренебречь. Пренебрегая перетоками тепла вдоль оси y, элемент полуплоскости шириной Dy можно рассматривать как теплоизолированный полуограниченный стержень, к торцу которого в течение некоторого времени

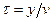(2.59)

подводится постоянный тепловой поток плотностью q, а температурное поле полуплоскости – как совокупность независимых друг от друга одномерных нестационарных процессов в стержнях.

В связи с этим рассмотрим задачу о температуре неограниченного стержня, к торцу которого подводится тепловой поток постоянной плотности.

Эта задача может быть сведена к уже известному решению задачи об одномерном нестационарном температурном поле неограниченного стержня, на торце которого поддерживается постоянная температура. С математической точки зрения эти две задачи отличаются только обозначениями. Поэтому решение для плотности тепловых потоков может быть записано в виде:

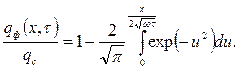(2.60)

С учетом формулы (1.4) получим [1]

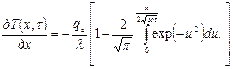
или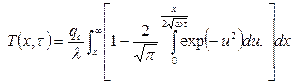. (2.61)

Из формулы (2.61), в частности, следует, что при постоянном тепловом потоке на торце стержня его температура прямо пропорциональна плотности теплового потока, обратно пропорциональна коэффициенту аккумуляции тепла и будет повышаться с течением времени пропорционально корню квадратному от времени нагрева

(2.62)

где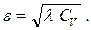

Переход от одномерной нестационарной задачи к квазистационарной двухмерной осуществляется заменой переменной (2.59)

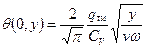. (2.63)

Как следует из (2.63), при постоянной плотности теплового потока q увеличение скорости v источника тепла приводит к уменьшению температуры.

Дата добавления: 2014-01-13