Для адиабатических условий деформации

Термомеханическое определяющее уравнение

В сравнении с различием в скоростях деформации при резании и статических механических испытаниях, составляющем 8–9 порядков, изменения скорости деформации в пределах одного порядка (или даже двух) совершенно несущественны. При допущении о постоянстве скорости деформации зависимость предела текучести от температуры и деформации может быть представлена в виде

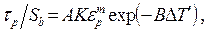(2.64)

где 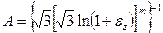, DT¢ – приращение гомологической температуры, m, k, B – показатели деформационного и скоростного упрочнения и температурного разупрочнения.

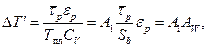
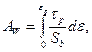(2.65)

где A_W – безразмерная удельная работа деформации.

Для решения уравнения (2.64) воспользуемся заменой переменной:

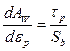. (2.66)

Интегрируя уравнение (2.64), получаем функцию, описывающую влияние истинного сдвигаe _p на удельную работу деформации A_W и на предел текучести:

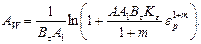(2.67)

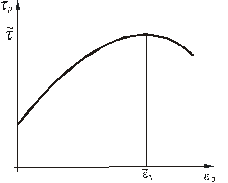Рис. 2.25. Типичная кривая зависимости предела текучести от истинного сдвига при адиабатических условиях деформации    

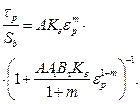(2.68)

В стационарной точке предел текучести достигает максимума

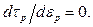(2.69)

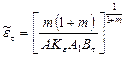
и 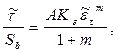(2.70)

где 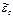, 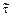– координаты стационарной точки кривой течения: локализованный сдвиг и максимальный предел текучести обрабатываемого материала при резании.

Из формулы (2.70) следует, что максимальное отношение предела текучести при резании к действительному пределу прочности при растяжении не зависит ни от режимов резания, ни от геометрических параметров инструмента. Оно определяется только измеренными при растяжении прочностными характеристиками материала, теплоемкостью и температурой плавления обрабатываемого материала, а также константами, характеризующими способность материала к скоростному упрочнению и температурному разупрочнению при резании. Это дает основание использовать максимальное значение предела текучести при резании как прочностную характеристику обрабатываемого материала в условиях резания.

Максимальный предел текучести при резании сталей приблизительно в два раза больше, чем предел текучести этого же материала при статических испытаниях. Максимальный предел текучести достигается в узкой области в окрестности режущей кромки на передней и задней поверхностях застойной зоны, а именно: в той области, где интенсивность деформаций достигает значения .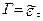

Дата добавления: 2014-01-13