О сходимости интерполяционного процесса

Возникает вопрос, будет ли стремиться к нулю погрешность интерполирования 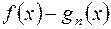, если число узлов сетки 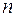неограниченно возрастает. Ответ, вообще говоря, отрицательный.

Сформулируем определение скорости сходимости интерполяционного процесса. Множество точек 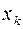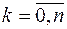, таких, что

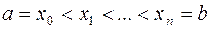
называется сеткой на отрезке 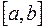и обозначается через 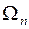. До сих пор предполагалось, что число узлов интерполяции фиксировано. Переходя к изучению сходимости, необходимо рассмотреть последовательность сеток с возрастающим числом узлов:

, ,..., ,...

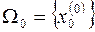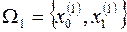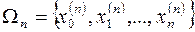Пусть функция 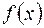определена и непрерывна на 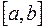. Тогда можно задать последовательность интерполяционных многочленов 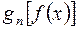, построенных для функции 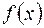по ее значениям в узлах сетки .

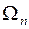Говорят, что интерполяционный процесс для функции 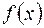сходится в точке 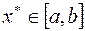, если существует

.

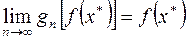Кроме поточечной сходимости рассматривается сходимость в различных нормах. Например, равномерная сходимость на отрезке 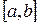означает, что

.

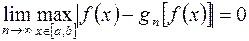Свойство сходимости или расходимости интерполяционного процесса зависит как от выбора последовательности сеток, так и от гладкости функций .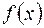

Известны примеры несложных функций, для которых интерполяционный процесс расходится. Так, последовательность интерполяционных многочленов, построенных для непрерывной функции 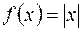по равномерноотстоящим узлам на отрезке 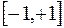, не сходится к функции 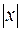ни в одной точке отрезка 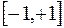, кроме точек .

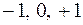С другой стороны, для заданной непрерывной функции 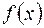можно добиться сходимости за счет выбора расположения узлов интерполяции. То есть, если 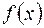непрерывна на 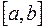, то найдется такая последовательность сеток, для которой соответствующий интерполяционный процесс сходится равномерно на .

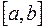Следует заметить, что построить такие сетки чрезвычайно сложно и, кроме того, для каждой функции требуется своя сетка. В практике вычислений избегают пользоваться интерполяционными многочленами высокой степени. Вместо этого применяются кусочнополиномиальная интерполяция, которая будет рассмотрена ниже.

Дата добавления: 2014-01-13