
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Численное дифференцирование
|
|
|
|
Задача численного дифференцирования состоит в приближенном вычислении производных функции 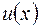 по заданным в конечном числе точек значениям этой функции. Пусть на
по заданным в конечном числе точек значениям этой функции. Пусть на  задана сетка
задана сетка
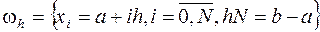
и определены значения  функции
функции 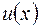 в точках сетки.
в точках сетки.
Простейшие примеры численного дифференцирования имеют вид:
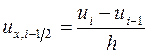 ,
, 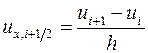 ,
, 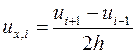
Возникающая в результате такой замены погрешность характеризуется разложениями (доказать, дом. зад. №4)
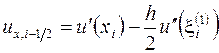 , (3.35)
, (3.35)
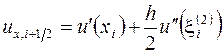 , (3.46)
, (3.46)
 , (3.37)
, (3.37)
где 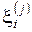 ,
,  точки из интервала
точки из интервала 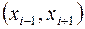 .
.
Вторую производную в точке  можно заменить отношением (доказать, дом. зад. №4)
можно заменить отношением (доказать, дом. зад. №4)
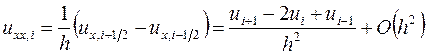 , (3.38)
, (3.38)
Третья производная в точке 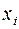 с точностью до величин
с точностью до величин 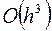 определяется по формуле (доказать, дом. зад. №4)
определяется по формуле (доказать, дом. зад. №4)
 . (3.39)
. (3.39)
Четвертая производная в точке  аппроксимируется разностным отношением (доказать, дом. зад. №4)
аппроксимируется разностным отношением (доказать, дом. зад. №4)
 .
.
Как правило, значения функции 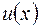 в точках сетки
в точках сетки 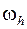 вычисляются не точно, а с каким-то приближением. Например, элементарные трансцендентные функции вычисляются с помощью рядов, причем ряды заменяются конечными суммами. Другим источником погрешностей являются погрешности округления. Оказывается, что погрешность, возникающая при вычислении разностных отношений, намного превосходит погрешность в задании значений функции
вычисляются не точно, а с каким-то приближением. Например, элементарные трансцендентные функции вычисляются с помощью рядов, причем ряды заменяются конечными суммами. Другим источником погрешностей являются погрешности округления. Оказывается, что погрешность, возникающая при вычислении разностных отношений, намного превосходит погрешность в задании значений функции 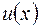 и даже может неограниченно возрастать при стремлении шага сетки
и даже может неограниченно возрастать при стремлении шага сетки 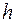 к нулю. Поэтому операцию вычисления разностных отношений называют некорректной. Поясним причину некорректости на примере вычисления разностного отношения
к нулю. Поэтому операцию вычисления разностных отношений называют некорректной. Поясним причину некорректости на примере вычисления разностного отношения 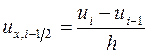 .
.
Разностное отношение  хорошо приближает
хорошо приближает 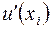 только в том случае, когда шаг
только в том случае, когда шаг 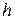 достаточно мал. Требование малости величины
достаточно мал. Требование малости величины 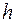 , находящейся в знаменателе разностного отношения, как раз и является причиной некорректности операции численного дифференцирования. Действительно, пусть вместо точных значений
, находящейся в знаменателе разностного отношения, как раз и является причиной некорректности операции численного дифференцирования. Действительно, пусть вместо точных значений 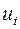 и
и 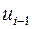 вычислены приближенные значения
вычислены приближенные значения  , и
, и 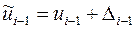 . Тогда вместо
. Тогда вместо  будет вычислена величина
будет вычислена величина  . Следовательно, погрешность в вычислении первой разностной производной окажется равной
. Следовательно, погрешность в вычислении первой разностной производной окажется равной  .
.
Пусть известна граница 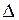 погрешностей
погрешностей  , т.е.
, т.е.  ,
,  . Тогда
. Тогда
 , (3.40)
, (3.40)
причем эта оценка достигается при 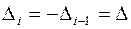 . Из оценки (3.40) видно, что вследствие малости
. Из оценки (3.40) видно, что вследствие малости 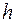 погрешность, возникающая при вычислении первой разностной производной, значительно превосходит погрешность вычисления самой функции
погрешность, возникающая при вычислении первой разностной производной, значительно превосходит погрешность вычисления самой функции 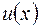 . Если
. Если 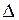 не зависит от
не зависит от 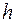 , то погрешность
, то погрешность  неограниченно возрастает при
неограниченно возрастает при 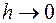 .
.
Сказанное не означает, что нельзя пользоваться формулами численного дифференцирования. Чтобы не происходило существенного понижения точности, надо следить за тем, чтобы погрешность округления имела тот же порядок, что и погрешность аппроксимации. Например, из (3.35) следует, что погрешность аппроксимации при замене 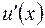 отношением
отношением  не превосходит величины
не превосходит величины 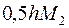 , где
, где 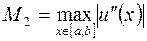 . Естественно потребовать, чтобы и погрешность округления
. Естественно потребовать, чтобы и погрешность округления  была бы сравнима с погрешностью аппроксимации, например
была бы сравнима с погрешностью аппроксимации, например
 , (3.41)
, (3.41)
где 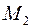 не зависит от
не зависит от 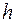 . Это означает, что погрешность
. Это означает, что погрешность 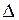 при вычислении значений функции
при вычислении значений функции 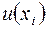 должна быть величиной
должна быть величиной 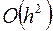 . С другой стороны, неравенство (3.41) показывает, что если величина
. С другой стороны, неравенство (3.41) показывает, что если величина 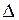 задана и мы не можем ее менять, то вычисления надо проводить не с произвольно малым шагом
задана и мы не можем ее менять, то вычисления надо проводить не с произвольно малым шагом 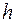 , а с шагом, удовлетворяющим условию
, а с шагом, удовлетворяющим условию 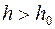 , где
, где 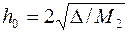 .
.
При вычислении производных более высокого порядка, когда в знаменатель разностного отношения входит  ,
, 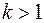 , влияние неточности в задании
, влияние неточности в задании 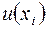 сказывается еще сильнее.
сказывается еще сильнее.
Многие формулы численного дифференцирования можно получить как следствие интерполяционных формул. Для этого достаточно заменить функцию 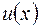 ее интерполяционным многочленом
ее интерполяционным многочленом 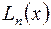 и вычислить производные многочлена
и вычислить производные многочлена 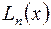 , используя его явное представление. В отличие от предыдущего, рассмотрим неравномерную сетку
, используя его явное представление. В отличие от предыдущего, рассмотрим неравномерную сетку
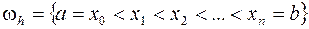
и обозначим через  ,
, 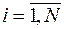 шаги этой сетки. В качестве примера получим формулы численного дифференцирования, основанные на использовании многочлена Лагранжа
шаги этой сетки. В качестве примера получим формулы численного дифференцирования, основанные на использовании многочлена Лагранжа 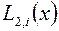 , построенного для функции
, построенного для функции 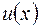 по трем точкам
по трем точкам  . Многочлен
. Многочлен 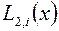 имеет вид
имеет вид
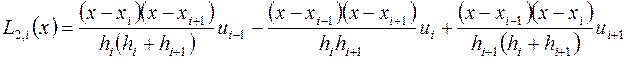 ,(3.42)
,(3.42)
отсюда получим
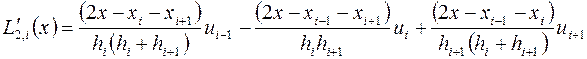
Это выражение можно принять за приближенное значение 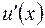 в любой точке
в любой точке  . Его удобнее записать в виде
. Его удобнее записать в виде
 , (3.43)
, (3.43)
где  . В частности, при
. В частности, при 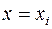 получим
получим
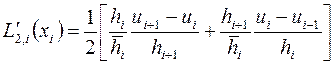 , (3.44)
, (3.44)
и если сетка равномерна, то приходим к центральной разностной производной
 .
.
Далее, вычисляя вторую производную многочлена 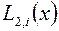 , получим приближенное выражение для
, получим приближенное выражение для  при
при  :
:
 . (3.45)
. (3.45)
На равномерной сетке это выражение совпадает со второй разностной производной 
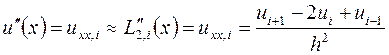 .
.
Для приближенного вычисления дальнейших производных уже недостаточно многочлена 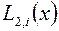 , надо привлекать многочлены более высокого порядка и тем самым увеличивать число узлов, участвующих в аппроксимации.
, надо привлекать многочлены более высокого порядка и тем самым увеличивать число узлов, участвующих в аппроксимации.
Порядок погрешности аппроксимации зависит как от порядка интерполяционного многочлена, так и от расположения узлов интерполирования. Получим выражение для погрешности аппроксимации, возникающей при замене 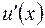 выражением
выражением 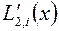 . Будем считать, что
. Будем считать, что  и что величины
и что величины  имеют один и тот же порядок малости при измельчении сетки. По формуле Тейлора в предположении ограниченности
имеют один и тот же порядок малости при измельчении сетки. По формуле Тейлора в предположении ограниченности  получим
получим
 ,
,
где 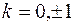 ,
,  . Отсюда приходим к следующим разложениям разностных отношений (доказать, дом. зад. №4):
. Отсюда приходим к следующим разложениям разностных отношений (доказать, дом. зад. №4):
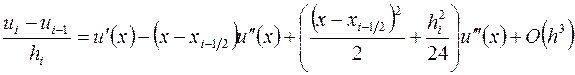 ,(3.46)
,(3.46)
 ,(3.47)
,(3.47)
где  Подставляя (3.46) и (3.47) в выражение для разностной производной (3.43) и приводя подобные члены, получим (доказать, дом. зад. №4):
Подставляя (3.46) и (3.47) в выражение для разностной производной (3.43) и приводя подобные члены, получим (доказать, дом. зад. №4):
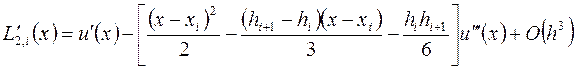 ,
, 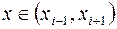 .
.
Отсюда видно, что разностное выражение (3.43) аппроксимирует 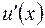 со вторым порядком. Несколько хуже обстоит дело с выражением (3.45), аппроксимирующим вторую производную. Из (3.38) видно, что на равномерной сетке в точке
со вторым порядком. Несколько хуже обстоит дело с выражением (3.45), аппроксимирующим вторую производную. Из (3.38) видно, что на равномерной сетке в точке 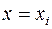 имеет место аппроксимация
имеет место аппроксимация 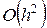 . Покажем, что на неравномерной сетке
. Покажем, что на неравномерной сетке 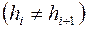 погрешность аппроксимации будет иметь только первый порядок. Подставляя разложения (3.46) и (3.47) в выражение (3.45) для
погрешность аппроксимации будет иметь только первый порядок. Подставляя разложения (3.46) и (3.47) в выражение (3.45) для 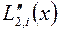 получим (доказать, дом. зад. №4):
получим (доказать, дом. зад. №4):
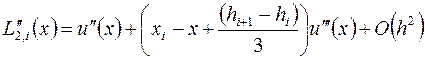 ,
, 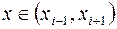 .
.
На равномерной сетке второй порядок аппроксимации имеет место лишь в точке 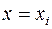 , а относительно других точек (например, точек
, а относительно других точек (например, точек  и
и 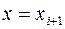 ) выполняется аппроксимация только первого порядка.
) выполняется аппроксимация только первого порядка.
|
|
|
|
|
Дата добавления: 2014-01-13; Просмотров: 1801; Нарушение авторских прав?; Мы поможем в написании вашей работы!