Общая формулировка методов. Семейство методов второго порядка

Методы Рунге-Кутта

Рассмотрим задачу Коши для одного уравнения

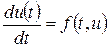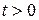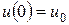, . . (8.12)

Явный 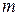-этапный метод Рунге-Кутта состоит в следующем. Пусть решение 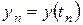уже известно. Задаются числовые коэффициенты 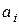, , 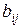, , 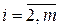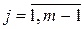и последовательно вычисляются функции

, ,

,

...

.

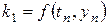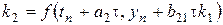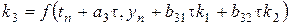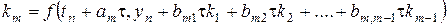Затем из формулы

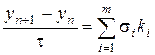(8.13)

находится новое значение .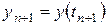

Коэффициенты 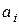, , 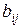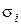выбираются из соображений точности. Например, для того чтобы уравнение (8.13) аппроксимировало исходное уравнение (8.12), как будет показано ниже, необходимо потребовать .

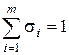Отметим, что методы Рунге-Кутта при 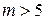не используются.

Остановимся более подробно на отдельных методах. При 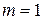получаем схему Эйлера. При 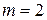получаем семейство методов

, ,

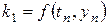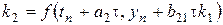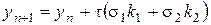. (8.14)

Исследуем погрешность аппроксимации методов (8.14) в зависимости от выбора параметров. Исключая из последнего уравнения функци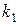и и 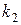, получаем

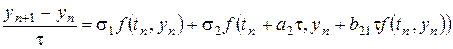. (8.15)

По определению погрешностью аппроксимации или невязкой метода (8.14) называется выражение

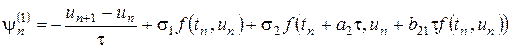, (8.16)

полученное заменой в (8.15) приближенного решения 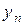точным решением .

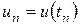Найдем порядок погрешности аппроксимации в предположении достаточной гладкости решения 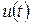и функции 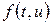. Для этого разложим все величины, входящие в выражение (8.16), по формуле Тейлора в точке 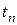. Имеем

,

,

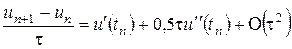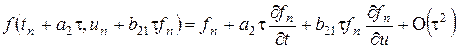где 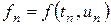. Далее, согласно (8.12), получим

.

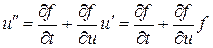Поэтому (доказать)

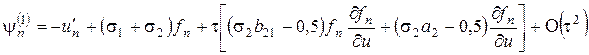. (8.17)

Отсюда видно, что методы (8.14) имеют первый порядок аппроксимации, если 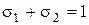. Если же дополнительно потребовать 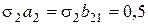, то получим методы второго порядка аппроксимации. Таким образом, имеется однопараметрическое семейство двухэтапных методов Рунге-Кутта второго порядка аппроксимации. Из формулы (8.17) видно, что наивысший достижимый порядок аппроксимации равен двум. Двухэтапных методов третьего порядка аппроксимации не существует. Это семейство методов можно записать в виде

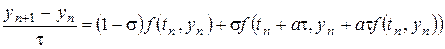, (8.18)

где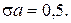

В частности, при 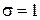, 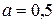получаем метод, рассмотренный в примере 3 предыдущего параграфа. При 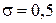, 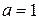получаем другой метод второго порядка:

, ,

.

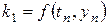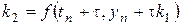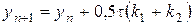Построить двухэтапный метод для уравнения 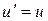. В данном случае двухэтапный метод Рунге-Кутта (8.18) принимает вид

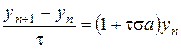
и погрешность аппроксимации равна

.

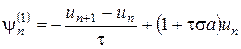Разлагая 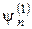по формуле Тейлора и учитывая, что 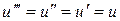, получим

, .

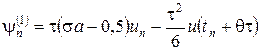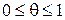При 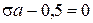получаем семейство двухэтапных методов второго порядка.

Рассмотрим метод третьего порядка аппроксимации (дом. зад. №1, найти порядок аппроксимации):

, ,

,

.

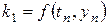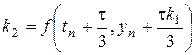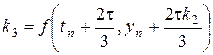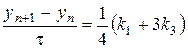Метод четвертого порядка аппроксимации (дом. зад. №1, найти порядок аппроксимации):

, ,

, ,

.

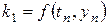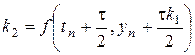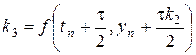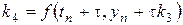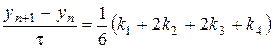Еще один метод четвертого порядка аппроксимации (дом. зад. №1, найти порядок аппроксимации):

, ,

, ,

.

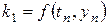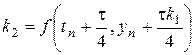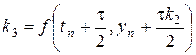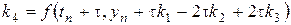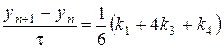Можно доказать, что методы Рунге-Кутта сходятся и порядок их точности совпадает с порядком аппроксимации.

Выпишем уравнение, которому удовлетворяет погрешность 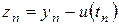. Основное уравнение метода Рунге-Кутта имеет вид

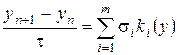, (8.19)

где

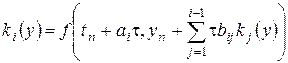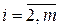, , (8.20)

.

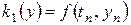Подставим в левую часть уравнения (8.19) вместо 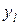выражения 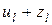при 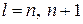, а в правой части этого уравнения добавим и вычтем сумму

,

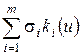где

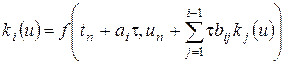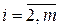, , (8.21)

.

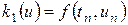Тогда уравнение (8.19) примет вид

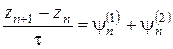, (8.22)

где

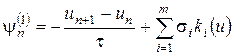(8.23)

есть по определению погрешность аппроксимации метода (8.19), (8.20) на решении исходной задачи (8.12) (невязка) и

.

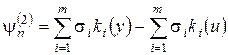Теорема 1. Пусть правая часть уравнения (8.12) 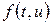удовлетворяет условию Липшица по второму аргументу с константой 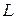. Пусть 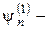невязка метода Рунге-Кутта (8.19), (8.20), определенная согласно (8.23). Тогда для погрешности метода при 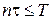справедлива оценка

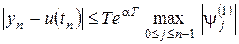, (8.24)

где

,

, .

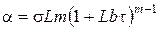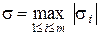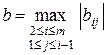Дата добавления: 2014-01-13