Специальные определения устойчивости

При исследовании разностных методов для жестких систем уравнений обычно рассматривают уравнение

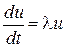, (8.78)

где 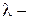произвольное комплексное число. Свойства различных разностных методов изучают и сопоставляют на примере модельного уравнения (8.78). Для того чтобы уравнение (8.78) действительно моделировало исходную систему

,

необходимо рассматривать его для всех таких , которые являются собственными числами матрицы .

Разностный метод (8.64)

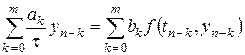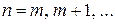, , (8.64)

примененный к уравнению (8.78), имеет вид (доказать)

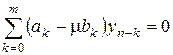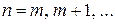, , (8.79)

где комплексный параметр.

Если искать решение уравнения (8.79), имеющие вид 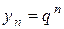, то для 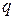получим характеристическое уравнение

, (8.80)

отличающееся от уравнения (8.65)

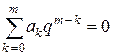(8.65)

тем, что его коэффициенты зависят от параметра 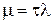. При малых 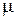корни уравнения (8.65) и (8.79) близки. Однако в дальнейшем мы не будем делать предположений относительно малости .

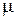Кроме обычного определения устойчивости разностного метода (все корни характеристического уравнения (8.79) не превосходят по модулю единицу 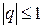), в случае жестких систем используют и другие, более узкие определения устойчивости. В данном случае рассмотрим 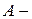устойчивый метод.

Введем следующее понятие. Областью устойчивости разностного метода (8.64)

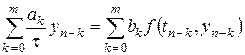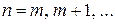, . (8.64)

называется множество точек комплексной плоскости 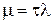, для которых данный метод, примененный к уравнению (8.78)

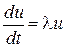, (8.78)

является устойчивым.

Рассмотрим, например, явный метод Эйлера

.

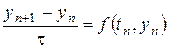В применении к уравнению (8.78) этот метод принимает вид (доказать)

, .

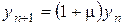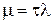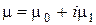Условие устойчивости для комплексного означает, что 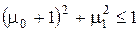. Тем самым область устойчивости данного метода представляет собой круг единичного радиуса с центром в точке 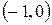. Для неявного метода Эйлера

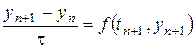
областью устойчивости является внешность круга единичного радиуса с центром в точке 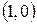(доказать).

Разностный метод называется 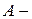устойчивым, если область его устойчивости содержит левую полуплоскость 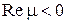. Отметим, что уравнение (8.78) асимптотически устойчиво при 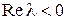. Поэтому сущность приведенного определения состоит в том, что 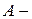устойчивый разностный метод является абсолютно устойчивым (устойчивым при любом 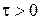), если устойчиво решение исходного дифференциального уравнения.

Нетрудно видеть, что неявный разностный метод Эйлера является 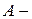устойчивым, а явный метод Эйлера – не является.

Рассмотрим одношаговый метод второго порядка точности

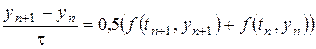. (8.81)

Для уравнения (8.78) метод принимает вид (доказать)

, откуда .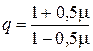

Отсюда видно, что 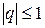тогда и только тогда, когда 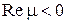(доказать). Следовательно, метод (8.81) является 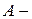устойчивым.

При решении жестких систем уравнений желательно пользоваться именно 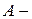устойчивыми разностными методами, так как условия их устойчивости не накладывают ограничений на шаг 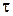. Оказывается, однако, что класс 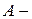устойчивых методов весьма узок. В частности, среди методов вида (8.79) не существует явных 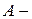устойчивых методов.

Для доказательства запишем характеристическое уравнение (8.80)

, (8.80)

в виде

. (8.82)

Если (8.79) ‑ явный 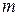-шаговый метод, то 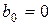, 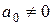. Могут оказаться равными нулю и другие коэффициенты 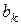, но не все, так как по условию 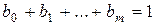. Пусть , , 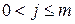. Тогда из (8.82) получим

.

Отсюда видно, что при больших 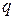функция 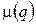ведет себя как , .

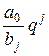Следовательно, для любого достаточно большого по модулю числа 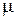, в том числе, и для 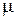, лежащих в левой полуплоскости, найдется корень 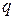уравнения (8.80) с .

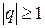Можно доказать, что среди неявных линейных многошаговых методов нет 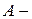устойчивых методов, имеющих порядок точности выше второго. Примером 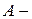устойчивости метода второго порядка точности является симметричная схема (8.81).

Дата добавления: 2014-01-13