Тема 4. Математические основы теории автоматического управления

Биодеградация пестицидов.

Биодеградация нефтяных загрязнений.

Технология переработки отходов молочной промышленности.

Ключевые слова и понятия

биодеградация гидролизаты детергенты красители

ксенобиотики органические пигменты пестициды сбраживание

Вопросы для контроля знаний:

1. Категории промышленных отходов.

2. Проблемы переработки промышленных отходов.

4. Продукты, получаемые из молочной сыворотки.

5. Технология переработки отходов целлюлозно-бумажной промышленности.

6. Переработка отходов от производства красителей.

9. Биодеградация поверхностно-активных веществ.

Взаимозависимость динамических характеристик объекта управления вытекает непосредственно из моделей типовых возмущений. Если обозначить переходный процесс, как реакцию объекта на единичный скачок, за H(t ), а весовую функцию, как реакцию объекта управления, на прямоугольный импульс, за h(t), то эта взаимосвязь вытекает непосредственно из внешнего вида этих типовых возмущений: .

Основополагающей моделью, в теории автоматического управления, является интеграл Дюамеля, который связывает между собой входные, X(t) и выходные, Y(t) параметры, объекта управления: и применяется для прогноза будущего поведения объекта управления.

Большое значение в приложениях теории автоматического управления играет и нтеграл Винера: , где К_ХХ(t) – автокорреляционная функция управляющего воздействия, К_ХY(t) – взаимокорреляционная функция управляющего воздействия и критерия управления, h(t) – весовая динамическая характеристика объекта управления.

Интеграл показывает, что динамические свойства объекта управления, h(t), полностью определяются статистическими характеристиками входных и выходных параметров объекта.

К основным свойствам автокорреляционной функции относятся дисперсия измеренного управляющего сигнала, D_X², как значение автокорреляционной функции в нуле, Т, как интервал времени от точки перегиба до пересечения касательной с осью абсцисс (время). Важнейшим свойством автокорреляционной функции является чётность. Это свойство и позволяет по экспериментальной (прошлой) информации прогнозировать текущие значения будущего состояния объекта управления.

К основным свойствам взаимокорреляционной функции относится свойство нечётности, что позволяет прогнозировать время чистого запаздывания объекта управления, tзап, как длину участка времени от нуля до времени выхода максимального коэффициента корреляции между входным и выходным параметром объекта управления.

Не менее важным, в приложениях теории автоматического управления, является интеграл Винера – Хинчина. Он связывает между собой автокорреляционные функции управляющего воздействия и критерия управления. Действительно, по определению автокорреляционная функция критерия управления это: 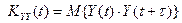. Если учесть интеграл Дюамеля, согласно которому: , то математическое ожидание произведения двух случайных функций, смещенных на время τ, будет иметь вид: . Это интегральное уравнение имеет большое применение как в задачах системного анализа, так и в задачах синтеза алгоритмов оптимального управления.

В современных условиях, когда для управления техническими системами широко применяется вычислительная техника, большое значение имеет матричное представление уравнения Винера, которое называют уравнением Винера- Хопфа:

.

Решением этого матричного уравнения, относительно динамических свойств объекта управления, будет массив весовых коэффициентов динамической характеристики объекта управления:

,

где - вектор строка, представляющая собой массив весовых коэффициентов объекта управления, - вектор столбец, представляющая собой массив элементов взаимокорреляционной функции, - обратная матрица из элементов автокорреляционной функции управляющего параметра.

Качество переходных процессов оценивается по критериям, которые разделяются на параметрические и интегральные.

Параметрические критерии качества применяются для количественной оценки качества переходного процесса систем автоматического регулирования, как частного случая управления.

		Yзад(t)

α

Слайд 11. Параметрические критерии качества

На слайде 11 представлены основные параметрические критерии, наиболее распространённые в проектных расчетах и работах, связанных с эксплуатацией систем автоматического регулирования.

Одним из основных критериев качества является статическая погрешность процесса регулирования, ∆, как величина отклонения текущего значения критерия управления, Y(t), от величины задания, Y_зад(t), в момент времени окончания переходного процесса или время регулирования, T_Р. Для систем оптимального управления время регулирования отождествляют с периодом управления, T_У , то есть с интервалом времени, через который изменяют величину управляющего воздействия. Скорость переходного процесса, α, как величина обратная времени пересечения касательной, проведенной к началу координат, до пересечения с заданием, Y_зад(t). Этот критерий имеет большое значение для задач анализа свойств управляющих воздействий и синтеза алгоритмов управления с максимальным быстродействием.

Степень колебательности переходного процесса: , где Y₁ - величина первого перерегулирования, Y₂ - величина второго перерегулирования. Под перерегулированием понимают величину превышения текущего значения переходного процесса над величиной задания, Y_зад(t).

По величине первого перерегулирования, Y₁, судят о динамических погрешностях в системах управления, так как они самые большие и могут привести к потере устойчивости всей технической системы.

Дата добавления: 2014-01-14