Слайд 37. Соединение при компенсации возмущений

Рассмотрим случай, когда возмущение приложено к входу регулятора (см. слайд 38). Такие соединения применяют для компенсации возмущений, приходящих со стороны регулятора. Эти возмущения можно создавать программным путем, а поэтому их можно измерять, прогнозировать, а, главное изменять (корректировка настроек регулятора). В этом случае:

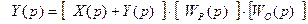
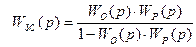
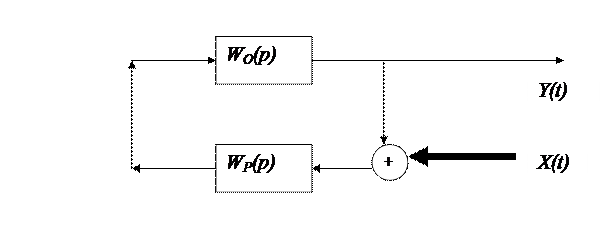
Слайд 38. Соединение при компенсации отклонений от задания

Анализ обоих типов соединений и их передаточных функций, W_ЗС(p), позволяет увидеть, что основные свойства замкнутой системы управления зависят только от частотных свойств разомкнутой системы:

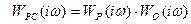
Еслиэти четыре правиладополнить правилами структурных преобразований блок-схем, то образуется достаточно эффективный способ структурного синтеза, как моделей объекта управления, так и моделей управляющих устройств.

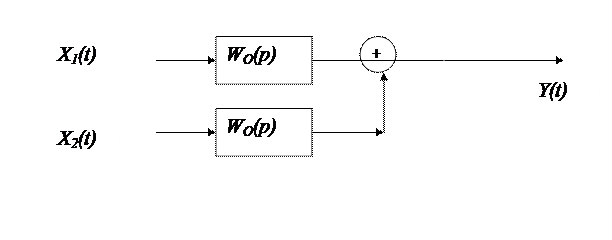
Правило 1. Перенос сумматора через звено по ходу сигнала. Частотные свойства выходного сигнала, Y(t), не изменятся, при переносе сумматора через звено, если в схему добавить такое же звено.

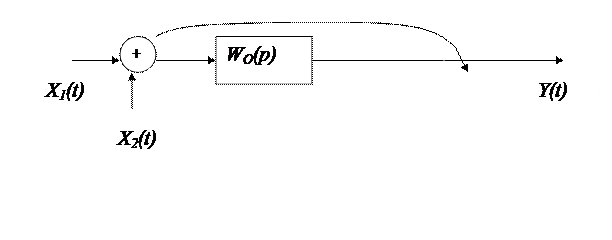
Действительно, согласно исходной схеме: 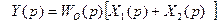и если реализовать правило, то соотношение примет вид: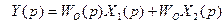, что одно и тоже.

Правило 2. Перенос звена через сумматор по ходу сигнала. Частотные свойства выходного сигнала, Y(t), не изменятся, при переносе звена через сумматор, если в схему добавить инверсное звено.

Действительно, согласно исходной схеме: 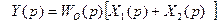и если реализовать правило 2, то соотношение примет вид: .

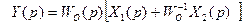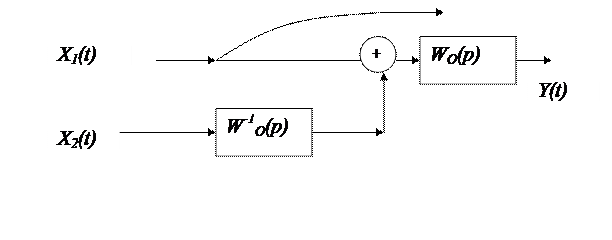
Правило 3. Перенос узла по ходу сигнала. Частотные свойства выходного сигнала, Y(t), не изменятся, при переносе узла через звено, если в схему добавить инверсное звено.

Действительно, согласно исходной схеме:

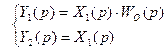
и если реализовать правило 3, то соотношение примет вид:

.

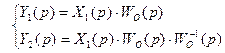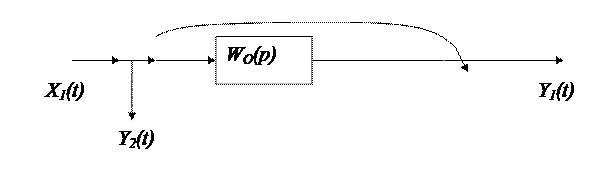
Правило 4. Перенос узла против хода сигнала. Частотные свойства выходного сигнала, Y(t), не изменятся, при переносе узла через звено против хода сигнала, если в схему добавить аналогичное звено.

Действительно, согласно исходной схеме:

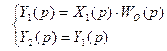
и если реализовать правило 4, то соотношение примет вид:

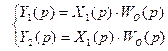
Пример. Найти частотную модель объекта управления, W₀(p), который задан структурной схемой (см. слайд 39). Решение осуществляется методом последовательных приближений путём последовательного применения правил преобразований.

На первом шаге исключаются все последовательные соединения путём введения обозначений (см. слайд 40)

.

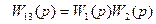
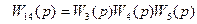
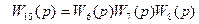
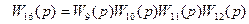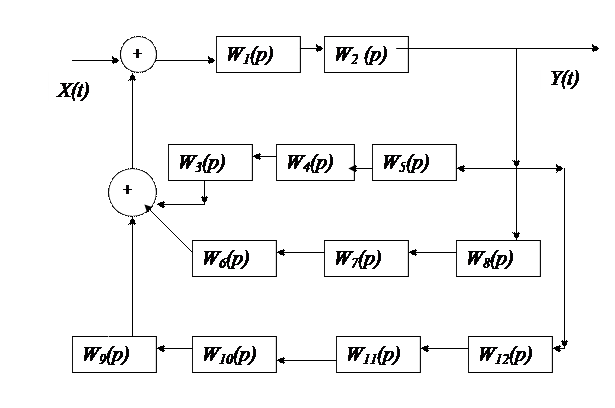
Слайд 39. Исходная схема

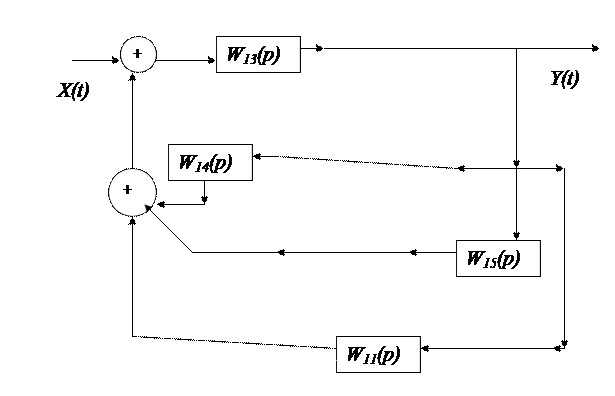
Слайд 40. Схема после первого шага преобразований

На втором шаге исключаются все параллельные соединения

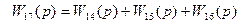
Слайд 41. Схема после второго шага преобразований

Шаг 3. Исключаются все встречно-параллельные соединения

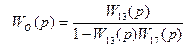
Шаг 4. Принятие решения об окончании: если упрощений нет, то идти на шаг 5, а если упрощения есть идти на шаг 1.

Шаг 5. Получаем модель объекта управления обратной подстановкой обозначений

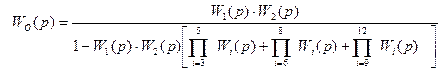
Тема 6. Устойчивость динамических систем

Теория академика А.М. Ляпунова, созданная в конце XIX века, в настоящее время существенно развита в основном отечественными учёными. Основу теории составляют теоремы в форме необходимых и достаточных условий устойчивости возмущённой динамической системы.

Ключевым понятием теории устойчивости является понятие асимптотической устойчивости. Рассмотрим физический смысл этого понятия на примере модели движения самолета с постоянной скоростью.

Пусть модель дана в виде системы дифференциальных уравнений:

,

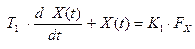
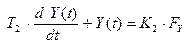
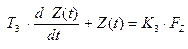
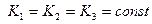
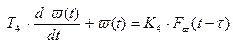где X(t), Y(t), Z(t) – пространственные координаты движения самолёта в реальном масштабе времени.

Пусть известно решение системы F (X,Y,Z,t). Это решение будем называть программным (эталонным). (У Ляпунова – невозмущенное движение). Любое отличие от эталонного движения будем называть возмущённым движением (см. слайд 42).

F (X,Y,Z,t)

Слайд 42 К понятию асимптотической устойчивости

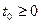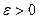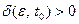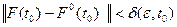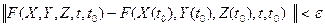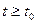Первое начало Ляпунова. Невозмущенное движение F⁰(t) называется устойчивым по Ляпунову, если для любого и любого числа можно указать число , такое, что при норме разности будет при , где 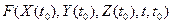-это возмущенное движение, проходящее через точку 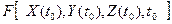в момент .

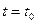Здесь под нормой понимается 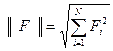. По Ляпунову этот объект устойчив в «большом» и является асимптотически устойчивым (см. слайд 9).

Робастная устойчивость или второе начало Ляпунова. Допустим, что K₁ (t), K₂ (t), K₃ (t) – это случайный процесс (дрейф коэффициентов модели):

,

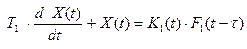
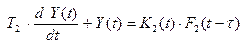
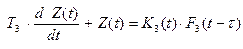
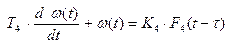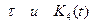- это случайное число и случайная функция.

Тогда, не возмущенное движение F⁰(t) называется асимптотически устойчивым по Ляпунову если:

1) оно устойчиво по Ляпунову;

2) величину 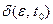для любого 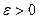можно выбрать так, что норма разности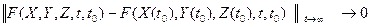

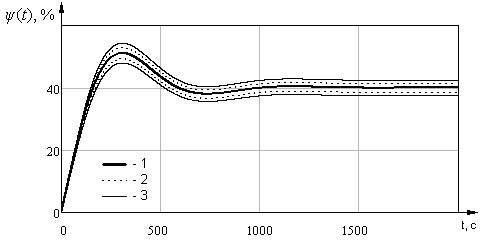
Слайд 43. К понятию робастной устойчивости

Такие системы называются устойчивыми в «малом» (см. слайд 9)

Дата добавления: 2014-01-14