Учебные цели. Источники и классификация погрешностей результата численного решения задачи

Источники и классификация погрешностей результата численного решения задачи.

Точность вычислительного эксперимента.

Для правильного решения прикладных задач на ЭВМ очень важно признать, что получить точное значение интересующей величины практически не возможно и не в этом цель вычислений. Получаемое на ЭВМ решение y почти всегда (за редким исключением) содержит погрешность, т.е. является приближенным.

Основные источники погрешности математического моделирования:

а) математическая модель является лишь приближенным, описанием реального процесса. Характеристики процесса, вычисленные в рамках приятной модели, заведомо отличаются от истинных характеристик, причем их погрешность зависит от степени адекватности модели реальному процессу.

б) исходные данные, как правило, содержит погрешности, поскольку они либо получаются в результате экспериментов (измерений), либо являются результатом решения некоторых вспомогательных задач.

в) применяемые для решения задачи методы в большинстве случаев являются приближенными. Найти решение возникающей на практике задачи в виде конечной формулы возможно лишь в отдельных очень упрощенных ситуациях, да и то часто вычисление интеграла заменяют вычислением суммы, значения функции интерполируются табличными данными.

г) при вводе исходных данных в ЭВМ, выполнении арифметических операций и выводе результатов на печать, экран производит округления.

Пусть y - точное значение величины, вычисление которой является целью поставленной задачи, y^* - получаемое на ЭВМ решение. Различие между величинами y и y^* определяет величину погрешности dy.

Погрешность d_нy - соответствующая первым двум причинам называется неустранимой погрешностью. Такое название вызвано тем, что математическая модель и исходные данные вносят в решение ошибку, которую нельзя устранить в процессе дальнейшего решения.

Погрешность d_мy источником которой является метод решения называется погрешностью метода, а погрешностью d_вy - возникающую при вводе, вычислениях и выводе называют вычислительной погрешностью.

Полная погрешность результата решения задачи на ЭВМ dy=y-y^* складывается из этих трех погрешностей: dy=d_нy+d_мy+d_вy; желательно, чтобы и .

§2 Приближенные числа. Абсолютная и относительная погрешности.

а) приближенные числа. ЭВМ обрабатывает числа, которыезаписаны в форматах с фиксированной запятой и плавающей запятой.

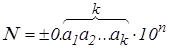Рассмотрим десятичные действительные числа с фиксированной запятой: 5.1; -10.2; 175.12; 0.0093 и т.п. Эти же числа можно представить в виде: ;-; , т.е., в общем случае, , где к - разрядность мантиссы числа, n - порядком числа.

Из этой записи следует, что действительные числа, с которыми оперирует ЭВМ не являются бесконечными, т.к. разрядность к и границы порядка n конечны. Обычно к = 7, а .

Таким образом, число будет представлено в ЭВМ в виде , т.е. приближенно и отличаться от истинного значения на величину .

Процесс представления числа с меньшим количеством разрядов называется округлением. Существует несколько способов округления. Наиболее простой из них - усечение состоит в отбрасывании меньших разрядов. Чаще используется округление по дополнению, в котором, если первая слева отбрасываемая меньше 5, то сохраняется значение младшего сохраняемого разряда, если же отбрасываемая цифра , то к младшему сохраняемому разряду добавляют единицу. Следовательно, ЭВМ оперирует с приближенными значениями действительных чисел. Мерой точности приближенных чисел является погрешность.

Максимальная относительная погрешность ЭВМ, связанная с округлениями при вводе, выводе и выполнении арифметических операций называется машинным эпсилон и обозначается e_m, она характеризует точность ЭВМ.

б)абсолютная и относительная погрешность. Пусть a - точное (вообще говоря, неизвестное число) является значением некоторой величины; а^* - известное приближенное значение той же величины (приближенное значение). Ошибкой (или погрешностью) приближенного числа а называют разность a-a^* между точным и приближенным значением.

Простейшей количественной мерой ошибки является абсолютная погрешность:

, (2.1)

где 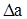>0 -положительная величина. Это равенство можно разделить на два:

.

Рассмотрим равенство со знаком “+”: . Возьмем модуль: 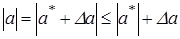(по правилу треугольников).Отсюда

, . (2.2)

Рассмотрим равенство со знаком “-“: 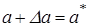. Возьмем модуль: . Имеем: или

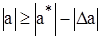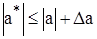, . (2.3)

По величине абсолютной погрешности не всегда можно сделать правильное заключение о качестве приближения. Пусть 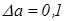. Много это или мало? Ответ зависит от величины а. Если а= 0,2, то погрешность велика, если а=10⁶, то погрешность мала. Естественно соотнести погрешность величины и ее значение. Для этого вводится относительная погрешность величины а.

. (2.4)

Максимальное значение абсолютной погрешности называется предельной абсолютной погрешностью и обозначается .

Максимальное значение относительной погрешности называется предельной относительной погрешностью и обозначается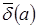

На основании этих определений можно записать:

Погрешность приближенного числа связана с количеством его верных знаков.

На практике количество верных знаков числа обычно отсчитывается от первой значащей цифры числа до первой значащей цифры его абсолютной погрешности: например, число S=20,7426 с абсолютной погрешностью 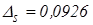имеет три верных знака (2,0,7); остальные знаки - сомнительные. Также считают, что количество верных знаков числа равно порядку относительной погрешности, взятому с противоположным знаком, т.е. наличие одного верного знака соответствует относительной погрешности порядка 10%, двух верных знаков - погрешности порядка 1%, трех верных знаков - погрешности порядка 0,1% и т.д.

В математических таблицах все числа округлены до верных, при этом абсолютная погрешность чисел не превосходит половины единицы последнего оставленного разряда. Например, если в таблице указано е=2,718, то абсолютная погрешность не превосходит .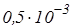

В окончательных результатах вычислений обычно оставляют, кроме верных знаков, один сомнительный знак.

В промежуточных результатах вычислений обычно сохраняют два-три сомнительных знака, чтобы не накапливать лишних погрешностей от округлений.

в) погрешности арифметических операций. Правила оценки погрешностей.

а) При сложении и вычитании чисел их абсолютные предельные погрешности складываются;

б) При умножении и делении чисел друг на друга их относительные предельные погрешности складываются;

в) При возведении в степень приближенного числа его относительная предельная погрешность умножается на показатель степени.

отсюда

(2.5)

т.к. и , то: , следовательно:

(2.6)

т.к. . Отсюда:

. (2.7)

,

(2.8)

В дальнейшем под погрешностью мы будем понимать предельную погрешность (эту величину можно измерить, рассчитать, оценить), поэтому значок - вверху у предельных погрешностей ставить не будем.

г) погрешности функций. Рассмотрим функцию одной переменной y=f(x). Пусть а - значение аргумента x, 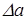- абсолютная погрешность, т.е. 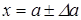. Можем записать

Абсолютную погрешность функции можно считать ее приращением, которое можно заменить дифференциалом: 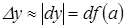. Тогда для оценки абсолютной погрешности имеем

(2.9)

Относительная погрешность функции определяется как:

(2.10)

Выражения (2.9, 210) распространяются на любые функции одной переменной, в частности соотношения (2.5, 2.8) являются частными случаями формул (2.9, 2.10).

Аналогичные выражения можно записать для функции нескольких переменных: x»a, y»b, z»c;

(2.11)

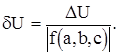(2.12)

д) погрешность малой разности больших чисел.

Рассмотрим два больших числа и ,имеющих одинаковый знак, когда разность между ними много меньше любого из них, т.е. .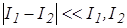

Пусть 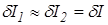. Вычислим относительную погрешность разности :

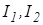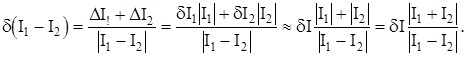(2.13)

т.к. 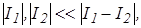то относительная погрешность малой разности двух больших чисел больше относительной погрешности каждого из этих чисел на величину, равную отношению суммы этих чисел на их разность.

Вывод: При вычислении малой разности больших чисел на ЭВМ из-за ошибок округления погрешность вычисления резко возрастает, и это может привести к неверному результату.

1. Пять, что изучает экономическая теория.

2. Изучить методы экономического анализа.

3. Выяснить различия между нормативной и позитивной экономикой.

4. Уяснить, чем отличается микроэкономика от макроэкономики и почему они связаны друг с другом.

5. Раскрыть содержание таких понятий, как принципы, законы, модели.

6. Вывить характер возможных связей и зависимостей между различными макроэкономическими целями развития.

7. Обратить внимание на логические ошибки, возможные в научном анализе при обращении фактов и познании явлений.

Дата добавления: 2014-01-14