Дисконтирование

Дисконтирование и учет по простым ставкам.

Определение. Дисконтирование это процесс заключающийся в определение стоимостной величины A на некоторый момент времени, если известно, что в будущем она имеет заданную величину S.

Из этого определения следует, что задача дисконтирования является обратной задачи определения наращенной суммы. Расчет величины A называют приведением суммы S к заданной дате, а саму сумму A, найденную дисконтированием, называют современной или приведенной величиной S.

Определение. Проценты, полученные в результате дисконтирования: D=S-A, называются дисконтом, а сам процесс начисления и удержания этих процентов называется учетом.

Задача дисконтирования может возникнуть, например, при покупке векселей, оплата по которым будет произведена в будущем, или же, когда проценты при выдаче ссуды удерживаются непосредственно при выдаче ссуды и т.д.

В зависимости от вида применяемой ставки применяют два вида дисконтирования. - математическое дисконтирование и банковский (коммерческий) учет.

4.2 Математическое дисконтирование представляет собой решение задачи обратной наращению первоначальной суммы. Поэтому решив уравнение (1.2), в котором величина P замена на величину A, при заданном S получаем:

(1.5)

где n_i - дисконтный множитель. Дисконт соответственно будет равен:

(1.6)

Из (1.5) следует, что с увеличение срока n дисконтный множитель уменьшается.

4.3 Банковский учет (учет векселей). Операция банковского учета заключается в том, что банк или иное финансовое учреждение покупает вексель или другое платежное обязательство у его владельца до наступления срока платежа по цене, меньшей той суммы, которая должна быть выплачена по этому обязательству в конце срока. Банк при наступление срока получает прибыль, т.е. реализует дисконт, а владелец, с помощью учета, получает деньги ранее указанного в документе срока. При учете применяется банковский или коммерческий учет (bank discount). Согласно этому методу проценты начисляются на сумму, подлежащую уплате в конце срока ссуды. При этом применяется учетная ставка d.

Определение. Учетная ставка d равна отношению дисконта D _T, полученного за определенный фиксированный интервал времени T к величине суммы S, которую необходимо оплатить в конце срока ссуды: d=D _T/ S. Ставка измеряется в процентах, в виде десятичной или натуральной дроби.

При простой учетной ставке дисконт I_D за время t (от учета до конца срока ссуды), равное n периодам 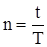, вычисляется по формуле:

(1.7)

Сумма A, которую необходимо выплатить при учете соответственно будет равна:

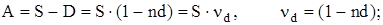(1.8)

где n_d - дисконтный множитель.

Дисконтирование по простой учетной ставке производится чаще всего при условии, что год равен 360 дней (T =360 дней), а число дней в периоде вычисляется точно. Заметим также, что n должно быть меньше, чем 1/d, в противном случае получим отрицательную современную величину будущей суммы S.

4.4 Наращение по простой учетной ставке. Простая учетная ставка может быть применена и при расчете наращенной суммы, например, при определении суммы P, которую необходимо указать в векселе, если известна сумма ссуды, которая будет получена при учете, срок погашения векселя и учетная ставка.

В соответствии с (1.8) заменяя A на P наращенная сумма будет равна:

(1.9)

При d=i из очевидного неравенства: следует, что простая учетная ставка d дает более быстрый рост суммы ссуды чем такая же простая процентная ставка i.

Операции начисления процентов и дисконтирования по учетной ставке могут совмещаться, при учете платежного обязательства, предусматривающего начисление простых процентов. В этом случае сумма долга на конец срока представляет собой наращенную сумму, а учет проводиться раньше этого срока. Следовательно можем записать:

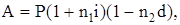
где P - первоначальная сумма ссуды, A - сумма полученная при учете обязательства, n₁ - общий срок платежного обязательства, n₂ - срок от учета до даты погашения (n₁>n₂).

4.5. Определение продолжительности ссуды и уровня процентной и учетной ставок. При разработке условий контрактов возникает необходимость в решении обратных задач - определение срока ссуды и уровней процентной и учетной ставок при всех прочих равных условиях. Из (1.2) и (1.8) легко получаем формулы для расчета продолжительности срока ссуды в годах:

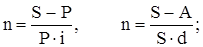(1.10)

и в днях:

(1.11)

а также формулы для определения процентной и учетной ставок:

(1.12)

Дата добавления: 2014-01-14