Статистические характеристики модели и эксперимента

Обычная последовательность реализации метода регрессионного анализа состоит в следующем:

1. Установление наличия зависимости между входами и выходами.

2. Выбор класса функций, которые могли бы описать связь между входами и выходами, если установлено, что она существует (например, полином (2.6)).

3. Выбор конкретной функции для обработки. Последовательность выбора: от простого в сторону усложнения. Пункт 1 фактически означает выбор простейшей зависимости 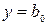. Если зависимость может быть линейной, то 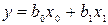для одного фактора, 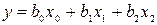- для двух и т.д., т.е. задается число факторов и, следовательно, число коэффициентов полинома.

4. Анализ числа степеней свободы. Первоначальное число степеней свободы модели определяется как разность между числом опытов и числом коэффициентов модели: f = n - m. Чем больше опытов, тем больше информации о модели, эта информация используется для того, чтобы определить ее коэффициенты. Отсюда ясно, что максимальное число коэффициентов модели, которое можно определить на основе проведенного эксперимента, равно числу опытов. Но в этом случае не остается степеней свободы для нахождения статистических характеристик, с помощью которых можно оценить адекватность модели и оригинала. Чем больше остается степеней свободы после расчета коэффициентов, тем более достоверными можно считать результаты статистической обработки. Каждой статистической оценке эксперимента соответствует определенное текущее число степеней свободы.

5. Проверка адекватности. Если модель неадекватна эксперименту, надо возвратиться к пункту 3, усложнить модель, проанализировать степени свободы, и снова проанализировать адекватность. Если теперь модель адекватна эксперименту, можно двигаться дальше.

6. Оценка значимости коэффициентов. Значимые коэффициенты остаются в модели, незначимые можно удалить, изменив тем самым модель. В случае удаления незначимых коэффициентов, снова проводится проверка адекватности. Если все коэффициенты значимы, оценивается погрешность в определении коэффициентов.

Дата добавления: 2014-01-14