Импульсной переходной (весовой) функцией звена w(t)называется реакция звена на единичную импульсную функцию, так называемую дельта-функцию

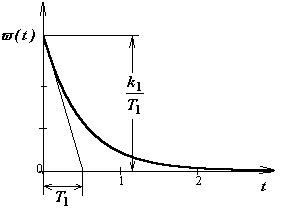
Импульсная переходная функция звена

(Весовая функция звена)

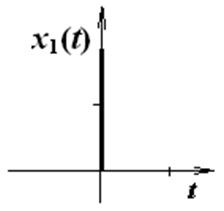
Дельта-функция представляет собой производную от единичной ступенчатой функции и равна нулю повсюду, кроме точки t =0, где она равна ¥.

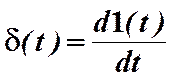
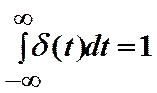
Связь между переходной функцией и импульсной переходной функцией:

Переходная фунция:

х ₁(t) = 1(t), то х ₂(t) = h (t),

Импульсная переходная функция:

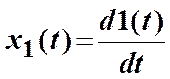, то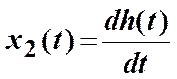

Отсюда следующее соотношение между весовой и переходной функциями звена

, .

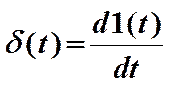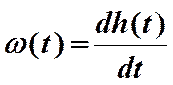Частотные характеристики звена

Частотными характеристиками звена называются формулы и графики, характеризующие реакцию звена на синусоидальное входное воздействие в установившемся режиме, т.е. вынужденные синусоидальные колебания звена.

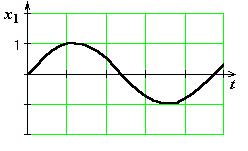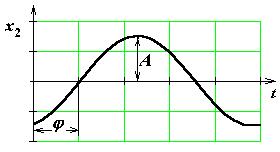Если на вход звена подается х ₁(t)= sinwt, тона выходе звена будет (в установившемся режиме) сигнал х ₂(t)= Asin (wt+j), где A – амплитуда (усиление амплитуды), j – фаза (сдвиг по фазе)

В ТАУ для нахождения выражения для частотной характеристики применяют комплексное синусоидальное входное воздействие вида

х ₁(t)= е^jwt, или х ₁(t)= cos (wt)+ j×sin (wt).

Пусть имеется уравнение

.

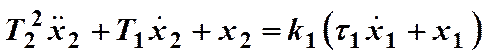Если х ₁(t)= е ^jwt,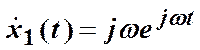,тогда

, , .

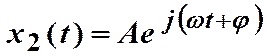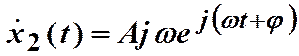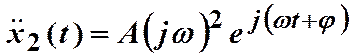Подставив эти величины в уравнение звена, получим

,

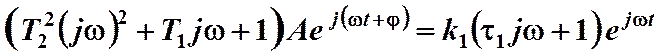откуда

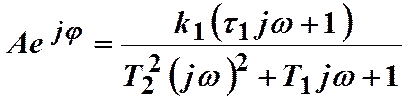
Сравнивая это выражение с передаточной функцией данного звена, видим, что

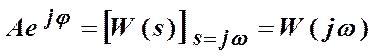
W (jw) – амплитудно-фазовая частотная характеристика звена (АФЧХ)

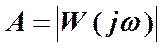– амплитудная частотная характеристика (АЧХ).

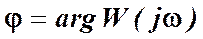– фазовая частотная характеристика (ФЧХ).

Графически амплитудно-фазовая частотная характеристика (АФЧХ) строится на комплексной плоскости в полярных координатах (A, j), как годограф функции W (jw). Можно

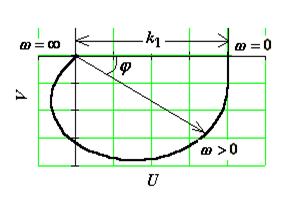строить АФЧХ и в прямоугольных координатах (U, V), выделив в выражении W (jw) вещественную и мнимую части:

Амплитудно-фазовая частотная характеристика (АФЧХ) – это геометрическое место концов векторов амплитуд на комплексной плоскости, которые соответствуют передаточной функции W (jw)= U (w)+j V (w) при изменении круговой частоты от нуля до бесконечности.

Амплитудная частотная характеристика (АЧХ) показывает изменение амплитуды выходно­го сигнала относительно амплитуды входного сигнала при изменении частоты от нуля до бесконечности.

Амплитудная частотная характеристика показывает, как пропускает звено сигнал различной частоты. Оценка пропускания делается по отношению выходной и входной величин.

Фазовая частотная характеристика (ФЧХ) показывает сдвиг фазы выходного сигнала относительно фазы входного сигнала при изменении частоты от нуля до бесконечности.

Фазовая частотная характеристика показывает фазовые сдвиги, вносимые звеном на различных частотах.

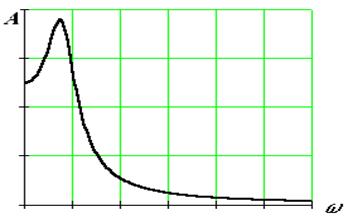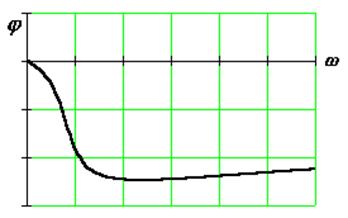АЧХ – четная функция, ФЧХ – нечетная функция.

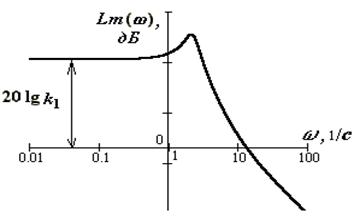
Логарифмические частотные характеристики

При построении логарифмической АЧХ по оси ординат откладывается величина:

,

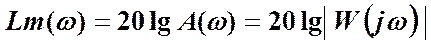которая измеряется в децибелах.

По оси абсцисс откладывается круговая частота в логарифмическом масштабе.

Начало координат обычно помещают в точку w = 1, т.к. lg 1 = 0 (точка w = 0 лежит в – ¥). Ось абсцисс (Lm =0) соответствует значению А =1. При этом верхняя полуплоскость ЛАХ соответствует значениям А > 1 (усиление амплитуды), нижняя полуплоскость – значениям А<1 (ослабление амплитуды).

Точка пересечения ЛАХ с осью абсцисс называется частотой среза. При этой частоте амплитуды входного и выходного сигналов равны.

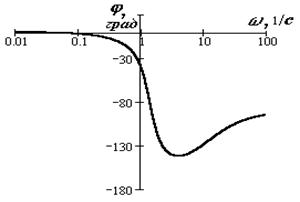При построении логарифмической ФЧХ отсчет углов по оси ординат идет в обычном масш­табе в угловых градусах. По оси абсцисс откладывается частота в логарифмическом масштабе

Дата добавления: 2014-01-14