Полиномы Чебышева

Лекция 3.

Разряд в длинных воздушных промежутках.

При развитии разряда в длинном (> 1 м) резконеоднородном разрядном промежутке при достижении напряжением начального значения со стержня развивается пучок стримеров. Образованный при этом объемный заряд приводит к уменьшению напряженности электрического поля вблизи электрода с малым радиусом кривизны, вследствие чего развитие разряда прекращается. Напряжение на промежутке возрастает, и через некоторое время становятся возможными новые вспышки стримеров. Вследствие нагрева воздуха в зоне развития стримеров появляется другое образование - канал лидера. Лидер имеет непосредственный контакт с электродом. Последующие вспышки стримеров возникают с конца лидера и приводят к его удлинению. Начиная с некоторого момента времени развитие разряда вместо вспышечного становится непрерывным.

При достижении стримерами плоскости начинается “сквозная фаза” развития разряда. В этой фазе резко возрастает ток разряда и вследствие возрастающего падения напряжения на внутреннем сопротивлении источника начинает уменьшаться напряжение на промежутке. Значение разрядного напряжения промежутка соответствует началу сквозной фазы. Сквозная фаза завершается перекрытием промежутка лидерным каналом и главным разрядом.

ГЛАВА 2. Приближение функций многочленами.

В пространстве многочленов введем скалярное произведение

.

Определение. Два многочлена называются ортогональными на промежутке [a, b] с весом , если

(1.1)

Многочлены, ортогональные на промежутке [-1, 1] с весом 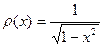, называются многочленами Чебышева. Они обозначаются .

Эти многочлены можно определить следующим образом:

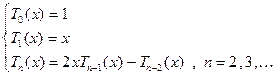(1.2)

Очевидно, для п > 0 будет .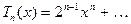

Возьмем промежуток и рассмотрим функции 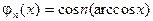. Это будут многочлены. Действительно, . Положим . Нетрудно проверить соотношение 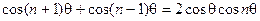. Отсюда получаем 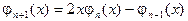. Значит,

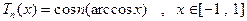
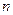Многочлен имеет на промежутке различных вещественных корней, которые имеют вид

-1 (1.3)

Найдем точки экстремума на . Это будут точки

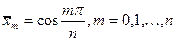(1.4)

Причем

Рассмотрим многочлен Это многочлен степени п со старшим коэффициентом 1. Можно положить 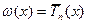. При этом будет .

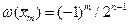Теорема. Пусть — произвольный многочлен степени п со старшим коэффициентом 1,не совпадающий с 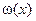. Тогда

Д о к а з а т е л ь с т в о. Пусть существует многочлен степени п со старшим коэффициентом 1, такой, что 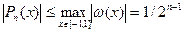при всех . Рассмотрим многочлен . Это многочлен степени п- 1. В то же время 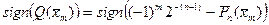. Но по условию , значит, знак скобки определяется первым слагаемым. Таким образом, получается . Значит, между любыми соседними точкам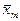и и этот многочлен меняет знак. Таких точек п +1. Значит, многочлен степени п- 1 имеет п различных корней.!!! g

Многочлен 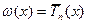называется многочленом, наименее уклоняющимся от 0 на промежутке .

§ 2. Разностные отношения (разделенные разности)

Пусть на промежутке [ a,b ] даны +1 точка 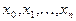и в этих точках даны значения некоторой функции : 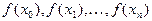. Предположим, что точки 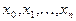различны и расположены на промежутке произвольным образом. Определение:

Разностными отношениями 1-го порядка функции в точках называются выражения

(2.1)

Такие выражения можно написать для любой пары точек.

Разностными отношениями 2-го порядка функции в точках 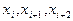называются выражения

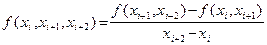(2.2)

Продолжая этот процесс, получим общую рекуррентную формулу, а именно:

Разностными отношениями k-го порядка функции в точках называются выражения

(2.3)

Разностные отношения обычно записываются в виде таблицы:

					...
				...	...
			...	...
		...	...
...	...	...

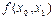
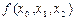
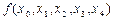
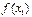
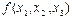
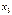
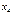
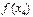
Рассмотрим пример.

xi	f(xi)	f(xi ,xi+1)	f(xi ,xi+1, xi+2)	f(xi,xi+1,xi+2,xi+3)
-2	-27
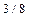
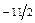
		-7	-2
	-6	-13	-3
	-32	-7
-1	-4

Это таблица разностных отношений для многочлена 3-й степени:

.

Дата добавления: 2014-01-14