Cвойства разностных отношений

1. Разностное отношение любого порядка суммы двух функций равно сумме разностных отношений слагаемых, т.е. если 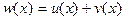, то

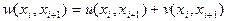
и т.д.

2. Разностное отношение любого порядка произведения функции на число равно произведению этого числа на разностное отношение функции, т.е. если 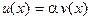, где a — вещественное число, то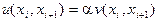

3. Разностное отношение первого порядка от полинома степени n есть полином

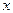степени n -1. Действительно, пусть . Возьмем 2 точки и 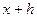. Тогда

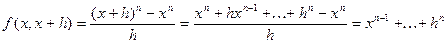. Это

многочлен степени n -1. Воспользовавшись свойствами 1) и 2), получаем наше

утверждение для любого многочлена. Из этого свойства получается утверждение,

что разностное отношение порядка п для любого многочлена степени п есть

постоянная, а разностное отношение порядка выше п для любого многочлена

степени п равно 0.

4. Для разностного отношения порядка k имеет место соотношение:

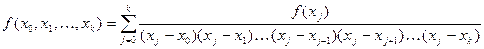(2.4)

Докажем это соотношение методом математической индукции.

Легко проверить, что соотношение (2.4) выполняется при k = 1. Предположим, что

это соотношение выполняется для любого разностного отношения порядка k -1.

Покажем, что оно выполняется для разностного отношения порядка k.

.

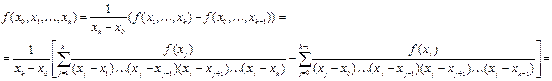
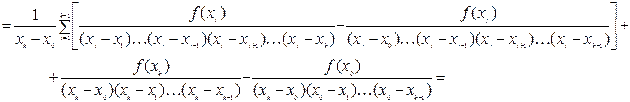
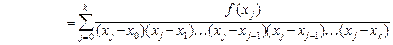5. В любой точке x_k функцию f можно представить в виде линейной комбинации разностных отношений до порядка к:

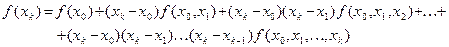(2.5)

Докажем это соотношение тоже методом математической индукции. Для k= 0

соотношение очевидно. Пусть оно выполняется для любого набора из k точек. Но

,следовательно

(2.6)

Запишем формулу (2.5) для точек x ₁ , x ₂ ... x _k:

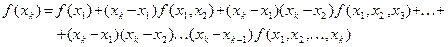
В эту формулу подставим выражения (2.6) при j = 1, 2,..., k.

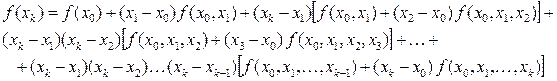
Приведя подобные члены, получим формулу (2.5).

Рассмотрим многочлен

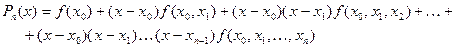(2.7)

Это многочлен степени n и при всех х ₀, х ₁ ,..., х_n имеет место:

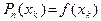
6. Связь разностных отношений с производными.

Теорема. Пусть на промежутке [a,b] даны n+1 точка x₀ , x₁,..., x_n и пусть заданная в этих точках функция имеет на промежутке [a,b] непрерывную n- ю производную. Тогда на промежутке [a,b] существует точка , такая, что

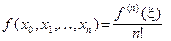(2.8)

Д о к а з а т е л ь с т в о. Пусть P_n (x) —многочлен (2.7). Рассмотрим вспомогательную функцию:

.

Эта функция n раз непрерывно дифференцируема на [ a,b ] и обращается в 0 в точках

x₀ , x₁,..., x_n, т.е. она имеет на промежутке [ a,b ] по крайней мере n +1 корень. По теореме Ролля функция на промежутке [ a,b ] имеет по крайней мере n корней. Применим теорему Ролля к функциии получим, что имеет на промежутке [ a,b ] по крайней мере n -1 корень. Продолжая, получим, что функция имеет на промежутке [ a,b ] по крайней мере 1 корень. Обозначим его . Получаем:

.

Дата добавления: 2014-01-14