Алгебраические интерполяционные многочлены

Пусть F — пространство вещественных на [ a, b ] функций. Пусть в n +1 попарно-различных на [ a, b ] точках 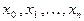даны значения некоторой функции 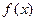из этого пространства. Построим алгебраический многочлен степени не выше n:

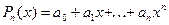, (4.1)

удовлетворяющий условиям

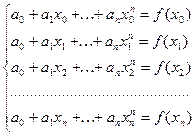(4.2)

Соотношения (4.2) образуют линейную алгебраическую систему относительно неизвестных коэффициентов многочлена (4.1). Определитель этой системы есть определитель Вандермонда, следовательно, отличен от 0, т.к. все значения 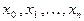попарно различны. Значит,многочлен (4.1), удовлетворяющий условиям (4.2) существует и единственен.

Определение. Алгебраический многочлен степени не выше n, совпадающий в п+1 точке 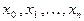со значениями в этих точках некоторой функции 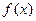, называется алгебраическим интерполяционным многочленом для функции 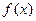, построенным по точкам 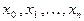. Точки 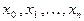называются узлами интерполирования. Интерполяционный многочлен можно использовать не только в канонической форме, т.е. в виде (4.1). Удобно применять и другие формы. Рассмотрим интерполяционный многочлен в форме Лагранжа.

Введем в рассмотрение многочлены 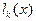степени n, удовлетворяющие условиям:

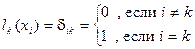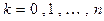, (4.3)

Эти многочлены имеют корнями при каждом k точки 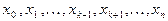, следовательно, они имеют вид:

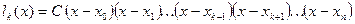, где С — некоторая константа. Найдем С из условия 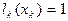, т.е.

.

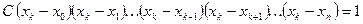Отсюда

.

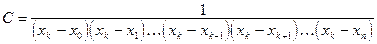Следовательно,

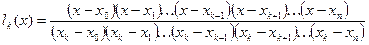(4.4)

Получим более компактную запись многочлена 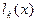. Введем в рассмотрение многочлен со старшим коэффициентом 1, имеющий корнями все точки 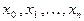. Обозначим его 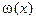, т.е.

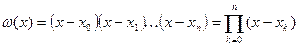(4.5)

Тогда

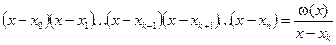(4.6)

Перейдем в этом равенстве к пределу при 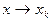, учитывая, что

.

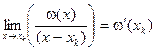Отсюда получаем

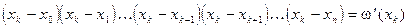(4.7)

Заменим числитель и знаменатель дроби (4.4) правыми частями равенств (4.6) и (4.7):

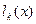
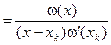. (4.8)

Многочлен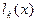называется многочленом влияния k - го узла. Всего таких многочленов п +1. Эти многочлены называют также фундаментальными многочленами интерполирования, а также интерполяционными множителями Лагранжа, или лагранжевыми коэффициентами.

Теперь рассмотрим многочлен

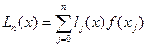(4.9)

Очевидно, это многочлен степени не выше п, т.к. он является суммой многочленов степени не выше п. В силу соотношения (4.3) выполнены условия

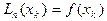(4.10)

Значит, это интерполяционный многочлен, построенный по точкам 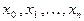. Многочлен 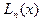называется интерполяционным многочленом в форме Лагранжа.

Пример построения многочлена в форме Лагранжа.

x	f(x)
0,8000	1,0320
0,9000	1,0090
0,6000	1,0960
Найти f(0,75)

Нужно построить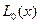

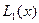
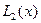
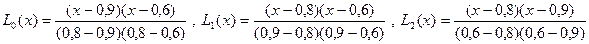
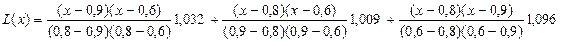
Подставляем .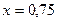

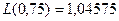
Рассмотрим интерполяционный многочлен в форме Ньютона. Он имеет вид

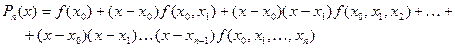(4.11)

Это многочлен степени n и при всех х ₀, х ₁ ,..., х_n имеет место соотношение

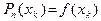в силу свойства разностных отношений (2.5):

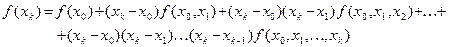
Многочлен (4.11) называется интерполяционным многочленом в форме Ньютона.

пример построения интерполяционного многочлена в форме Ньютона.

xi	f (xi)	f (xi,xi+1)	f (xi,xi+1,xi+2)
-2		-1.795	-0.410
-0.5	2.3075	-2.615

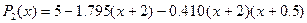Вычислим этот многочлен при x = -1:

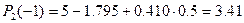
Дата добавления: 2014-01-14