Интерполирование по равноотстоящим узлам

Здесь мы воспользуемся интерполяционным многочленом в форме Ньютона, преобразовав его к форме, удобной для интерполирования по равноотстоящим узлам.

Пусть даны точки x₀ , x₁,..., x_n,принадлежащие промежутку [ a,b ] и в них значения некоторой функции f (x): f (x₀) = y₀, f (x₁) = y₁, f (x₂) = y₂ ,..., f (x_n) = y_n. Пусть нам нужно вычислить значение функции f в некоторой точке x^*, не совпадающей ни с одной из точек x_i. В зависимости от положения точки x^*, мы будем строить многочлены для начала, конца, или середины таблицы.

Рассмотрим интерполяционный многочлен в форме Ньютона вида

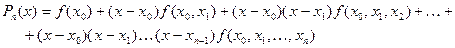
1. Начало таблицы.

Пусть точка x^* лежит между точками x₀ и x₁. Введем новую переменную t, положив . Точками интерполирования будут ближайшие к точке x^* узлы т.е. x₀, x₁,..., x_k.

x	y	Dy	D^2y		D^ny
x0	y0	Dy0	D^2y0	...	D^ny0
x1	y1	Dy1	D^2y1	...
x2	y2	Dy2	...
...	...	...	D^2yn-2
xn-1	yn-1	Dyn-1
xn	yn

Тогда интерполяционный полином в форме Ньютона будет иметь вид:

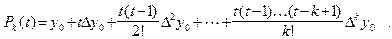(5.1)

Это интерполяционный полином в форме Ньютона для начала таблицы.

О погрешности.

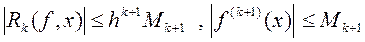
2. Конец таблицы.

Пусть точка x^* лежит между точками x_n-1 и x_n. Тогда переменная t будет определена по правилу th=x-x_n. Точками интерполирования будут точки x_n, x_n-1,..., x_{n-k .} Интерполяционный полином будет иметь вид

(5.2)

3. Середина таблицы.

Пусть точка x* расположена так, что точки таблицы находятся с двух сторон от нее. В этом случае нам придется и в качестве точек интерполирования брать точки с двух сторон от нее. Пусть ближайшей к x*, является точка x_i. Мы будем рассматривать точки... x_i-2, x_i-1, x_i,

x_i+1 , x_i+2,.... Переобозначим их для удобства, т.е.... x_-2, x_-1, x₀, x₁, x₂....

x	y	Dy	D^2y		D^ny
...	...	...	...
x-2	y-2	Dy-2	...
x-1	y-1	Dy-1	D^2y-1	...
x0	y0	Dy0	D^2y0	...	D^ny0
x1	y1	Dy1	D^2y1	...
x2	y2	Dy2	...
...	...	...	...	...
x k-1	yk-1	Dyk-1
x k	yk

Нам придется рассмотреть 2 случая.

а) x* лежит между x₀ и x₁. В этом случае узлы интерполирования расположатся следующим образом x₀, x₁, x_-1 , x₂, x_-2,.... Положим . Интерполяционный полином будет иметь вид:

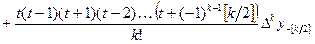(5.3)

Эта формула называется формулой Ньютона - Гаусса для середины таблицы интерполирования вперед.

б) x* лежит между x_-1 и x₀. Узлы выберем в следующей последовательности:

x₀, x_-1, x₁ , x_-2, x₂,.... Снова полагаем и получаем интерполяционный многочлен в виде:

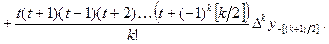(5.4)

Это формула Ньютона - Гаусса для середины таблицы интерполирования назад.

С помощью полусуммы этих двух формул можно получить формулу Стирлинга:

(5.5)

Дата добавления: 2014-01-14