Численное дифференцирование

Пусть на промежутке [a,b] дана некоторая система точек x₀ , x₁,...,x_n и в этих точках даны значения некоторой функции f (x). Ставится задача о вычислении производных от этой функции в какой-либо точке на промежутке [a,b], при условии, конечно, что функция дифференцируема нужное число раз. Эту задачу можно решить с помощью интерполяционного многочлена. Действительно, если P_n(x) - интерполяционный многочлен степени n для функции f (x), построенный по точкам x₀ , x₁,...,x_n, то можно считать производную от функции f (x) приближенно равной производной от многочлена P_n(x). Рассмотрим некоторые наиболее часто употребляющиеся формулы.

Пусть точки x₀ , x₁,...,x_n расположены на промежутке равномерно: x_i+1=x_i+h, где h - постоянный шаг. Построим таблицу конечных разностей для f (x).

x	y	Dy	D^2y		D^ny
x0	y0	Dy0	D^2y0	...	D^ny0
x1	y1	Dy1	D^2y1	...
x2	y2	Dy2	...
...	...	...	D^2yn-2
xn-1	yn-1	Dyn-1
xn	yn

Пусть мы хотим найти первую производную функции f (x) в точке 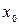. Запишем интерполяционный многочлен для начала таблицы:

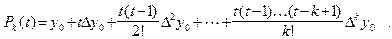
Здесь 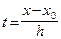, поэтому при дифференцировании по x появится множитель 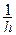.Таким образом, можно записать

Пусть у нас интерполяционный многочлен имет 1-ю степень, т.е. .

Тогда . (6.1)

Эта формула называется первой разностной производной вперед. Для вычисления первой производной функции f (x) в точке x ₁ можно снова воспользоваться многочленом .

Получим (6.2).

Эта формула называется первой разностной производной назад.

Рассмотрим погрешность каждой из полученных формул. Для погрешности интерполирования многочленом 1-й степени имеет место оценка: 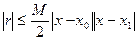, т.е. 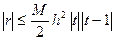. Но t<1, следовательно, ошибка интерполирования является величиной порядка h ². Тогда ошибка производной будет величиной порядка h. Таким образом, мы получили формулы для первой производной первого порядка точности. Получим теперь для 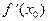формулу второго порядка точности. Возьмем интерполяционный полином для начала таблицы 2-го порядка: 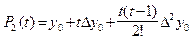. Запишем приближенно 1-ю производную для f (x) в точке x ₀: 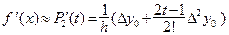, или 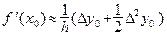, т.е.

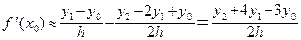. Таким образом, мы получили формулу: 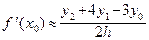. (6.3)

Это выражение называется односторонней первой разностной производной второго порядка точности. Действительно, ошибка интерполирования многочленом 2-го порядка оценивается величиной 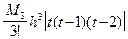, где M ₃ - положительная постоянная, ограничивающая сверху 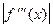на промежутке [ x ₀ , x ₂] длины 2 h.

Теперь рассмотрим центральную разностную производную 1-го порядка. Для этого запишем интерполяционный многочлен Стирлинга 1-й степени

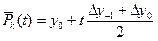. Этот многочлен построен по узлам . Продифференцируем этот многочлен: 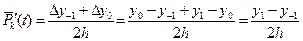. Таким образом, можно положить 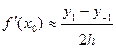. (6.4)

Погрешность этой формулы будет .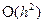

Теперь рассмотрим 2-ю производную. Возьмем интерполяционный многочлен для начала таблицы 2-й степени: 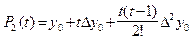. Продифференцировав его дважды, получим 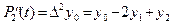. Т.е. можно положить 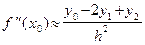. Погрешность интерполирования снова оценивается величиной 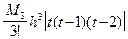, следовательно, погрешность 2-й производной будет величиной O(h). Чтобы получить для 2-й производной формулу более высокого порядка точности, рассмотрим 3 точки x_-1, x₀, x₁. Запишем интерполяционный многочлен Стирлинга 2-го порядка: 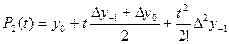. Для этого многочлена погрешность, вообще говоря, оценивается величиной 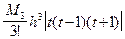, но если мы это выражение дважды продифференцируем и положим t= 0, то член, дающий оценку погрешности для производной обратится в 0, следовательно, нам нужно рассмотреть погрешность интерполяционного многочлена 3-й степени. Ее погрешность оценивается величиной . Для функции f(x) 2-я производная в точке x ₀ может быть определена по формуле 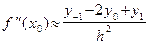. (6.5)

Погрешность этой формулы будет величиной O (h ²).

Дата добавления: 2014-01-14