Определение нормы стока по уравнению регрессии

Составляем корреляционное уравнение (уравнение регрессии) в виде

(6)

где - норма стока в изучаемом бассейне; - норма стока в бассейне аналоге;

, - средние значения годовых модулей стока в изучаемом бассейне и в бассейне аналоге за короткий период времени n лет.

- средние квадратические отклонения годовых модулей стока в изучаемом бассейне и в бассейне аналоге, подсчитанных по многолетнему ряду (N лет).

Среднее квадратическое отклонение вычисляют по формуле

(7)

В изучаемом бассейне многолетние данные наблюдений отсутствуют, поэтому для определения среднего квадратического отклонения 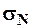, используют формулу математической статистики вида

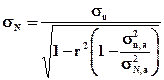
(8)

Из уравнения (6) искомая норма стока равна

(9)

Для расчета величины производим вычисления в таблице 2.

Таблица 2.

Вычисление среднего квадратического отклонения годовых модулей стока р.... у г...

за период......-...... гг.

№№ п.п.	Годы	Среднегодовые модули стока, Ма л/с.км^2	DМ=Ма-М0,а	(Ма-М0,а)^2
... ...
	Сумма

По формуле (7) находим s_N,a. Среднеквадратическоеотклонение годового стока s_N, приведенное к многолетнему периоду в изучаемом бассейне вычисляем по формуле (8). Далее, зная все члены правой части уравнения (9), определяем нормы стока в изучаемом бассейне. Относительная средняя квадратическая ошибка найденной нормы стока (М₀) вычисляется по уравнению

1(10)

2. Определение нормы стока по удлиненному ряду состоит в следующем. Выражаем связь между годовым стоком в изучаемом бассейне и в бассейне аналоге корреляционным уравнением вида

1(11)

где М и М_а - текущие координаты уравнения.

Пользуясь уравнением (11) удлиняем ряд наблюдений в изучаемом бассейне. Для этого в уравнение (11) подставляем последовательно модуль стока аналоге (М_а) и находим соответственно модуль стока в изучаемом бассейне (М) за все недостающие годы, т.е. получаем столько членов ряда, сколько имеется наблюдений в аналоге. Так, например для рассматриваемых бассейнов (изучаемым и аналогичным)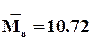 л/(с км²); r=0.98; s _n =2.325(л/ с км²)

s _n,а =2.173 л/(с км²); _n,a=10,3 л/ (с км²);

тогда

Дата добавления: 2014-01-14