
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекція 7
|
|
|
|
.
Допустим, что годовой модуль стока реки аналога в 1919 г.
Ма=10.0 л/ (с км2). Из уравнения (11) находим годовой модуль стока в изучаемом бассейне в 1919 г.
М1919= 10.72+0.98 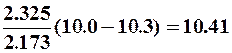 л/(с км2)
л/(с км2)
в 1920 г. Ма = 6.8 л/(с км2), тогда
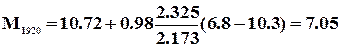 л/ (с км2)
л/ (с км2)
Аналогично определяем значение годового стока изучаемого бассейна для всех последующих лет за которые имеются наблюдения в аналоге.
По удлиненному ряду находим норму стока, как среднее арифметическое
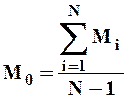
| 1(12) |
II. Определение нормы стока по графику связи. Исходные данные: годовые модули стока в изучаемом бассейне за период n=10 лет.
В данной работе бассейн-аналог указан и приведены данные наблюдений в нем за многолетний период (n=25 лет).
Данные одновременных наблюдений (за период n лет) наносятся на координатную сетку, откладывая по оси ординат годовые модули стока в изучаемом бассейне (М), по оси абсцисс - модули стока в бассейне- аналоге (Ма). По этим точкам проводим линию связи таким образом, чтобы она удовлетворяла равномерному расположению точек по обе стороны. Масштаб построения графика связи выбирают так, чтобы линия связи проходила примерно под углом 450.Для построения удовлетворительной прямолинейной связи годовых значений стока необходимо иметь одновременные наблюдения в изучаемом и аналогичном бассейне не менее 6 лет (n ³ 6 лет). Отклонение большей части точек от линии связи не должно превышать 15%.
Вычислив норму стока в бассейне аналоге непосредственно по длинному ряду наблюдений ( ), откладываем ее значения на оси абсцисс и по графику связи находим норму стока в изучаемом бассейне.
), откладываем ее значения на оси абсцисс и по графику связи находим норму стока в изучаемом бассейне.
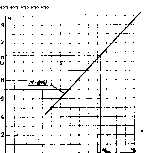
На рис. 1 приведен график связи между годовыми модулями стока р.Камы у пр. Дворянской и р. Камы у г. Перми за 1909 - 1918 гг. По норме стока аналога Мо,а=10.26 л/(с км2) графически определяем соответствующее ей значение нормы в расчетном створе (р.Кама у пр. Дворянская) Мо=10.7 л/(с.км2).
 Mn,a
Mn,a
Рис.1. График связи между годовыми модулями стока р. Камы у пр. Добрянская (М) и р. Камы у г. Пермь (М0).
III. Определение нормы стока по приближенной формуле. Норму стока по приближенной формуле определяют при очень коротком периоде наблюдений (n< 6 лет). Этот способ исходит из предположения, что линия связи стока в двух бассейнах проходит через начало координат и соотношение стока за различные периоды остается постоянным, а именно
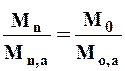
| (13) |
где Мn, Mn,a - среднее значение стока в изучаемом и аналогичном бассейне за одновременный короткий период наблюдений;
Мо, Мо,а - норма стока в изучаемом и аналогичном бассейне. Отсюда норма стока в изучаемом бассейне (с коротким периодом наблюдений) равна
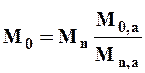
| (14) |
Формула (14) может быть использована в случае, когда отношение 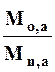 находится в пределах 0.8-1.4, а отношение коэффициентов вариации стока в изучаемом и аналогичном бассейне
находится в пределах 0.8-1.4, а отношение коэффициентов вариации стока в изучаемом и аналогичном бассейне 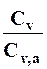 в пределах 0.8 - 1.2. Расчет по формуле (14) производим по тем же исходным данным, что и в предыдущем параграфе.
в пределах 0.8 - 1.2. Расчет по формуле (14) производим по тем же исходным данным, что и в предыдущем параграфе.
IV. Определение нормы стока при отсутствии гидрометрических данных. При отсутствии наблюдений над стоком норму стока для какой-либо неизученной реки можно приближенно определить по картам изолиний среднего годового стока. Такая карта для всего Советского Союза составлена в 1946 г. Б.Д. Зайковым.
В 1962 г. опубликована уточненная карта К.П. Воскресенским по большому количеству пунктов наблюдений и по более длинным рядам стока.
Как это было показано на рис.2, для определения нормы стока какой-либо неизученной реки на карте изолиний стока проводится водораздельная линия бассейна реки до замыкающего створа А и определяется М - центр тяжести бассейна; значение модуля стока для центра тяжести М определяется путем интерполяциии между соседними изолиниями, в рассматриваемом примере - между изо-линиями 5 и 6 л/сек с 1 км2, и получается равным 5.3 л/(с км2). Это значение и принимается в качестве нормы стока для бассейна реки до замыкающего створа А.
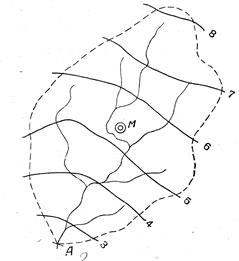
Рис.2. Определение среднего многолетнего стока по карте изолиний
модулей стока (л/сек с 1 км2).
Определив норму стока в виде модуля, можно вычислить значение среднего годового многолетнего расхода по формуле
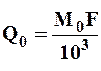 м3/сек, м3/сек,
| (15) |
где М0 - модуль стока, определенный по карте для центра тяжести бассейна, в л /сек с км2; F - площадь бассейна до данного замыкающего створа в км2.
Для очень больших речных водосборов и при различии в нормах стока на отдельных составляющих водосбора следует определять по карте изолиний средневзвешенный модуль стока по следующей формуле
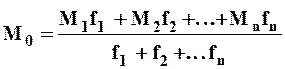 л /сек с км2 л /сек с км2
| (16) |
где М1, М2,..., Мn - средние арифметические значения модулей стока соседних изолиний, ограничивающих отдельные бассейна, f1, f2,..., fn - площади бассена между соседними изолиниями стока, определяемые планиметрированием.
Определение нормы стока по картам изолиний на Европейской территории России для больших бассейнов может быть сделано с точностью до 3-5 %; для малых бассейнов точность определения нормы стока рек значительно снижается.
Распределение нормы стока рек по территории РФ имеет ясно выраженную широтную зональность.
В заключении следует произвести сопоставление результатов расчета нормы годового стока различными способами, принимая в качестве основного способа - определение нормы стока по многолетним гидрометрическим данным.
Результаты сопоставления нормы годового стока приведены в таблице 3.
Таблица 3
Сопоставления нормы годового стока, полученные различными способами.
| Много-летний ряд | Метод корреляции --------------------------- | График связи | Приближенная формула | Карта изолиний | ||
| Уравнение регоессии | Удлиненныйряд | |||||
| М л/с.км2 | ||||||
| % отклоне-ния | - |
Лінійні неоднорідні диференціальні рівняння із сталими коефіцієнтами. Знаходження частинних розв’язків методом добору. Застосування лінійних диференціальних рівнянь до вивчення коливних явищ в електричних контурах.
Лінійними неоднорідними диференціальними рівняннями n -го порядку зі сталими коефіцієнтами називається рівняння виду
 (7.1)
(7.1)
де  – неперервна на
– неперервна на  функція,
функція,  ,
, 
Оскільки фундаментальну систему розв’язків відповідного однорідного рівняння завжди можна побудувати, то задача інтегрування рівняння (7.1) зводиться до задачі побудови якого-небудь частинного розв’язку рівняння (7.1). Частинний розв’язок рівняння (7.1) завжди можна знайти, застосовуючи метод варіації довільних сталих (Лагранжа) або метод Коші.
Розглянемо також метод добору, який дозволяє знаходити частинний розв’язок рівняння (7.1) суто алгебраїчними методами.
Якщо права частина  в (7.1) має спеціальний вид
в (7.1) має спеціальний вид
 (7.2)
(7.2)
де  – комплексна (зокрема дійсна) стала, яка називається контрольним числом функції
– комплексна (зокрема дійсна) стала, яка називається контрольним числом функції  ;
;  – многочлен степеня
– многочлен степеня  , то знаходження частинного розв’язку по суті зводиться до алгебраїчних операцій.
, то знаходження частинного розв’язку по суті зводиться до алгебраїчних операцій.
Нехай контрольне число  є коренем характеристичного рівняння оператора
є коренем характеристичного рівняння оператора  кратності
кратності  (якщо
(якщо  , то отримуємо резонансний випадок; якщо
, то отримуємо резонансний випадок; якщо  не є коренем характеристичного рівняння, то
не є коренем характеристичного рівняння, то  і отримуємо нерезонансний випадок). Тоді рівняння (1) має єдиний частинний розв’язок виду
і отримуємо нерезонансний випадок). Тоді рівняння (1) має єдиний частинний розв’язок виду
 (7.3)
(7.3)
де  – многочлен степеня
– многочлен степеня  , коефіцієнти якого можна знайти за допомогою методу невизначених коефіцієнтів.
, коефіцієнти якого можна знайти за допомогою методу невизначених коефіцієнтів.
Якщо коефіцієнти  рівняння (7.1) – дійсні числа, а права частина має спеціальний вид
рівняння (7.1) – дійсні числа, а права частина має спеціальний вид
 (7.4)
(7.4)
де  – дійсні сталі,
– дійсні сталі,  – многочлени степеня
– многочлени степеня  і
і  відповідно з дійсними коефіцієнтами, то рівняння (7.1) має єдиний частинний розв’язок виду
відповідно з дійсними коефіцієнтами, то рівняння (7.1) має єдиний частинний розв’язок виду
 (7.5)
(7.5)
де  – кратність контрольного числа
– кратність контрольного числа  функції
функції  як кореня характеристичного рівняння оператора
як кореня характеристичного рівняння оператора  (
( – резонансний випадок,
– резонансний випадок,  – нерезонансний випадок),
– нерезонансний випадок), 

 – многочлени степеня
– многочлени степеня  , коефіцієнти яких можуть бути знайдені методом невизначених коефіцієнтів.
, коефіцієнти яких можуть бути знайдені методом невизначених коефіцієнтів.
Отже, лінійні неоднорідні рівняння зі сталими коефіцієнтами завжди можна проінтегрувати в квадратурах, причому у випадку, коли права частина рівняння (7.1) – функція  має спеціальний вигляд (7.2) або (7.4), інтегрування по суті зводиться до алгебраїчних операцій.
має спеціальний вигляд (7.2) або (7.4), інтегрування по суті зводиться до алгебраїчних операцій.
Приклад 1. Знайти загальний розв’язок рівняння 
Розв’язання.
Характеристичне рівняння  має розв’язки
має розв’язки  і
і  . Загальний розв’язок відповідного однорідного рівняння
. Загальний розв’язок відповідного однорідного рівняння  Права частина даного рівняння
Права частина даного рівняння  Звідси,
Звідси,  так як
так як  і
і  . Диференціюючи
. Диференціюючи  двічі і підставляючи похідні в дане рівняння, дістанемо:
двічі і підставляючи похідні в дане рівняння, дістанемо:

Скоротивши на  і порівнявши коефіцієнти при перших степенях х і вільні члени в лівій і правій частині рівності, отримаємо 5А=4 і 7А+5В=0, звідки
і порівнявши коефіцієнти при перших степенях х і вільні члени в лівій і правій частині рівності, отримаємо 5А=4 і 7А+5В=0, звідки  і
і 
 .
.
Тоді  .
.
Приклад 2. Знайти загальний розв’язок рівняння 
Розв’язання.
Характеристичне рівняння  має двохкратний корінь
має двохкратний корінь  . Права частина рівняння має вигляд
. Права частина рівняння має вигляд  тут
тут  і
і  . Частковий розв’язок
. Частковий розв’язок  оскільки
оскільки  співпадає з двократним коренем
співпадає з двократним коренем  і, тому,
і, тому, 
Диференціюючи  два рази, підставляючи в рівняння і прирівнюючи коефіцієнти, дістаємо
два рази, підставляючи в рівняння і прирівнюючи коефіцієнти, дістаємо 
 Звідси, загальний розв’язок даного рівняння записується у вигляді
Звідси, загальний розв’язок даного рівняння записується у вигляді

Приклад 3. Знайти загальний розв’язок рівняння 
Розв’язання. Характеристичне рівняння  має розв’язки
має розв’язки  і
і  . Загальний розв’язок відповідного однорідного рівняння буде:
. Загальний розв’язок відповідного однорідного рівняння буде:

Права частина має вигляд

де 



 Їй відповідає частковий розв’язок
Їй відповідає частковий розв’язок

(тут N=1, a=0, b=1, r=1).
Диференціюючи два рази і підставляючи отримані вирази в рівняння, порівнюємо коефіцієнти в обох частинах рівності при  ,
,  ,
,  ,
,  . В результаті дістаємо систему чотирьох рівнянь:
. В результаті дістаємо систему чотирьох рівнянь:




з яких і визначаються 

 ,
,  .
.
Тому 
Загальний розв’язок

Дослідження коливних процесів за допомогою диференціальних рівнянь продемонструємо на основі прикладу.
Приклад 4. Знайти загальні розв’язки рівнянь
 (7.6)
(7.6)


 (7.7)
(7.7)
Характеристичне рівняння має корені  Праві частини рівнянь (7.6), (7.7) мають спеціальний вид (7.4), причому в обох випадках контрольне число
Праві частини рівнянь (7.6), (7.7) мають спеціальний вид (7.4), причому в обох випадках контрольне число  . Розглянемо наступні випадки.
. Розглянемо наступні випадки.
Нерезонансний випадок:  . Тоді число
. Тоді число  не є коренем характеристичного рівняння,
не є коренем характеристичного рівняння,  і частинні розв’язки шукаємо у вигляді
і частинні розв’язки шукаємо у вигляді
 (7.8)
(7.8)
 (7.9)
(7.9)
підставивши (7.8) і (7.9) відповідно в рівняння (7.6) і (7.7), отримаємо


звідси, внаслідок лінійної незалежності функцій  ,
,  , маємо
, маємо



 (7.10)
(7.10)
Беручи до уваги те, що  знаходимо
знаходимо




Тому 

Резонансний випадок:  Контрольне число
Контрольне число  є коренем характеристичного рівняння кратності
є коренем характеристичного рівняння кратності  Тоді частинні розв’язки шукаємо у вигляді
Тоді частинні розв’язки шукаємо у вигляді
 (7.11)
(7.11)
 (7.12)
(7.12)
Підставивши (7.11) і (7.12) відповідно в рівняння (7.6) і (7.7), отримаємо




Звідки 



Тому  ,
,  .
.
Контрольні запитання
1. Як розв’язуються лінійні неоднорідні диференціальні рівняння зі сталими коефіцієнтами?
2. У чому полягає метод невизначених коефіцієнтів? Поясніть на прикладі.
3. Як дослідити коливні процеси за допомогою лінійних неоднорідних диференціальних рівнянь зі сталими коефіцієнтами?
|
|
|
|
|
Дата добавления: 2014-01-14; Просмотров: 375; Нарушение авторских прав?; Мы поможем в написании вашей работы!