Безотказность характеризуется единичными количественными показателями, номенклатура которых определена ГОСТ 27.002–89

Безотказность(Reliability, failure-free operation) – свойство объекта непрерывно сохранять работоспособное состояние в течение некоторого времени или наработки.

Безотказность и ее показатели

Рассмотрим отдельные свойства надежности и их показатели.

Вероятность безотказной работы (Reliability function, survival function) 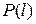– это вероятность того, что в пределах заданной наработки отказ объекта не возникнет.

Статистически вероятность безотказной работы можно определить отношением числа автомобилей, безотказно проработавших до заданной наработки, к общему числу опытных автомобилей в партии:

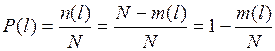, (8.1)

где n(l) – число автомобилей, безотказно проработавших до заданной наработки;

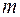(l) – число отказавших автомобилей к заданной наработке;

N – число автомобилей, работоспособных в начальный момент времени.

В начальный момент времени (перед испытаниями) все объекты являются исправными, т. е. выполняется равенство n=N и, следовательно, P(l) = 1.

Если испытания проводятся до отказа всех N объектов, то в конце испытаний n = 0, а P(l) = 0.

Следовательно, вероятность безотказной работы в течение конечных интервалов времени может иметь значения в пределах от 0 до 1 (0 P(l) 1).

Если по опытным данным определена функция распределения случайной величины, то вероятность безотказной работы может быть определена по следующей формуле:

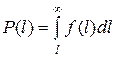. (8.2)

Если плотность вероятности распределена по нормальному закону, то:

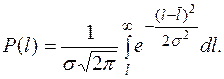(8.3)

Для распределения Вейбулла:

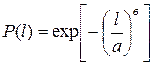. (8.4)

Для экспоненциального распределения:

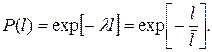(8.5)

Для логарифмически нормального распределения:

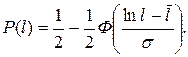(8.6)

Наряду с понятием “вероятность безотказной работы” часто используют понятие “вероятность отказа”, которое определяется следующим образом: это вероятность того, что объект в течение заданной наработки откажет хотя бы один раз, будучи работоспособным, в начальный момент времени.

Вероятность отказов – по смыслу величина, противоположная вероятности безотказной работы и связанная с функцией распределения наработки до отказа:

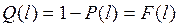, (8.7)

где F(l) – функция распределения наработки до отказа.

Статистически вероятность отказа можно определить следующим образом:

. (8.8)

Используя вероятностные характеристики, вероятность отказа определяем по формуле:

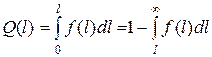. (8.9)

С увеличением наработки вероятность безотказной работы уменьшается, а вероятность отказа возрастает.

Средняя наработка до отказа (Mean operating time to failure) – это математическое ожидание наработки объекта до первого отказа.

Статистическая оценка для средней наработки до отказа определяется отношением суммы наработки испытуемых объектов до отказа к числу наблюдаемых объектов, если они все отказали за время испытаний.

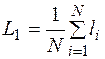, (8.10)

где N – число работоспособных объектов при l= 0;

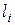– наработка до первого отказа каждого из объектов.

Если определена функция распределения плотности вероятности 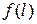, то:

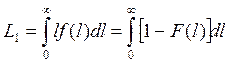, (8.11)

где 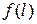– плотность распределения наработки до отказа.

Для экспоненциального закона распределения:

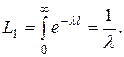(8.12)

Для логнормального закона распределения:

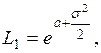(8.13)

где 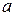– параметр распределения.

Для закона Вейбулла:

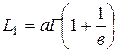, (8.14)

где Г– гамма–функция.

Средняя наработка на отказ (наработка на отказ), (Mean operating time between failures) – это отношение суммарной наработки восстанавливаемого объекта к математическому ожиданию числа его отказов в течение этой наработки.

Данному определению средней наработки на отказ 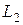соответствует следующая формула:

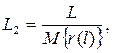(8.15)

где L – суммарная наработка;

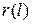– число отказов, наступивших в течение этой наработки;

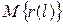– математическое ожидание этого числа.

Статистическую оценку средней наработки на отказ 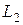вычисляют по формуле:

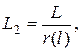(8.16)

где 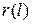– число отказов, фактически происшедших за суммарную наработку L.

Формула (8.16) допускает обобщение на случай, когда объединяются данные, относящиеся к группе однотипных объектов, которые эксплуатируются в статистически однородных условиях. Если поток отказов – стационарный, то в формуле достаточно заменить L на сумму наработок всех наблюдаемых объектов и заменить 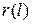на суммарное число отказов этих объектов.

Гамма – процентная наработка до отказа (Gamma – percentile operating time to failure) – это наработка, в течение которой отказ объекта не возникнет с вероятностью γ, выраженной в процентах. Обычно применяют γ = 80, 85, 90 и 95%.

Гамма – процентная наработка до отказа 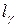определяется из уравнения:

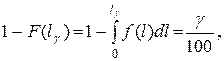(8.17)

где 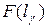– функция распределения наработки до отказа.

Интенсивность отказов (Failure rate) – условная плотность вероятности возникновения отказа объекта, определяемая при условии, что до рассматриваемого момента времени отказ не возник.

Интенсивности отказов λ (t) определяют по формуле:

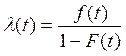. (8.18)

Статистически интенсивность отказов определяется отношением разности между числом отказов n(t + t) на момент времени (t + t) и числом отказов n(t) на момент времени t к длительности интервала времени t и количеству работоспособных объектов на момент времени t

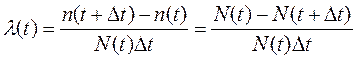, (8.19)

где N(t) и N(t+Δt) – число работоспособных элементов при наработках t и (t+Δt) соответственно.

Параметр потока отказов (Failure Intensity) – это отношение математического ожидания числа отказов восстанавливаемого объекта за достаточно малую его наработку к значению этой наработки.

Рассмотрим эксплуатацию восстанавливаемых объектов. В начальный момент времени изделие начинает работу и работает до отказа. При отказе происходит восстановление объекта, и он вновь работает до следующего отказа и т. д. Моменты отказов формируют поток отказов.

В качестве характеристики потока отказов используют математическое ожидание числа отказов за время t называемой ведущей функцией потока отказов W (t) (функция восстановления).

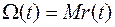. (8.20)

Математическое ожидание числа отказов за интервал времени (t₁, t₂) определяют по формуле:

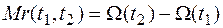, (8.21)

где r(t₁, t₂) – число отказов за интервал времени (t₁, t₂).

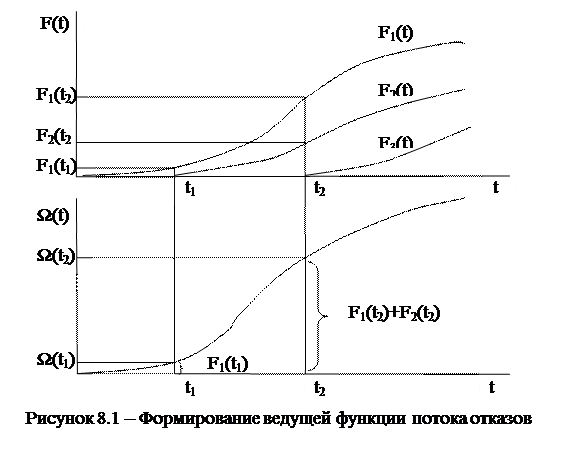
Как видно из рисунка 8.1, из-за вариации наработок на отказ происходит их смещение, а функции вероятностей первых и последующих отказов частично накладываются друг на друга. Например, для момента времени t₂ общее количество отказов определяется суммированием вероятностей первого F₁(t₂) и второго F₂(t₂) отказов. Исходя из этого, ведущая функция потока отказов формируется следующим образом:

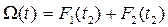. (8.22)

А в общем случае:

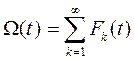. (8.23)

Параметр потока отказов ω(t) определяют по формуле:

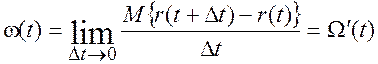, (8.24)

где Δ t – малый отрезок наработки;

r(t) – число отказов, наступивших от начального момента времени до достижения наработки t.

Разность r(t+Δt) - r(t) представляет собой число отказов на отрезке Δt.

Иными словами, параметр потоков отказов (t) – это относительное количество отказов, приходящихся на единицу времени или пробега одного изделия.

Осредненный параметр потока отказов (Mean failure Intensity) – это отношение математического ожидания числа отказов восстанавливаемого объекта за конечную наработку к значению этой наработки.

Дата добавления: 2014-01-14