
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Модели дискретной обработки информации
|
|
|
|
Построение класса примитивно-рекурсивных функций
Рассмотрим, каким образом может быть построен класс рекурсивных функций.
Определение. Функция y=j (x1, x2,..., xn) называется алгоритмически вычислимой (просто вычислимой), если существует алгоритм, позво-ляющий определить значение функции y при любых значениях пере-менных х1, х2,..., хn.
Определение. Предикат Р (х1, х2,..., хn), определённый на множестве целых чисел, называется алгоритмически разрешимым (просто разреши-мым), если существует алгоритм для определения значений предиката Р при любых значениях переменных х1, х2,..., хn.
Эти определения являются неточными, поскольку ещё не сформули-ровано точно понятие алгоритма. Для их уточнения построим класс вычис-лимых функций, начав с элементарных. Элементарными являются все функции вида
j(x) = x+ 1, j (y) = 12 y, y (a, b, c) =ab+c, l (b) =bn и т.п.
Рассмотрим эти функции подробнее. Если в функции j (x) =x+ 1 поло-жить x= 0 (начальное значение) и затем многократно использовать эту формулу с предыдущим значением, то таким путём можно получить все числа натурального ряда. Многократное применение одной и той же формулы (вычислительного процесса) называют итерацией. Операцию сложения двух чисел a+b можно представить как применение формулы x+ 1 b раз, если в качестве начального значения x положить a; таким образом, сложение двух целых чисел - это итерация добавления единицы. Нетрудно видеть, что произведение an=a+a+...+a - n раз повторенное сложение (умножение - итерация сложения).
Функция y может быть представлена в виде y=d+c, где d=ab, так что y включает в себя две операции: умножение как итерацию сложения и операцию сложения как итерацию добавления единицы (в последнем случае полагаем d начальным значением для x - см. функцию f). Все эти функции растут довольно медленно, и по этому признаку их относят к элементарным.
Рассмотрим операцию возведения в степень. Для функции l (b) име-ем bn= bb...b - n раз повторенное умножение на число b, т. е. это итерация умножения: bn =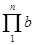 . Эта функция, хотя и растёт довольно быстро, является ещё элементарной, так как она выражается через произведение.
. Эта функция, хотя и растёт довольно быстро, является ещё элементарной, так как она выражается через произведение.
Построим еще более быстро растущую функцию, которая является итерацией возведения в степень: y (0, a) =a, y (1, a)=aa, y (2, a)=a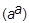 и в общем виде
и в общем виде
y(n+ 1, a) =a y (n,a). (2.1)
Функция (2.1) растёт чрезвычайно быстро; эта функция, начиная с некоторого а=а*, мажорирует все элементарные функции, т. е. для любой элементарной функции j (a) найдётся такое число n*, что будет выполняться неравенство j (а) <y (n*, a) для всех а 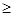 а*.
а*.
Таким образом, итерация возведения в степень позволяет получить неэлементарную функцию. В то же время y (n, a) заведомо вычислима. Действительно, пусть необходимо вычислить значение y (n, a) при любых n=n*, a=a*. При a=a* формула (2.1) даёт
y (n+ 1, a*) = (a*) y(n, a*) . (2.1’)
Обозначим (a*) m= l (m); l (m) - элементарная, всюду однозначно вы-числимая функция. Алгоритм её вычисления сводится к повторенному m раз умножению на a*.
Запись (см. (2.1’))
y (n +1 ,a*) =l (y (n ,a*))(2.2)
связывает значение функции y в данной точке с её значением в преды-дущей точке.
Достаточно теперь задать начальное значение y (0, a*) = a*, чтобы получить вычислительную процедуру, которая последовательно даёт сле-дующие значения:
y (1, a*) = l (y (0, a*)) = l (a*),
y (2, a*) = l (y (1, a*)) = l (l (a*)),...
Этот процесс следует продолжать, пока не будет достигнуто зна-чение y (n*, a*).
Очевидно, этим способом функция y определена всюду и однознач-но, так как вычисление её значений сводится к вычислению значений функции l(m), которая является всюду определённой и однозначной.
Рассмотрим подробнее способ определения функции y (n, a). Эта функция была задана по индукции: было задано начальное значение фун-кции y (0, a) и был указан способ вычисления её значения по предыдущим значениям с помощью допустимыхопераций. Как видим, был применён метод математической индукции. Используем этот метод в качестве основы для определения вычислимой функции. Но сперва несколько уточним и расширим схему определения по индукции.
Обозначим через x¢ функцию “ следовать за ”, которая означает пере-ход к следующему элементу заданного множества; для множества нату-ральных чисел функция x¢ совпадает с x +1. Общую схему определения вычислимой функции j (x) теперь можно уточнить таким образом:
1) задано j (0);
2) для любого x указывается, каким образом значение j (x¢) выражается в терминах x и j (x):
j (0) =q, j (x¢) =l (x,j (x)). (2.3)
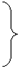 В более общем случае в функции j могут присутствовать ещё и неизменяемые в процессе индукции параметры x2, x3,..., xn (обозначим (
В более общем случае в функции j могут присутствовать ещё и неизменяемые в процессе индукции параметры x2, x3,..., xn (обозначим (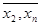 ). Схема (2.3) тогда будет иметь вид
). Схема (2.3) тогда будет иметь вид
j (0 ,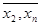 )= y (
)= y (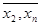 )
)
j (x¢1, 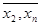 )= l (x1, j (x1,
)= l (x1, j (x1, 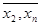 ),
), 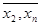 ). (2.4)
). (2.4)
Если фунции y и l известны и вычислимы, то с помощью схемы (2.4) для заданных x2=x2*, x3=x3*,... может быть организована процедура вычисления последовательно j (1,  ), j (2,
), j (2,  )и т. д. Значит, схема, заданная выражениями (2.4), действительно определяет вычислимую функцию.
)и т. д. Значит, схема, заданная выражениями (2.4), действительно определяет вычислимую функцию.
Добавим к описанной выше функции x¢ также функцию-константу и функцию-тождество. Эти три функции будем считать первоначально изве-стными, или просто первоначальными.
Итак, получены такие первоначальные функции:
I. j(x)=x¢ - описанная выше функция следования, применённая для множества натуральных чисел.
II. j (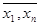 ) =q - функция-константа.
) =q - функция-константа.
III. j (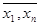 ) =xi - функция-тождество.
) =xi - функция-тождество.
Далее включим в число допустимых операций схему подстановки:
IV. j (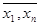 ) =y (l1(
) =y (l1(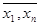 ), l 2 (
), l 2 (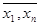 ) ,..., l m (
) ,..., l m (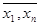 )).
)).
И наконец, введём в систему допустимых операций схемы (2.3) и (2.4) определения вычислимой функции:
V a - соответствует схеме (2.3);
V b - соответствует схеме (2.4).
Итак, схемы I-III задают первоначальные функции (они играют роль аксиом), а IV и V - правила вывода. Применяя многократно эти схемы, можно построить обширный класс вычислимых функций.
Определение. Функция j (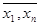 ) называется примитивно-рекурсив-ной, если она может быть построена с помощью конечного числа приме-нений схем I-V.
) называется примитивно-рекурсив-ной, если она может быть построена с помощью конечного числа приме-нений схем I-V.
Это определение раскрывает механизм построения класса прими-тивно-рекурсивных функций; этот класс включает в себя подкласс всех элементарных функций.
Отметим, что с помощью примитивной рекурсии могут быть опреде-лены конечные суммы и произведения вида
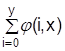 и
и 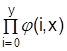 .
.
Рассмотрим пример построения примитивно-рекурсивной функции.
Пример 2.2. Определим функцию j (y, x) так:
j (0, x) =x, (A) j (y¢, x) = (j (y, x))¢ (B)
Согласно этой схеме имеем
j (1, x) = (j( 0, x))¢ = x¢ = x+ 1,
j (2, x) = (j (1, x))¢ = (x +1)¢ = x +1+1 = x +2,
j (3, x) = (j (2, x))¢ = (x +2)¢ = x +3, и вообще j (y, x) =x + y.
Назовём представляющей функцией предикатаP(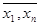 )такую функцию j (
)такую функцию j (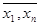 ), которая обращается в нуль лишь для тех и только тех x1, x2,..., xn, для которых P(
), которая обращается в нуль лишь для тех и только тех x1, x2,..., xn, для которых P(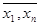 )истинно. Тогда истинностьP(
)истинно. Тогда истинностьP(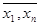 )соответствует равенству j (
)соответствует равенству j (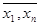 ) = 0.
) = 0.
Определение. Предикат называется примитивно-рекурсивным, если су-ществует примитивно-рекурсивная функция, представляющая этот предикат.
Из сущности механизма построения класса примитивно-рекурсивных функций видно, что каждая примитивно-рекурсивная функция является вычислимой. Верно ли обратное утверждение: всякая вычислимая функция - примитивно-рекурсивная? Иначе: все ли вычислимые функции охватывает этот механизм? Ответ на этот вопрос даётся в подразд. 2.2.2.
2.2.2. Построение класса общерекурсивных функций
Математиками были предприняты попытки построения вычислимых функций, не являющихся примитивно-рекурсивными, и такие функции бы-ли получены. Это позволило сделать вывод, что класс примитивно-рекур-сивных функций не охватывает всех вычислимых функций и нуждается в расширении. Однако нас ограничивает, прежде всего, принятая форма индукции (схема V), которая определяет функцию j через уже известные функции l и y.
Пример 2.3. Вычислим для примера 2.2 значение j (3, 5). Формально проанализируем, какие операции нужно совершить, чтобы, пользуясь схемой (A) и (B), вычислить j (3, 5).
1. Подставим в (B) вместо переменных числа n =2, x =5. Получим
j (3, 5)= j (2, 5)+1.
2. Подставим в (B) n =1, x =5 и определим j (2, 5): j (2, 5)= j (1, 5)+1.
3. Аналогично получим j (1, 5)= j (0, 5)+1.
4. Подставим в (A) x =5. Получим j( 0, 5)=5.
5. Заменим в выражении п. 3 j (0, 5) на 5, согласно п. 4:
j (1, 5)=5+1=6.
6. Заменив j (1, 5) в выражении п. 2 её значением из п. 5, получим
j (2, 5)=6+1=7.
7. Наконец, заменив j (2, 5) в выражении п. 1 её значением из п. 6, получим j (3, 5)=7+1=8.
В этом примере для организации вычислений понадобились лишь две операции:
1) подстановка чисел на место переменных;
2) замена вхождений, т. е. замена правой части в одном из равенств левой частью другого равенства (или наоборот).
Если некоторое равенство может быть выведено с помощью этих двух операций из заданной системы равенств Е, то говорят, что это равенство выводимо в системе Е. В примере 2.2 системой Е является само описание функции j (n, x).
Определение. Функция j(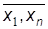 ) называется общерекурсивной, если существует такая конечная система равенств Е, что для любого набора чисел
) называется общерекурсивной, если существует такая конечная система равенств Е, что для любого набора чисел 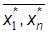 найдётся такое одно и только одно число y*, что равенство j (
найдётся такое одно и только одно число y*, что равенство j (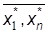 ) =y* может быть выведено из Е с помощью конечного числа применений операций подстановок чисел на место переменных и замены вхождений.
) =y* может быть выведено из Е с помощью конечного числа применений операций подстановок чисел на место переменных и замены вхождений.
Говорят, что Е рекурсивно определяет функцию j. Здесь не требует-ся, чтобы значения функции вычислялись с помощью её значений в пре-дыдущих точках; не требуется, чтобы входящие в систему Е вспомо-гательные функции были всюду вычислимы; не фиксируется никакая схема индукции. Требуется только, чтобы система равенств Е так определяла данное значение j с помощью других значений j и некоторых значений вспомогательных функций, чтобы j во всех точках можно было однозначно вычислять на основании системы Е.
Приведенное определение общерекурсивной функции не конструк-тивно, так как не раскрывает механизма вычислительной процедуры на-хождения числа y*. Можно, конечно, попробовать выводить из Евсе воз-можные равенства до тех пор, пока не встретится нужное равенство. Однако при таком подходе нет никакой гарантии, что этот процесс перебора не продлится неопределённо долго (ср. с лабиринтом).
Процессу перебора можно придать определённую регулярность, так чтобы этот процесс годился для вывода равенства j (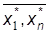 ) =y* за конеч-ное, но не ограниченное заранее число шагов.
) =y* за конеч-ное, но не ограниченное заранее число шагов.
Предварительно отметим, что равенство j (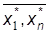 ) =y* может быть представлено в эквивалентной форме y (
) =y* может быть представлено в эквивалентной форме y (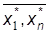 , y) = 0. Последнее равенство в общем случае имеет вид y (
, y) = 0. Последнее равенство в общем случае имеет вид y (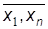 , y) = 0; этому выражению может быть поставлен в соответствие предикат P(
, y) = 0; этому выражению может быть поставлен в соответствие предикат P(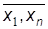 , y), истинный в случае y =0.
, y), истинный в случае y =0.
Гёдель предложил метод сведения любого алгоритма к численному алгоритму путём специальным образом организованной нумерации любых выражений (своеобразной их кодировки). Этот метод носит название гёделизации. Рассмотрим этот метод.
Включим все условия задачи, доступные для переработки данным алгоритмом A, в занумерованную неотрицательными целыми числами последовательность A0, A1, …, An. Аналогично записи возможных решений также включим в занумерованную последовательность B0, B1,..., Bm.
Теперь можно любой алгоритм, перерабатывающий запись условий An в запись решения Bm, свести к вычислению значений некоторой число-вой функции m = j (n), т.е. можно говорить об алгоритме, который перера-батывает номер записи условия в номер записи решения. Этот алгоритм будет численным алгоритмом. Очевидно, что если есть алгоритм, реша-ющий исходную задачу, то имеется и алгоритм вычисления соответ-ствующей функции. Справедливо и обратное утверждение.
Гёдель предложил рассматривать запись некоторого числа n в фор-ме n =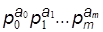 , где p0 =2, p1 =3, p2 =5 и вообще pm - m -е простое число.
, где p0 =2, p1 =3, p2 =5 и вообще pm - m -е простое число.
Из этой записи видно (в силу теоремы о единственности разложения любого числа на простые множители), что каждому числу n однозначно соот-ветствует набор a1, a2,.., am и, наоборот, каждому набору a1, a2,..., am однозначно соответствует число n. Например, при n =60 имеем: 60 = 22 31 51, т.е. a1 = 2, a2 = 1, a3 = 1.
C помощью этого метода можно нумеровать теперь любые упоря-доченные последовательности, состоящие из m чисел. Рассмотрим следующие примеры.
1. Каждой паре чисел a1 и a2, для которой нужно найти её наибольший общий делитель q, может быть поставлен в соответствие гёделевский номер этой пары n =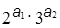 .
.
Алгоритм Евклида сведётся тогда к вычислению функции q = j (n).
2. Пусть требуется занумеровать все слова в некотором алфавите A. Это легко сделать, поставив в соответствие каждой букве алфавита какое-либо число. Тогда каждому слову в алфавите A будет соответствовать последовательность чисел. Проводя затем обычным способом гёделизацию, получим гёделевский номер этой последовательности. Ясно, что номер слова определяется выбранной системой соответствий между буквами и числами. Теперь легко пронумеровать все последовательности слов (например, все дедуктивные цепочки). Здесь также имеется однозначное соответствие последовательности слов и последовательности гёделевских номеров этих слов. Проведя гёделизацию вторично, можно определить гёделевский номер самой последовательности гёделевских номеров отдельных слов.
Итак, с помощью гёделизации арифметические алгоритмы сводятся к вычислению значений целочисленных функций. Аналогично любой нормаль-ный алгоритм Маркова может быть также сведен к вычислению значений целочисленных функций. Поэтому алгоритм вычисления значений целочис-ленных функций можно считать универсальной формой алгоритма.
Оказывается, что путём гёделизации процесс перебора всех выводов из Е (см. с. 68) сводится к применению оператора наименьшего числа m. Введение в рассмотрение этого оператора приводит к иному способу определения рекурсивных функций.
Оператор наименьшего числа m ставит в соответствие примитивно-рекурсивному предикату P(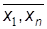 , y)(или примитивно-рекурсивной функ-ции y (
, y)(или примитивно-рекурсивной функ-ции y (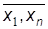 , y), представляющей предикатP) примитивно-рекурсивную функцию j (
, y), представляющей предикатP) примитивно-рекурсивную функцию j (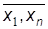 ) следующим образом:
) следующим образом:
j (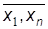 ) =my| P(
) =my| P(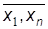 , y) = m y | y (
, y) = m y | y (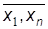 , y) =0 (2.5)
, y) =0 (2.5)
при условии
(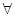 x1)(
x1)(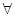 x2) ... (
x2) ... (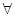 xn)(
xn)(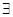 y) | P(
y) | P(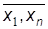 , y),(2.6)
, y),(2.6)
или
(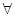 x1)(
x1)(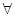 x2) ... (
x2) ... (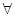 xn)(
xn)(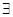 y) |y (
y) |y (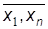 ,y) =0. (2.7)
,y) =0. (2.7)
Утверждение. Любая общерекурсивная функция j (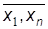 ) может быть представлена в виде
) может быть представлена в виде
j (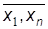 ) =t (my|y (
) =t (my|y (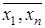 ,y) = 0), (2.8)
,y) = 0), (2.8)
где y и t - примитивно-рекурсивные функции, причём для функции y справедливо выражение
(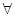 x1)(
x1)(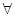 x2) ... (
x2) ... (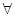 xn)(
xn)(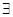 y) |y (
y) |y (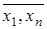 ,y) = 0. (2.9)
,y) = 0. (2.9)
Типичной ситуацией применения m -оператора является построение обратных функций. Допустим, что для некоторой функции y=f(x) существу-ет обратная функция, т. е. для каждого натурального y существует един-ственное значение x, для которого f (x) =y; в таком случае обратная функция x=j (y) может быть определена посредством m -оператора:
j (y) = m x |f (x) =y. (2.10)
Многие функции анализа, такие как показательная cx и степенная xc, определены на всём натуральном ряде, если параметр c выбран подхо-дящим образом. Однако этого нельзя утверждать об обратных функциях; например, logcx или 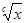 , в общем случае не будет натуральным числом даже при натуральном c. В таких случаях удобно рассматривать арифме-тические варианты обратных функций, которые заключаются в следу-ющем: в качестве значений функции объявляется целая часть истинных значений функции, т. е.] j(y) [, где ] x [ - целая часть числа x. Теперь ясно, что, исходя из функции у=cx или y=xc, можно определить арифметические обратные функции посредством m- оператора:
, в общем случае не будет натуральным числом даже при натуральном c. В таких случаях удобно рассматривать арифме-тические варианты обратных функций, которые заключаются в следу-ющем: в качестве значений функции объявляется целая часть истинных значений функции, т. е.] j(y) [, где ] x [ - целая часть числа x. Теперь ясно, что, исходя из функции у=cx или y=xc, можно определить арифметические обратные функции посредством m- оператора:
] logr (y)[ =mx | rx+1>y;
] 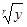 [ =mx | (x+1) r > y.
[ =mx | (x+1) r > y.
Рекурсивное описание называется примитивно-рекурсивным, если в нём не участвует m -оператор, т. е. допускаются только операторы супер-позиции, введения фиктивных переменных и примитивной рекурсии.
Если к уже известным схемам определения примитивно-рекурсивных функций добавить схему VI, составленную из (2.8) и (2.9), то в результате конечного числа применений схем I-VI получим общерекурсивную функцию j (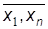 ).
).
Таким образом, примитивно-рекурсивные функции являются частным случаем общерекурсивных функций; всякая примитивно-рекурсивная фун-кция есть общерекурсивная функция, но не наоборот.
|
|
|
Дата добавления: 2014-01-14; Просмотров: 395; Нарушение авторских прав?; Мы поможем в написании вашей работы!