Конечные автоматы. Автомат - это математическая абстракция, которая предназначена для описания и анализа поведения разнообразных устройств дискретного действия или протекания

Автомат - это математическая абстракция, которая предназначена для описания и анализа поведения разнообразных устройств дискретного действия или протекания процессов дискретной обработки информации, для моделирования и построения устройств и процессов. Такая модель успешно используется как в технике (проектирование вычислительных машин, систем управления и связи), так и в других областях деятельности человека - теории и практике административного управления, лингвистике (анализ синтаксиса формального языка, расшифровка древних рукописей) и т. д. Универсальность теории автоматов позволяет рассматривать с единой точки зрения различные объекты, учитывать связи и аналогии между ними, переносить результаты из одной области в другую.

Автомат описывается шестёркой элементов А=(Q, X, Y, d, l, q₁),

где Q = { q₁, q₂,..., q_r } - множество состояний (алфавит состояний);

X = { x₁, x₂,..., x_n } - множество входных символов (входной алфавит);

Y = { y₁, y₂,..., y_m } - множество выходных символов (выходной алфавит);

d - функция переходов, реализующая отображение множества D_d,

D_dÍQ´X, на множество Q (q_p = d (q_j, x_j), q_p ÎQ);

l - функция выходов, реализующая отображение множества D_l, D_lÍQ´X, на множество Y (y_d = l (q_j, x_i), y_d Î Y);

q₁ - начальное состояние автомата.

В общем случае автомат может иметь некоторое количество входов и выходов, и тогда каждому входу и каждому выходу может соответствовать свой алфавит. Рассмотрим более простой случай автомата с одним входом и одним выходом.

Автомат называется конечным, если конечны множества Q, X и Y. Автомат называется полностью определённым, если D_d=D_l=Q´X; у частичного автомата функции d и l определены не для всех пар (q_j, x_i)ÎQ´Y.

Символами x_i и y_k обозначают события в процессе или сигналы в устройствах. Иногда используют вместо понятия “символ” понятие “ буква ”; а последовательность букв называют словом.

В отличие от привычного рассмотрения времени (время непрерывно и задается на континууме), при изучении и проектировании автоматов удобно рассматривать воображаемое дискретное время (автоматное время, заданное на счётном множестве). Разобьём непрерывную числовую полуось на бесконечное число конечных интервалов, не обязательно равных между собой, и обозначим точки, разделяющие интервалы, неотрицательными целыми числами, начиная с 0 (рис. 2.1,а).

Будем называть дискретным временем t время, которое принимает лишь эти целочисленные значения. Моменты времени, обозначенные числами 0,1,2,..., будем называть тактами.

Отметим, что в реальных условиях сигналы представляются непрерывными функциями времени, поэтому для надежного различения сигналов требуется, чтобы новые значения на входах появлялись после окончания переходных процессов, связанных с предыдущими значениями. При рассмотрении логической структуры автоматов обычно отвлекаются от существа этих процессов и считают, что переменные изменяются мгновенно в тактовые моменты.

Кроме входных и выходных переменных, можно выделить некоторую совокупность промежуточных переменных, которые связаны с внутренней структурой автомата; именно они характеризуют состояние конечного автомата (КА).

При рассмотрении КА значения символов состояний и входов существенны лишь в моменты тактов и несущественны - в промежутках между ними. Поэтому эту модель можно использовать и для описания непрерывных устройств (процессов), если фиксировать значения символов состояний и входов в моменты тактов; при этом важно, чтобы в рассматриваемые дискретные моменты множество возможных состояний было конечным и чтобы удовлетворялось требование однозначной связи между состояниями в соседних тактах.

Понятие “ состояние автомата ” определяет некоторую предысторию его поведения как реакции на символы, которые поступали ранее на его входы, т. е. состояние соответствует некоторой памяти о прошлом.

Строгое определение понятия состояния связывается с той ролью, которую оно играет при определении конечных автоматов. Во-первых, значение выходной переменной на p -м такте (p -present-настоящее) y (p) однозначно определяется состоянием q (p) и значением входной переменной x (p) на том же такте, т. е. y (p)= l (q (p), x (p)). Во-вторых, состояние q (p +1) в следующем, (p +1)-м такте, однозначно определяется состоянием q (p) и входной переменной x (p) в рассматриваемом такте - q (p +1)= d (q (p), x (p)).

Таким образом, состояние КА в любой тактовый момент характеризуется значением такой переменной, которая вместе с заданным значением входной переменной позволяет определить выходную переменную в данный тактовый момент и состояние в следующий тактовый момент.

Ясно, что автоматы должны обладать способностью сохранять предыдущее состояние до следующего такта, в связи с чем их называют автоматами с памятью (последовательностными машинами). В качестве памяти могут использоваться элементы задержки, на выходах которых повторяются входные воздействия со сдвигом во времени на интервал между тактами Dt.

Термин “состояние” позволяет устранить время как явную переменную и выразить выходные символы как функцию состояний автомата и входов в данный момент (такт). В каждый момент t =0,1,2,... дискретного времени КА находится в определённом состоянии q (t) из множества Q состояний автомата, причём в начальный момент t =0 он всегда находится в начальном состоянии q (0)= q₁. В момент p (рис. 2.1,б), находясь в состоянии q (p), КА способен воспринять на входе символ x (p)ÎX и выдать на выходе сигнал y (p)= l (q (p), x (p)), переходя в состояние q (p +1)= d (q (p), x (p),); q (p)ÎQ, y (p)ÎY.

Таким образом, КА реализует некоторое отображение j множества слов входного алфавита X во множество слов выходного алфавита Y: если на вход автомата, установленного в начальное состояние q₁, подавать некоторую последовательность букв входного алфавита x (0), x (1), x (2),..., т. е. входное слово, то на выходе КА будут последовательно появляться буквы выходного алфавита y (0), y (1), y (2),..., т. е. выходное слово. Относя к каждому входному слову соответствующее ему выходное слово, получим отображение j, индуцированное конечным автоматом.

Автомат без памяти называется тривиальным автоматом, или комбинационной схемой. В таких автоматах значения выходных переменных определяются только комбинацией входных переменных в данный момент; для комбинационных схем функция переходов не имеет смысла, а функция выходов вырождается к виду y (p)= l (x (p)).

На практике наибольшее распространение получили автоматы Мили и Мура, приведенные на рис. 2.1, в и г; здесь: F1 и F2 - комбинационные схемы; D - задержка на один такт (память), q’ - новое (следующее) состояние в момент t = p.

Закон функционирования автомата Мили задается уравнениями:

q (t +1) = d(q (t), x (t)); y (t) = l (q (t), x (t)), t = 0, 1, 2,..., (2.11)

а автомата Мура -

q (t +1) = d (q (t), x (t)); y (t) = l (q (t)), t = 0, 1, 2,..., (2.12)

Отметим особенности функционирования автоматов Мили и Мура:

· оба автомата одинаково формируют новое состояние (q, x)® q’, которое затем задерживается на один такт, q (p +1) = q’ (p);

· выходной символ в автомате Мили определяется непосредственно входным символом и состоянием в текущий момент t = p ((q, x)® y), а в автомате Мура - только состоянием в текущий момент (q ® y) и опосредованно - состоянием и входным символом в предыдущий момент t = p -1 (y(p)=l(q (p)), где q (p)= d (q (p -1), x (p -1)));

· поскольку в автомате Мура выходной символ однозначно определяется его состоянием, то это позволяет идентифицировать состояние автомата по символам на его выходе, т. е. проверять правильность функцио-нирования синтезированного автомата;

· автомат Мили обычно проще (в смысле меньшего числа состояний) эквивалентного ему автомата Мура.

При анализе и синтезе КА используются в основном две стандартные формы представления автомата: табличная и графическая. Рассмотрим эти формы.

Автомат может быть представлен двумя таблицами для каждой из функций d и l либо совмещённой таблицей, несколько отличающейся для автоматов Мили и Мура.

При табличном представлении строки именуются символами состояний, а столбцы - символами входа; в клетках таблиц проставляются символы состояний, причём состояния записываются рядом через разделитель “/” с соответствующими выходными символами: для автомата Мили - в клетках, а для автомата Мура - в именующем столбце.

Для примера табл. 2.1 описывает поведение автомата Мили, а табл. 2.2 - автомата Мура.

Таблица 2.1 Таблица 2.2

A1	x1	x2		A2	x1	x2
q1	q2/y1	q3/y2	q1/ y1	q2	q4
q2	q3/y3	---	q2/y1	q5	q2
q3	q4/y3	q2/y1	q3/y3	q5	q2
q4	---	q2/y2	q4/y2	q3	q1
	q5/y3	q3	q1

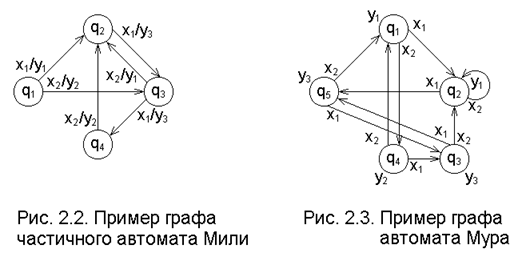
Граф автомата - ориентированный связный граф, вершины которого соответствуют состояниям, а дуги - переходам между ними. Две вершины графа автомата q_i и q_j (исходное состояние и состояние перехода) соединяются дугой, направленной от q_i к q_j, если в автомате есть переход q_i ® q_j, т. е. если q_j = d (q_i, x_k) при некотором x_k ÎX. В случае автомата Мили дуге графа приписываются входной символ x_k и выходной символ y_g = l (q_i, x_k), Если некоторые состояния автомата не определены, то в соответствующих клетках таблицы ставится прочерк; в этом случае автомат является частичным. Если переход q_i ® q_j происходит под действием нескольких входных символов, то дуге (q_i, q_j) приписываются все эти входные и соответствующие выходные символы. При описании автомата Мура в виде графа выходной символ y_g = l (q_j) записывается рядом с вершиной q_j (или внутри неё).

На рис. 2.2 и 2.3 приведены заданные ранее табл. 2.1 и 2.2 графы автоматов А1 (частичный автомат Мили) и А2 (автомат Мура; здесь переход q₂ ® q₂ является петлёй).

Дата добавления: 2014-01-14