Машина Тьюринга, её свойства и особенности

Во введении были отмечены интуитивно очевидные требования к алгоритмам: детерминированность, массовость и результативность. При этом не важно, как алгоритм реализуется: человеком или машиной. Из отличительных свойств алгоритмов вытекают общие требования к машине, выполняющей алгоритм:

· машина должна быть полностью детерминированной и действовать в соответствии с заданной системой правил;

· машина должна допускать ввод различных начальных данных, соответствующих различным задачам из заданного класса задач.

· заданная система правил работы машины и класс решаемых задач согласованы так, чтобы всегда можно было "прочитать" результат работы машины.

Предложены различные конструкции машин, способные выполнять алгоритмы. Наиболее наглядную конструкцию предложил английский математик Тьюринг (рис. 2.4,а).

Машина содержит бесконечную одномерную ленту, которая разде-лена на ячейки. Будем считать, что лента бесконечна лишь в одном на-правлении (вправо), так что существует ячейка, про которую можно ска-зать, что она нулевая (самая левая). В каждой ячейке может быть записан лишь один символ x_i из конечного алфавита X={ x₀, x₁, ..., x_n }; символ x₀ выделяем специально: если в некоторой ячейке записан символ x₀, то эта ячейка "пустая". В дальнейшем будем считать, что непустых символов на ленте каждый раз имеется конечное (но сколь угодно большое) число, остальные ячейки - пустые. Символом # отмечается левый конец ленты.

В конструкцию МТ входит также специальное устройство, содержащее считывающую и записывающую головку (далее - просто головка), которая может располагаться над любой из ячеек ленты и по команде извне может "стереть" записанный в этой ячейке символ и записать новый.

Головка может также по команде u ÎU = { R, L, S} перемещаться на одну позицию вправо (R- Right) или влево (L-Left), если она не находится в самой левой ячейке, либо не перемещаться (S – Stop). Команды на головку подаются от управляющего устройства, которое в свою очередь получает от головки сигнал о наличии того или иного символа в ячейке ленты, расположенной под головкой.

Управляющее устройство (УУ) машины Тьюринга – это конечный автомат, который имеет конечное число состояний (m +1 ) из множества Q={q₀, q₁,..., q_m} и работает в дискретном времени t = 0,1,2…. Структурная схема УУ как автомата приведена на рис 2.4,б; здесь F1, F2, F3 –комбинационные схемы (преобразователи дискретной информации без памяти); D1, D2 – элементы задержки символа (сигнала) на один такт.

Нетрудно видеть, что блоки F1, D1, F2 образуют автомат Мили (рис. 2.1,б), который формирует новый символ x, x ÎX, для записи на ленте, а дополнительные к ним блоки F3, D2 формируют команду u ÎU на перемещение головки.

Машина Тьюринга (точнее, её УУ) описывается, как и автомат, шестёркой T = (Q, X, Y, d, l, q₁), однако в данном случае имеются особенности. Выходной алфавит Y и функция выхода l имеют смысл, отличный от аналогичных элементов шестёрки автомата: символы выходного алфа-вита Y машины составлены из пар X´Y, YÍX´U, функция выхода состав-лена из двух подфункций l =(l₁, l₂), так что (q, x) y =(x, u) или (q, x) 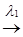x, (q, x) u, где u – символ из алфавита U = { R, L, S}.

Рассмотрим функционирование машины Тьюринга.

Входным данным для УУ является символ x_i, считываемый головкой с текущей ячейки с номером l.

Выходными данными для УУ являются: символ x_k, который головка должна записать в ячейку, а также команда u из алфавита U.

Пусть в момент t головка находилась напротив второй ячейки l, в которой был записан символ x_i, а управляющее устройство находилось в состоянии q_j. УУ в зависимости от пары символов (q_j, x_i,) выдаёт символ x_k (т.е. головка стирает старый символ x_i и записывает новый символ x_k), а затем - один из символов перемещения головки R, L, S. После этого УУ переходит в новое состояние q_r (также однозначно определяемое парой символов (q_j, x_i,)). Тем самым в момент t +1 в l -ой ячейке будет записан символ x_k, УУ будет находиться в состоянии q_r, а головка расположится напротив l +1, l -1 или l -ой ячейки.

Важно отметить, что МТ работает последовательно, т. е. последовательно обрабатывает ячейку за ячейкой (данные, записанные в них) в зависимости от команд, формируемых УУ.

Функционирование машины Тьюринга осуществляется в соответствии с так называемой функциональной схемой (совмещённой таблицей, подоб-ной таблицам автоматов - см. подразд. 2.3.1), в каждой клетке которой записывается тройка символов: символ нового состояния и новый входной символ, а также символ команды на перемещение головки; это реакция машины на входной символ в зависимости от состояния, в котором находилась машина, т.е. (q, x) ® (q, x, u).

В табл. 2.3 приведены различные варианты реакции УУ, при которых символ в ячейке и состояние изменяются либо нет, перемещение головки имеется либо отсутствует.

Каждую строку функциональной схемы можно рассматривать как условный оператор с множеством альтернатив, определяемых значением входного символа, а имя строки (данное состояние машины) – как метку этого оператора. Тогда вся функциональная схема (ФС) представляет собой программу функционирования МТ.

Таблица 2.3

МТ	x0	...	xi	...	xn
q0	q0 x0 S	...	q0 xi S	...	q0 xn S
...	...	...	...	...	...
qj	q0 x0 L	...	qr xk S	...	qj xi R
...	...	...	...	...	...

Если функциональная схема МТ задана, то при каждом заполнении ленты работа машины однозначно определена.

Далее будем считать, что символ q₀ состояния УУ означает состояние покоя МТ, т. е. строка q₀ ФС обладает следующими свойствами:

· первым символом в каждой клетке этой строки всегда является q₀;

· вторым символом в клетке столбца x_i этой строки является символ x_i;

· третьим символом в каждой клетке строки является символ S.

Поэтому, если УУ в какой-то момент имеет состояние q₀, то где бы ни находилась головка и каким бы ни было заполнение ленты, в последуюший момент времени УУ будет оставаться в том же состоянии, заполнение ленты останется прежним, головка также не сдвинется. Для упрощения записи ФС строка q₀ в ней опускается.

В дальнейшем для простоты будем предполагать, что алфавит символов Х состоит из двух символов: "пустого" - 0 и "не пустого" - 1.

Рассмотрим несколько примеров МТ. Начальным состоянием машины здесь и далее будем считать состояние q₁; рассмотренные в этих примерах машины имеют по одному состоянию (не считая состояния покоя).

Пример 2.4. Машина А (табл. 2.4). Если в начальный момент машина воспринимает заполненную ячейку, то она "отыскивает" на ленте первую пустую (т.е. заполненную символом 0 ячейку) справа от той, над которой находится головка, вписывает туда символ 1 и останавливается. Если вначале головка находится напротив пустой ячейки, то машина её "заполняет" и останавливается, не передвигая головку.

Пример 2.5. Машина B (табл. 2.5) "стирает" единицу в той ячейке, над которой находится головка (если ячейка не пустая), передвигает головку влево и останавливается. Если в начальный момент ячейка под головкой пустая, то машина передвигает головку влево до тех пор, пока не найдёт заполненную ячейку, очищает её, передвигает головку влево и останавливается.

Пример 2.6. Машина С (табл. 2.6), отправляясь от заполненной ячейки, идёт влево и останавливается левее группы единиц на две ячейки.

Пример 2.7. Машина D (табл. 2.7), имея два состояния покоя, распознает, напротив какой ячейки находится, - пустой либо заполненной; в зависимости от этого переходит в первое либо второе состояние покоя.

В некоторых случаях МТ может быть недоопределена в том смысле, что не все ячейки её ФС заполнены. Это допускается в тех случаях, когда можно заранее сказать, что некоторые сочетания состояний машины и символов на ленте по тем или иным причинам никогда не встречаются.

Иногда МТ может иметь несколько состояний покоя: .

Таблица 2.4 Таблица 2.5 Таблица 2.6 Таблица 2.7

A

B

C

D

q1

q01S

q11R

q1

q10L

q00L

q1

q00L

q11L

q1

q0’0S

q0^’’1S

Дата добавления: 2014-01-14