Представление деревьев

Почти все машинные представления деревьев основаны на связанных распределениях, при этом каждый узел состоит из поля INFO и нескольких полей для указателей. Например, одно из представлений для каждого узла имеет единственное поле для указателя F (Father – отец) на отца данного узла. При этом приведенное на рис. 3.8 дерево будет выглядеть так, как показано на рис. 3.11.

Такое представление полез-но, если необходимо подниматься по дереву от потомков к предкам. Однако эта операция встречается довольно редко; чаще требуется спуститься по дереву от предков к потомкам.

Представление дерева (или леса) с использованием указате-лей, ведущих от предков к потомкам, довольно сложно, поскольку узел, имея не более одного отца, может иметь в то же время произвольно много сыновей. Другими словами, при таком представлении узлы должны различаться по размеру, что является определённым неудобством. Один из путей обхода этой трудности состоит в том, чтобы определить соотношение между деревьями и бинарными деревьями, поскольку бинарные деревья легко представить узлами фиксированного размера. Каждый узел в этом случае имеет три поля: LEFT (указывает положение корня левого поддерева), INFO (содержимое узла) и RIGHT (указатель местоположения корня правого поддерева). Всё сказанное выше проиллюстрировано на рис. 3.12.

Деревья можно изобразить как бинарные (используя узлы фикси-рованного размера), представляя каждый узел леса в виде узла бинарного дерева, состоящего из полей LEFT, INFO и RIGHT. При этом поле LEFT предназначается для указания самого левого сына данного узла, а поле RIGHT – для указания следующего брата этого узла.

Таким образом, поле LEFT некоторого узла используется для указателя на связанный список сыновей этого узла; этот список связывается с помощью полей RIGHT. Такое представле-ние называется естественным соответствием между лесами и бинарными деревьями.

Бинарное дерево обычно представляют в памяти машины в виде двух массивов LES (LEftSon - левый сын) и RIS (RIghtSon - правый сын). Пусть узлы бинарного дерева зануме-рованы целыми числами от 1 до N. В этом случае LES[ i ]= j тогда и только тогда, когда узел с номером j является левым сыном узла с номером i. Если у узла i нет левого сына, то LES[ i ]=0. RIS[ i ] определяется аналогично. Узел i, у которого LES[ i ] = 0, является листом. Братьями являются узлы i, j, k, для которых имеет место соотношение RIS[ i ] = j, RIS[ j ] = k.

Полное бинарное дерево высоты k часто представляют одним массивом. В позиции 1 этого массива находится корень. Левый сын узла в пози-ции i расположен в позиции 2 i, а его правый сын - в позиции [ i /2].

Рассмотрим на конкретном примере преобразование дерева (леса) в бинарное дерево, используя естественное соответствие между ними, а также приведём представление бинарного дерева в памяти ЭВМ.

Пример 3.4. Задан лес (рис. 3.13, а). Преобразуем его в бинарное дерево, для чего выстроим всех братьев в горизонтальные линии, которым будут соответствовать связанные списки братьев; при этом корни всех деревьев леса считаются также братьями. В результате такого преобразо-вания получим бинарное дерево, показанное на рис.3.13,б.

Теперь можно полученное бинарное дерево представить в виде массивов LES и RIS, сведенных в таблицу. На рис. 3.14 приведен фрагмент этой таблицы, причём в качестве индексов массивов в ней ис-пользуются имена узлов, расположенных в алфавитном порядке. Видно, что например узел С является отцом, у которого самый левый сын – узел D, а остальные сыновья (E и F) рассматриваются как следующие братья узла D. В то же время соотношение RIS[C]=G говорит о том, что узел G является братом для узла C; если теперь посмотреть на строку G, то можно увидеть ещё одного брата узлов C и G - узел H. Нули в массиве LES для строк с индексами D, E, F, G означают, что узлы с теми же именами не имеют сыновей; в строке с индексом F имеем RIS[F]=0, т.е. узел F не имеет следующего брата.

LES RIS
A	B	M	Если переименовать узлы рассматри-ваемого леса, т.е. ввести вместо букв их но-мера в алфавитном порядке, то можно убедиться, что эти номера подчиняются приведенным выше соотношениям. Так, LES[3]=4 и LES[4]=0 (C®3, D®4), т.е. узел 4 является самым левым сыном узла 3, а узел 4 не имеет сыновей.
B		C
C	D	G
D		E
E		F
F
G		H
H	I
…	…	…
Рис.3.14. Представле- ние бинарного дерева

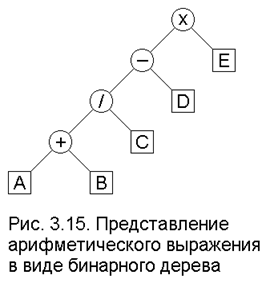
В заключение рассмотрим пример представления арифметического выражения с помощью бинарного дерева.

Пример 3.5. Арифметическое выражение с операциями +, -, ´, ¤ может быть очевидным образом представлено бинарным деревом, если в качестве операторов взять внутренние узлы, а операндами считать листья. Например, выражению ((A+B)/C - D) ´ E соответствует следующее дерево (рис. 3.15).

Дата добавления: 2014-01-14