Прохождение леса

Во многих приложениях необхо-димо пройти лес (например, в алгоритмах, построенных на деревьях, решается задача нахождения корня дерева), посещая все его узлы в определённом порядке и обрабатывая их некоторым систематическим образом.

Посещение каждого узла может быть связано с простой операцией, такой, как печать содержимого узла, или со сложной, такой, как вычисление функции. При этом предполагается, что при посещении узла структура леса не изменяется.

Представляются полезными следующие 4 основных способа прохождения леса в некотором порядке, а именно: в прямом (в глубину), обратном (снизу вверх), в горизонтальном (в ширину) и для бинарных деревьев – во внутреннем (симметричном или лексикографическом).

Прохождение в прямом порядке полезно в процедурах поиска.

Заметим, что прохождение леса в прямом порядке в точности такое же, как и прохождение в прямом порядке бинарного дерева, являющегося его представлением. Этот факт делает ²естественным² соответствие между деревом и бинарным деревом.

Обратный порядок полезен, в частности потому, что он позволяет вычислять рекурсивно определённые функции на лесах.

При горизонтальном обходе узлы леса проходятся слева направо, уровень за уровнем, от корня вниз. Такое прохождение дерева полезно в определённых алгоритмах на графах.

Рассмотрим три широко распространённых способа прохождения дерева: в прямом, обратном и внутреннем порядке.

Определение. Пусть Т - дерево с корнем r и сыновьями v₁, v_k, k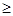 0. При k =0 это дерево состоит из единственного узла r. Тогда прохождение дерева определяется следующими рекурсиями.

В прямом порядке:

1) посетить корень r;

2) посетить в прямом порядке поддеревья с корнями v₁,..., v_k в указанной последовательности.

В обратном порядке:

1) посетить в обратном порядке поддеревья с корнями v₁,..., v_k в указанной последовательности;

2) посетить корень r;

Во внутреннем порядке:

1) посетить во внутреннем порядке левое поддерево корня (если оно существует);

2) посетить корень r;

3) посетить во внутреннем порядке правое поддерево корня (если оно существует).

Если при некотором прохождении дерева его узлам были присвоены какие-то номера, то на узлы удобно ссылаться по этим номерам. Так, v будет обозначать узел, которому был присвоен номер v. Если все узлы занумерованы в порядке посещения, то рассмотренные нумерации обладают рядом интересных свойств.

При нумерации в прямом порядке все узлы поддерева с корнем r имеют номера, не меньшие r. Точнее, если D_r - множество потомков узла r, то v будет номером некоторого узла из D_r тогда и только тогда, когда r£v < r +ïD_rï.

Поставив в соответствие каждому узлу его номер в прямом порядке и количество его потомков, легко определить, является ли некоторый узел w потомком для v, причём за фиксированное время, не зависящее от размера дерева. Номера, соответствующие обратному порядку, обладают аналогичными свойствами.

Номера узлов дерева, соответствующие внутреннему порядку, обладают таким свойством, что номера узлов в левом поддереве для v меньше v, а в правом поддереве больше v. Таким образом, чтобы найти узел с номером w, надо сравнить w с корнем r. Если w=r, то искомый узел найден. Если w<r, то надо повторить этот процесс для левого поддерева; если w>r, то повторить процесс для правого поддерева. В конце концов узел с номером w будет найден.

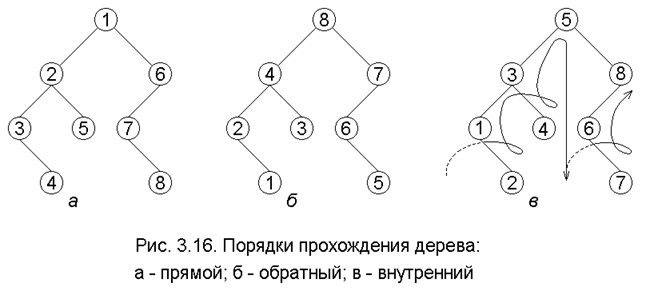Пример 3.6. На рис. 3.16 изображено двоичное дерево, узлы которого пронумерованы в соответствии с прохождением его различным образом.

Отметим, что алгоритм прохождения во внутреннем порядке подробно рассматривается в следующей главе.

Заключение

Данные, прежде чем подвергнутся обработке в машине, проходят две стадии структурирования: сначала выбираются (строятся) их матема-тические модели (математические структуры, или абстрактные типы данных по [7]), а затем они трансформируются в структуры, удобные для представления в памяти машины (машинные структуры).

Необходимость в машинных структурах данных определяется особенностью организации оперативной памяти (ОП) – доступ к ячейкам памяти является произвольным, а ячейки нумеруются подряд. Поэтому естественным является расположение в ОП подряд некоторой совокуп-ности данных – это последовательное распределение, характерное для статических структур данных. Если же нужно изменять количество данных в совокупности, то удобнее данные в ОП располагать произвольно, но они должны быть связаны в совокупность с помощью указателей на следу-ющее данное – это связанное распределение, характерное для динами-ческих структур данных.

В соответствии с формулой Н. Вирта [6] для построения эффек-тивного алгоритма требуется выбрать подходящие структуры данных; этот выбор определяется операциями, которые будут проводиться над данными.

Для представления множеств, графов и деревьев в машине могут быть использованы различные структуры данных; чаще всего это списки.

Списки могут иметь сложную структуру. Так, в списке каждая ком-понента может также являться списком. Возможно иерархическое постро-ение структур данных, например, в виде дерева стеков.

Время выполнения операций над списком не зависит от его длины.

Обход деревьев применяют в комбинаторных задачах; наиболее часто используются 3 способа обхода: прямой, обратный и внутренний.

Контрольные вопросы. Упражнения

1. Какую структуру данных целесообразно использовать при составлении алгоритма решения задачи поиска пути в лабиринте?

2. Какую структуру данных целесообразно использовать при составлении алгоритма решения задачи «Ханойские башни»?

3. Что общего у стека и очереди, в чём их различие?

4. Почему время выполнения операции вставки элементов в список любого вида либо удаления из него не зависит от длины списка?

5. Напишите на псевдоязыке программу печати элементов односвязного списка, используя операцию readel (чтение элемента списка без его удаления) и вспомогательный регистр RG.

6. Напишите процедуру обмена элементами в позициях p и NEXT[ p ] для односвязного списка.

7. Напишите на псевдоязыке программы вставки, удаления и обмена элементов последовательности ключей при их сортировке методом простого выбора, используя список для готовой подпоследовательности и массив – для входной подпоследовательности.

8. В условиях предыдущего упражнения используйте стек и очередь.

9. Рассмотрим многочлен вида 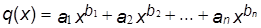, где b₁ > b₂ >…> b_n ³0. Такой многочлен можно представить в виде связанного списка, где каждая ячейка имеет три поля: одно – для коэффициента a_i; второе - для показателя степени b_i; третье – для указателя на следующую ячейку. Для описанного представления многочленов напишите программы их сложения, умножения, дифференцирования и интегрирования.

10. Как реализовать очередь, если её элементами являются символьные строки произвольной длины? Сколько времени необходимо для операции вставки элемента в очередь?

Дата добавления: 2014-01-14