Асимптотика

Комбинаторные вычисления на конечных множествах

4.1.1. Введение в комбинаторику

Предметом теории комбинаторных алгоритмов, часто называемой комбинаторными вычислениями, являются вычисления на дискретных математических структурах. В этой теории большое внимание уделяется алгоритмическому подходу к решению задач дискретной математики, оптимизации перебора вариантов, сокращению числа рассматриваемых решений.

Область комбинаторных алгоритмов включает в себя задачи, которые требуют подсчёта (оценивания) числа элементов в конечном множестве или перечисления этих элементов в специальном порядке (приложение Б). При этом широко применяется процедура выбора элементов с возвращением и её варианты.

Существуют два вида задач подсчёта. В простом случае задаётся конкретное множество и требуется определить точно число элементов в нём. В общем случае имеется семейство множеств, заданное некоторым параметром, и определяется мощность множества как функция параметра. При этом часто бывает достаточной оценка порядка функции, а иногда требуется только оценка скорости её роста. Например, если мощность подлежащего рассмотрению множества растёт по некоторому параметру экспоненциально, то этого может оказаться достаточно для того, чтобы отказаться от предложенного подхода к изучению проблемы, не занимаясь различными деталями. К этому, более общему, типу проблем применяются процедуры асимптотических разложений, рекуррентных соотношений и производящих функций.

Асимптота — особая линия (чаще всего прямая), являющаяся предельной для рассматриваемой кривой.

Асимптотика — это искусство оценивания и сравнения скоростей роста функций. Говорят, что при х ®¥ функция 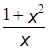"ведёт себя, как х ", или "возрастает с такой же скоростью, как х ", и при х ®0 "ведёт себя, как 1/ x ". Говорят, что "log x при x ®0 и любом e>0 ведёт себя, как x ^e, и что 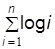при n ®¥ растёт не быстрее, чем n log n ". Такие неточные, но интуитивно ясные утверждения полезны при сравнении функций так же, как и соотношения <, £ и = при сравнивании чисел.

Определим три основных асимптотических соотношения.

Определение 1. Функция f (x) эквивалентна g (x) при х ® x₀, если и только если 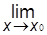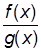=1.

В этом случае говорят, что функция f (x) асимптотически равна функции g (x) или что f (x) растёт с такой же скоростью, как и g (x).

Определение 2. f (x)=o(g (x)) при x ® x₀, если и только если 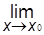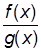=0.

Говорят, что при x ® x₀ f (x) растёт медленнее, чем g (x), или что f (x) "есть о-малое" от g (x).

Определение 3. f (x)=О(g (x)) при x ® x₀, если и только если существует константа С такая, что sup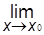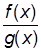=С.

В этом случае говорят, что f (x) растёт не быстрее, чем g (x), или что при x ® x₀ f (x) "есть О-большое" от g (x).

Cоотношение f (x)= g (x)+ o (h (x)) при x ®¥ означает, что f (x)-g (x) =o (h (x)). Аналогично f (x)= g (x)+ О (h (x)) означает, что f (x) -g (x) =О (h (x)).

Выражения О(·) и о(·) могут использоваться также и в неравенствах. Например, неравенство x + o (x)£2 x при x ®0 означает, что для любой функции f (x) такой, что f (x) =o (x), при x ®¥ имеет место соотношение x+f (x)£2 x для всех достаточно больших значений х.

Приведём некоторые полезные асимптотические равенства.

Полином асимптотически равен своему старшему члену:

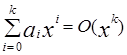при x ®¥; (4.1)

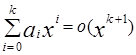при x ®¥; (4.2)

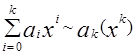при x ®¥ и a_k ¹0. (4.3)

Суммы степеней целых чисел удовлетворяют соотношению:

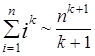при n ®¥. (4.4)

Отсюда, в частности, имеем при n ®¥

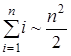и 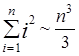. (4.5)

В более общем случае при n ®¥ и для любого целого k ³0

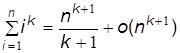; (4.6)

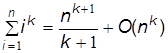. (4.7)

Дата добавления: 2014-01-14