Производящие функции

При работе с последовательностями используется идея: каждой числовой последовательности сопоставляется некоторая функция действительного (комплексного) переменного таким образом, чтобы обычным операциям над последовательностями соответствовали простые операции над сопоставленными функциями. Наиболее общим в комбинаторике является сопоставление последовательности x₀, x₁, x₂,… производящей функции X(s) = действительной переменной s.

Проиллюстрируем использование полиномиальных производящих функций для вывода нескольких важных формул для сочетаний без повторений на примере бинома Ньютона

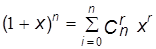. (4.17)

Рассмотрим следующие частные случаи:

а) если x = 1, то 2 ⁿ =; это выражение позволяет определить количество подмножеств некоторого множества;

б) если x = -1, то 0 =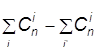, т.е. ,

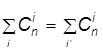где i - чётное, а i’ – нечётное.

Для сочетаний с повторениями используется полиномиальная производящая функция X(s)=1 + s₁x + s₂x² +…, коэффициенты s_r которой представляют собой r -сочетания из n различных элементов с повторениями. Эта функция является обобщением бинома Ньютона, которая рассматривается как произведение многочленов разных степеней, причём старшая степень каждого из перемножаемых многочленов задаётся специфи-кацией (приложение Б). Например, для r -сочетаний из трёх элементов a, b, c со спецификацией {3, 1, 2} имеем

(1 + x + x ² + x ³)(1 + x)(1 + x + x ²)=1 + 3 x + 5 x ² + 6 x ³ + 5 x ⁴ + 3 x ⁵ + x ⁶.

Здесь коэффициент при x^r дает искомое число r -сочетаний. Так, имеется пять 2-сочетаний (аа, ab, ac, bc, cc), шесть 3-сочетаний (aaa, aab, aac, abc, acc, bcc) и т. д.

Дата добавления: 2014-01-14