Метод Ньютона решения систем нелинейных уравнений

Пусть дана система нелинейных уравнений.

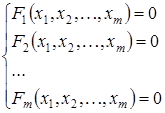(3.5)

Идея метода Ньютона заключается в том, что в окрестности имеющегося приближения к решению системы (3.5) задача заменяется некоторой вспомогательной линейной задачей.

В основе метода Ньютона для системы уравнений (3.5) лежит использование разложения функций 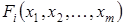в ряд Тейлора, причем члены, содержащие производные второго и более высоких порядков, отбрасывают.

Пусть приближенные значения неизвестных системы (3.5) (например, полученные в результате предыдущей итерации) равны соответственно 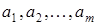. Задача состоит в нахождении приращений (поправок) к этим значениям 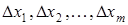, благодаря которым решение системы (3.5) запишется в виде:

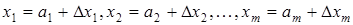(3.6)

Проведем разложение левых частей уравнений (3.5) с учетом (3.6) в ряд Тейлора, ограничиваясь лишь линейными членами относительно приращений:

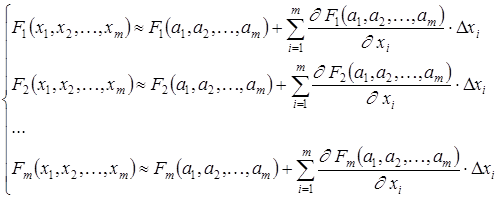
Поскольку в соответствии с (3.5) левые части этих выражений должны обращаться в нуль, то приравниваем к нулю и правые части. Получим следующую систему линейных алгебраических уравнений относительно приращений .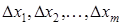

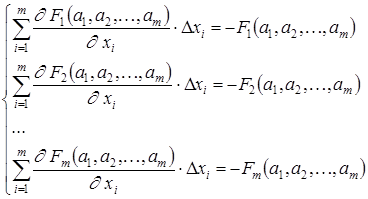(3.7)

Определителем системы (3.7) является якобиан

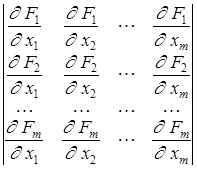
(Производные вычислены в точке 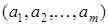). Для существования и единственности решения системы (3.7) он должен быть отличен от нуля (на каждой итерации).

Таким образом, итерационный процесс решения системы уравнений (3.5) методом Ньютона состоит в определении приращений 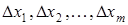к значениям неизвестных на каждой итерации. Процесс прекращается, если все приращения становятся малыми по абсолютной величин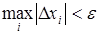е: , где – заданная точность. При определенных условиях, наложенных на функции 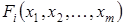, и при удачном выборе начального приближения каждый шаг итерационного процесса выполним и последовательность итераций сходится к решению системы (3.5), причем этот метод имеет второй порядок сходимости.

Глава 4.

Дата добавления: 2014-01-14