Корректирующие свойства групповых кодов

ДРУГИЕ СВОЙСТВА ГРУППОВЫХ КОДОВ

Задачи

1. Определить минимальное кодовое расстояние в коде, состоящем из следующих кодовых комбинаций: 000, 001, 110, 111.

2. Построить (3, 2) – код с d_min =2.

3. Можно ли построить групповой код длины n=3 с dmin= 3? Если да, то какой это код?

4. Задана проверочная матрица (7, 4) – кода:

Построить порождающую матрицу для этого кода.

5. Проверить, принадлежит ли комбинация 1 0 1 0 1 0 1 коду (7, 4) предыдущей задачи.

6. Для кода, двойственного коду(5,3), написать порождающую и проверочную матрицы в канонической форме.

Эффективность помехоустойчивого кода определяется минимальным кодовым расстоянием. Выше было показано, что d_min (n,k)- кода равно минимальному весу ненулевых кодовых комбинаций. Желательно уметь вычислять d_min кода, не находя весов всех кодовых комбинаций. Для групповых кодов существует способ определения d_min по виду матрицы проверок . Этот способ основывается на соотношении .

Пусть V - кодовая комбинация с минимальным весом.

Умножение кодовой комбинации V на матрицу 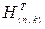можно представить как поразрядное сложение столбцов матрицы , которым соответствуют единицы комбинации v.

Результат умножения должен дать нулевой синдром. Так как никакая другая комбинация с меньшим числом единиц не дает нулевого синдрома, то, следовательно, кодовой комбинации минимального веса соответствует минимальное число линейно зависимых столбцов матрицы проверок. Таким образом, можно сформулировать правило определения d_min группового кода.

Теорема 5.1.

Групповой код имеет минимальный вес (минимальное кодовое расстояние), равное минимальному числу линейно зависимых столбцов матрицы проверок .

Пример 5.9. Код (5, 3) имеет d_min =2, так как в его состав входят комбинации (10 100) и (01 001). Рассмотрим умножение этих комбинаций на матрицу :

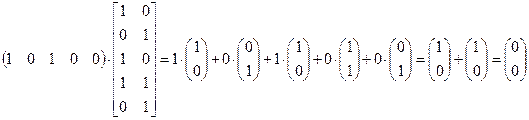
То есть комбинации (10100) соответствует линейная зависимость 1-го и 3-го столбцов . Аналогично проверяется, что комбинации (01001) соответствует линейная зависимость 2-го и 5-го столбцов.

Дата добавления: 2014-01-14