Б. Процедура декодирования

А. Процедура кодирования

Процедуры кодирования и декодирование группового кода

1.Процедура кодирования на основе порождающей матрицы

Пусть требуется получить кодовую комбинацию (n,k)-кода V_i, соответствующую некоторому сообщению источника информации, представленному в виде безызбыточной k -элементной последовательности k_{i .} Как было показано выше, эта задача решается составлением линейной комбинации строк порождающей матрицы:

V_i=k_i1V₁+k_i2V₂+…+ k_ikV_k, где Vj, j=1 … k,-кодовые комбинации (n,k)-кода, являющиеся строками канонической формы порождающей матрицы этого кода, k_i,j - элементы кодируемой k - элементной последовательности.

Указанная линейная комбинация соответствует умножению последовательности k_i на порождающую матрицу кода, представленную в канонической форме:

k_i ×G_(n,k)=k_{i ×} [RI_k]=(k_iR,k_i)

В результате умножения получим n- элементную кодовую комбинацию V_i, у которой на местах избыточных элементов (v_1,v_2,…v_n-k) находятся последовательность r_i=k_iR, а на местах информационных элементов- (v_n-k+1,…,v_n)- исходная кодируемая последовательность k_i.

2_. Процедура кодирования на основе проверочной матрицы.

В этом случае процедура кодирования основана на известном уравнении.

V_i×H^T_(n,r)=0.

Представим V_i в виде (r_i,k_i), где r_i - последовательность избыточных элементов кодовой комбинации, а k_i - последовательность информационных элементов. Представляя H^T_(n,k) в канонической форме, получаем: (r_i,k_i)×[I_n-kR^T ]^T=r_i+k_iR=0, откуда r_i=k_iR..

Из полученного решения видно, что избыточные элементы в точности совпадают с избыточными элементами при кодировании на основе G_(n,k)

В тех случаях, когда (n-k)<k или ^k ∕ n > ¹∕2, кодирование на основе проверочной матрицы H(_n,k) требует меньшего количества вычислений.

Пусть - кодовые комбинации некоторого группового кода, где - нулевая комбинация, то есть единичный элемент группы. Процедура декодирования для этого кода может быть выработана на основе следующих построений. Строится таблица декодирования как таблица разложения группы всевозможных n – элементных двоичных комбинаций на смежные классы по подгруппе, составляющей данный код. Образующие смежных классов выбираются таким образом, чтобы в их состав вошли все наиболее вероятные для используемого канала связи образцы ошибок в кодовой комбинации. Для большей части реальных каналов связи в качестве образующих смежных классов следует выбирать комбинации с минимальным весом в данном смежном классе.

Выпишем в качестве первой строки таблицы все кодовые комбинации, начиная с нулевой. В качестве образующих смежных классов возьмем наиболее вероятных образцов ошибок для используемого канала (e_i).

2 ^k столбцов

2 ^n-k строк

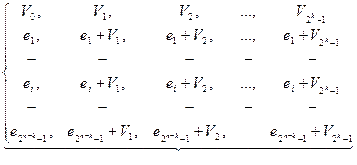
Каждый из столбцов таблицы декодирования является защитной зоной для кодовой комбинации, стоящей во главе столбца.

Решение о наличии ошибок в кодовой комбинации и их структуре производится по виду синдрома

.

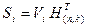Покажем, что каждому образцу исправляемой ошибки соответствует вполне определенный синдром.

Если синдром чисто нулевой, то считается, что ошибки в кодовой комбинации отсутствуют, хотя это и не всегда верно, так как комбинациям с необнаруженными ошибками также соответствует нулевой синдром.

Предположим, что кодовая комбинация принята с исправляемой ошибкой, то есть

,

где 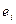- образец ошибки, являющейся образующим смежного класса.

В этом случае синдром принимает вид:

,

то есть для каждого образца исправляемых ошибок или, что тоже самое,

для каждого смежного класса существует свой синдром.

Переданная комбинация будет декодирована, верно по принятой комбинации 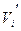тогда и только тогда, когда вектор ошибки 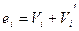является образующим смежного класса, которому принадлежит .

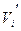Процесс декодирования при использовании таблицы декодирования для исправления ошибок заключается в следующем:

1. Для принятой комбинации вычисляется синдром и определяется смежный класс, которому принадлежит принятая комбинация.

2. Определяется образующий смежного класса, которому принадлежит принятая комбинация, являющийся предполагаемой ошибкой.

3. Суммируя по модулю 2 предполагаемый образец ошибки с принятой комбинацией, получаем переданную комбинацию.

Таким образом, при исправлении ошибок в кодовой комбинации указанным методом количество исправляемых ошибок не может превышать числа смежных классов, то есть числа , и в точности равно этому числу в тех случаях, когда в каждом смежном классе имеется единственная комбинация, соответствующая наиболее вероятной структуре ошибок

Коды, которые исправляют все ошибки кратности до t включительно и не исправляют никаких ошибок большей кратности, называются совершенными.

При обнаружении ошибок процедура декодирования упрощается. Если вычисленный синдром , то выдается сигнал “ошибка” или ”стирание”.

При этом сам вид синдрома не имеет значения, т.е. все смежные классы объединяются в общую защитную зону. При частичном исправлении и обнаружении ошибок задается кратность ошибок , до которой осуществляется исправление, а ошибки высших кратностей только обнаруживаются, поэтому в таблице декодирования выделяется 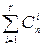образцов ошибок, подлежащих исправлению. Все же остальные смежных классов объединяются в общую защитную зону. Если синдром, соответствующий принятой комбинации принадлежит общей защитной зоне, то фиксируется обнаружение ошибки – “стирание”.

Если синдром принадлежит смежному классу с исправляемым образом ошибки, то происходит исправление ошибки, как это было описано выше.

Пример 5.10. Рассмотрим таблицу декодирования для (5, 3) – кода, используемого в предыдущих примерах.

	(5, 3) код (подгруппа) 10100 11010 01001 01110 11101 10011 00111
	10101 11011 01000 01111 11100 10010 00110
	10110 11000 01011 01100 11111 10001 00101
	10000 11110 01101 01010 11001 10111 00011

Из анализа таблицы декодирования можно сделать следующие выводы:

1. Синдромы имеют значения

,

,

,

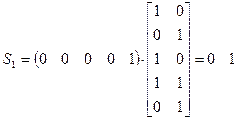т.е. все синдромы разные и вид синдрома однозначно указывает смежный класс.

2. Код исправляет не все образцы одиночных ошибок. Например, комбинации 0 0 0 0 1 и 0 1 0 0 0, также как и 0 0 1 0 0 и 1 0 0 0 0 принадлежат одному смежному классу, следовательно, обе пары этих образцов ошибок не могут быть исправлены. Это понятно, так как d_min этого кода равно 2, а для исправления всех вариантов одиночных ошибок необходимо иметь d_min =3.

Действительно, мы находим в смежном классе с образующим 0 0 0 0 1 еще одну комбинацию веса 1 – 0 1 0 0 0, т.е. синдрому S₁ = 0 1 соответствует два равновероятных образца однократных ошибок; синдрому S₂ = 1 0 также соответствуют два образца равновероятных однократных ошибок. Только лишь синдрому S₃ = 1 1 соответствует единственный образец однократной ошибки 0 0 0 1 0.

Таким образом, однозначно исправляются только лишь комбинации, принадлежащие одному смежному классу, т.е. ошибка вида 0 0 0 1 0 данным кодом исправляется.

Дата добавления: 2014-01-14