
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Способ выделения сигнала фазового запуска по зачетному отрезку
|
|
|
|
При данном способе от передатчика передается 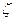 -элементная комбинация фазового запуска
-элементная комбинация фазового запуска 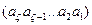 . В отличие от ранее рассмотренного способа на приеме в каждый момент времени анализируется только
. В отличие от ранее рассмотренного способа на приеме в каждый момент времени анализируется только  элементов
элементов 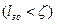 . Последовательность из
. Последовательность из  элементов называют зачетным отрезком, так как выделение сигнала фазового запуска производится при совпадении принятой
элементов называют зачетным отрезком, так как выделение сигнала фазового запуска производится при совпадении принятой  -элементной последовательности с аналогичной последовательностью комбинации фазового запуска, содержащейся в памяти приемного устройства или получаемой в нем по заданному правилу. Моменты выделения фазового запуска должны соответствовать концу КФЗ, т.е. моменту приема элемента
-элементной последовательности с аналогичной последовательностью комбинации фазового запуска, содержащейся в памяти приемного устройства или получаемой в нем по заданному правилу. Моменты выделения фазового запуска должны соответствовать концу КФЗ, т.е. моменту приема элемента 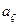 , поэтому все
, поэтому все 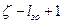 зачетных отрезков, которые могут быть получены из КФЗ, должны быть различны и однозначно связаны с их местом в КФЗ.
зачетных отрезков, которые могут быть получены из КФЗ, должны быть различны и однозначно связаны с их местом в КФЗ.
На рис. 10.5а показана структурная схема устройства выделения сигнала фазового запуска по зачетному отрезку. Принимаемая последовательность поступает во входной регистр и после приема очередного элемента  -элементный зачетный отрезок передается в сравнивающее устройство. В этом устройстве он сравнивается со всеми отрезками КФЗ. Если не произойдет сравнения, то берется следующий зачетный отрезок, получаемый после приема очередного элемента. Если зачетный отрезок совпадает с одним из отрезков КФЗ, то в устройство определения момента выделения сигнала фазового запуска, в зависимости от вида совпавшего отрезка, в соответствующий момент выделяется сигнал фазового запуска.
-элементный зачетный отрезок передается в сравнивающее устройство. В этом устройстве он сравнивается со всеми отрезками КФЗ. Если не произойдет сравнения, то берется следующий зачетный отрезок, получаемый после приема очередного элемента. Если зачетный отрезок совпадает с одним из отрезков КФЗ, то в устройство определения момента выделения сигнала фазового запуска, в зависимости от вида совпавшего отрезка, в соответствующий момент выделяется сигнал фазового запуска.
При реализации способа выделения сигнала фазового запуска по зачетному отрезку наиболее часто в качестве КФЗ используется последовательность, получаемая с помощью регистров

Рис. 10.5
с обратными связями. На рис. 10.5б показан такой регистр, построенный по полиному

и применяемый в качестве устройства формирования комбинации фазового запуска.
С помощью подобных регистров можно получить последовательности с периодом Т, равным показателю бинома наименьшей степени 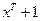 , в разложение которого входит полином h(x). Максимальный период
, в разложение которого входит полином h(x). Максимальный период 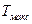 , равный
, равный 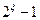 , будет в случае, если полином h(x) примитивный, т.е. если он не входит в разложение никакого бинома степени, меньшей
, будет в случае, если полином h(x) примитивный, т.е. если он не входит в разложение никакого бинома степени, меньшей 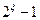 . Для упрощения реализации берут полиномы веса 3. Например, можно указать следующие примитивные полиномы веса 3:
. Для упрощения реализации берут полиномы веса 3. Например, можно указать следующие примитивные полиномы веса 3:
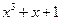 ;
; ;
;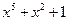 ;
;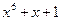 ;
;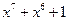 ;
;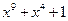 ;
;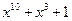 ;
; .
.
На рис. 10.6 показана функциональная схема устройства фазирования по циклу, использующего способ выделения сигнала фазового запуска по зачетному отрезку.
В передатчике аппаратуры передачи дискретной информации имеется регистр с обратными связями, построенный по многочлену  и осуществляющий формирование комбинации фазового запуска. В приемнике АПД в составе устройства выделения сигнала фазового запуска имеется такой же регистр, но в начале процесса формирования обратная связь этого регистра разомкнута с помощью схемы
и осуществляющий формирование комбинации фазового запуска. В приемнике АПД в составе устройства выделения сигнала фазового запуска имеется такой же регистр, но в начале процесса формирования обратная связь этого регистра разомкнута с помощью схемы 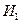 . Выход регистра передатчика через открытую схему «Запрет» подключен к цепи обратной связи приемника.
. Выход регистра передатчика через открытую схему «Запрет» подключен к цепи обратной связи приемника.
Процесс фазирования начинается с записи «1» в ячейку 1 передающего регистра (табл. 10.3). Регистр приемника находится при этом в состоянии 000. На следующем такте оба регистра перейдут в одинаковое состояние 100. Начиная с этого момента на вход счетчика  нулей будут подаваться нули. Это происходит потому, что последовательности, получаемые на выходах приемного и передающего регистра, совпадают. После того, как счетчик
нулей будут подаваться нули. Это происходит потому, что последовательности, получаемые на выходах приемного и передающего регистра, совпадают. После того, как счетчик  нулей отсчитает четыре нуля, на его выходах появляются сигналы, с помощью которых закрывается схема «Запрет» и открываются схемы
нулей отсчитает четыре нуля, на его выходах появляются сигналы, с помощью которых закрывается схема «Запрет» и открываются схемы 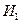 и
и 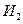 . Следовательно, приемный регистр начинает работать в режиме генерации последовательности, полностью совпадающей с последовательностью, генерируемой передающим регистром. Так как выход канала закрыт схемой «Запрет», то ошибки в канале не могут повлиять на последовательность, генерируемую приемным регистром. Момент фазового запуска определяется дешифратором комбинации 100. Появление этой комбинации вызывает синфазный запуск приемного распределителя по отношению к передающему.
. Следовательно, приемный регистр начинает работать в режиме генерации последовательности, полностью совпадающей с последовательностью, генерируемой передающим регистром. Так как выход канала закрыт схемой «Запрет», то ошибки в канале не могут повлиять на последовательность, генерируемую приемным регистром. Момент фазового запуска определяется дешифратором комбинации 100. Появление этой комбинации вызывает синфазный запуск приемного распределителя по отношению к передающему.
Выбор величин 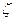 и
и  определяется требованиями к вероятностям преждевременного запуска
определяется требованиями к вероятностям преждевременного запуска  и незапуска
и незапуска  .
.
Вероятность  уменьшается с ростом
уменьшается с ростом  , а вероятность
, а вероятность  увеличивается. Увеличением
увеличивается. Увеличением 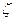 можно уменьшить вероятность
можно уменьшить вероятность  . Окончательный выбор величин
. Окончательный выбор величин 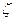 и
и  может быть проведен лишь при учете конкретных требований к вероятностям
может быть проведен лишь при учете конкретных требований к вероятностям  и
и  и структуры ошибок в дискретном канале связи.
и структуры ошибок в дискретном канале связи.
Способ выделения сигнала фазового запуска с помощью зачетных отрезков позволяет при простой реализации применить длинные комбинации фазового запуска. На практике широко применяется комбинация длины 512, полученная при помощи регистра, обратные связи которого соответствуют многочлену 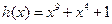 .
.

Рис. 10.6
Табл. 10.3

Алфавитный указатель терминов.
Стр.
Алгоритм Форни………………………………………………………………………………98
Векторное пространство……………………………………………………………………...16
Генератор элементов поля GF(2)…………………………………………………………..102
Граница Варшамова-Гилберта………………………………………………………………...10
Граница Синглтона…………………………………………………………………………….10
Граница Хэмминга……………………………………………………………………………..10
Группа…………………………………………………………………………………………..12
Группа циклическая…………………………………………………………………………..68
Защитная область кода………………………………………………………………………...2
Защитная область кодовой комбинации……………………………………………………..2
Идеал…………………………………………………………………………………………..60
Избыточность кода…………………………………………………………………………….6
Избыточный символ…………………………………………………………………………...6
Линейные переключательные схемы………………………………………………………103
Многочлен значений ошибок………………………………………………………………...95
Многочлен локаторов ошибок……………………………………………………………….95
Многочлен синдромный……………………………………………………………………...95
Ключевое уравнение для циклических кодов……………………………………………….95
Код Боуза-Чоудхури-Хоквингема…………………………………………………………....80
Код двойственный…………………………………………………………………………….22
Код групповой………………………………………………………………………………...16
Код с единственной проверкой на чётность………………………………………………...43
Код неразделимый……………………………………………………………………………...4
Код помехоустойчивый………………………………………………………………………..2
Код разделимый………………………………………………………………………………..4
Коды Рида-Соломона…………………………………………………………………………88
Код циклический……………………………………………………………………………...71
Код эквивалентный…………………………………………………………………………...21
Кодовое расстояние……………………………………………………….…………………...4
Кодовое расстояние минимальное…………………………………………………………....4
Кодовая комбинация запрещённая…………………………………………………………....2
Кодовая комбинация разрешённая………………………………………….………………..2
Кольцо………………………………………………………………………………………....60
Кольцо класса вычетов…………………………………………………………………….…61
Кольцо многочленов по модулю f(x)………………………………………………………..62
Конечное поле………………………………………………………………………………..64
Кратность гарантийно исправляемых ошибок……………………..……………………….5
Кратность гарантийно исправляемых ошибок………………………………………………5
Проверочные векторы……………………………………………………..…………………22
Проверочная матрица кода………………………………………………….……………….22
Проверочный многочлен…………………………………………………………………….73
Поле примитивное……………………………………………………………………………69
Поле простое……………………………………………………………………………….....64
Поле расширенное……………………………………………………………………………64
Порождающая матрица группового кода…………………………………………………...20
Порождающая матрица группового кода, каноническая форма…………………………..20
Порождающий многочлен для (n, n-1)-кодов………………………………………………82
Порождающий многочлен для общего случая циклического кода……………………….82
Порядок поля………………………………………………………………………………....64
Порядок элемента………………………………………………………………………….....68
Проверочные векторы………………………………………………………………………..22
Процедура декодирования для групповых кодов……………………………………….28,29
Процедура декодирования для циклических кодов……………………………………….101
Процедура кодирования для групповых кодов……………………………………………..28
Процедура кодирования для циклических кодов………………………………………….100
Процедура Ченя……………………………………………………………………………….96
РС-коды расширенные……………………………………………………………………….91
РС-коды укороченные………………………………………………………………………..92
Синдром……………………………………………………………………………….............22
Схема Горнера………………………………………………………………………………...96
Сумматор……………………………………………………………………………………..103
Умножитель………………………………………………………………………………….103
Элемент единичной задержки………………………………………………………………103
Содержание
ТЕМА 1. Основные понятия и определения в области ПДС…………………………………..…...1
1.1.Дискретность……………………………………………………………………………………….1
1.2.Модуляция………………………………………………………………………………………….2
1.3.Кодирование………………………………………………………………………………………..4
1.4.Упрощенная структурная схема аппаратуры ПДС………………………………………………5
1.5. Основные параметры и характеристики системы ПДС………………………………………...9
ТЕМА 2. Системные характеристики систем передачи дискретных сообщений………………..10
2.1 Понятие об эталонной модели взаимодействия открытых систем…………………………....10
2.2. Понятие о телеуслугах…………………………………………………………………………...13
2.3 Первичные коды в системах ПДС…………………………………………………………….…15
2.3.1. Телеграфные коды……………………………………………………………………..15
2.3.2. Коды для передачи данных……………………………………………………………16
ТЕМА 3. Основные характеристики физического уровня…………………………………………21
3. 1. Понятия об искажениях дискретных сигналов………………………………………………..21
3.1.1 Классификация искажений……………………………………………………………..23
3.1.2. Характеристические краевые искажения……………………………………………..23
3.1.3. Краевые искажения типа преобладаний……………………………………………...24
3.1.4. Случайные искажения…………………………………………………………………26
3.2 Понятие о методах регистрации дискретных сигналов………………………………………...27
3.2.1. Метод стробирования………………………………………………………………….27
3. 2. 2. Интегральный метод…………………………………………………………………..29
3.3. Оценка эффективности методов регистрации………………………………………………… 31
3.3.1. Распределение краевых искажений……………………………………………………31
3.3.2 Распределение дроблений………………………………………………………………33
3.3.3 Расчет вероятности ошибки при краевых искажениях……………………………….35
3.3.4 Расчет вероятности ошибки при дроблениях………………………………………….35
3.4 Модели дискретных каналов……………………………………………………………………..36
3.4.1 Поток ошибок в дискретном канале……………………………………………………36
3.4.2 Методы выявления и исследования последовательностей ошибок………………….38
3.4.3 Основные закономерности распределения ошибок в реальных каналах связи……..39
3.4.4 Математические модели дискретных каналов с группированием ошибок.………………...44
ТЕМА 4. Устройство синхронизации по элементам (УСП)……………………………………….47
4.1.Назначение и классификация……………………………………………………………………47
4.2. Обоснование необходимости устройства синхронизации но элементам. Расчет вероятности удержания синхронизма……………………………………………………………………………………….48
4.3.Схема ФАПЧ с дискретным управлением………………………………………………………49
4.4.Основные характеристики системы ФАПЧ……………………………………………………..50
4.5.Модели последовательностей ошибок в дискретном канале………………………………….50
ТЕМА 5. ЛИНЕЙНЫЕ (n,k)-КОДЫ…………………………………………………………………..51
5.1 Определение помехоустойчивых кодов и их общие характеристики…………………………..51
5.1.1Принципы построения помехоустойчивых кодов………………………………………..51
5.1.2Основные характеристики помехоустойчивых кодов……………………………………56
5.1.3Классификация помехоустойчивых кодов………………………………………………..59
5.1.4Граничные соотношения между характеристиками помехоустойчивых кодов………..60
5.1.5.Задачи……………………………………………………………………………………….61
5.2. Групповые коды и способы их описания………………………………………………………...62
5.2.1 Основные алгебраические системы, используемые в теории кодирования……………62
5.2.2Способы представления кодовых комбинаций…………………………………………...68
5.2.3Определение группового кода……………………………………………………………..69
5.2.4 Матричное описание групповых кодов…………………………………………………...70
5.2.5. Задачи ……………………………………………………………………………………...79
5.3. Другие свойства групповых кодов……………………………………………………………….80
5.3.1 Корректирующие свойства групповых кодов………………………………………….80
5.3.2 Процедуры кодирования и декодирование группового кода………………………….81
5.3.3 Укорочение кода………………………………………………………………………….85
5.3.4 Оценка эффективности групповых кодов……………………………………………….85
5.3.5 Смежно-групповые коды…………………………………………………………………89
5.3.6 Задачи………………………………………………………………………………………..90
5.4 Примеры групповых кодов………………………………………………………..………………91
5.4.1. Коды с единственной проверкой на четность……………………………………………91
5.4.2. Коды Хэмминга…………………………………………………………………………….92
5.4.3 Итеративные коды…………………………………………………………………………..98
5.4.4 Задачи………………………………………………………………………………………101
ТЕМА 6. ДВОИЧНЫЕ ЦИКЛИЧЕСКИЕ (n,k) – КОДЫ………………………………………… 102
6.1 Основные алгебраические системы, используемые в теории кодирования…………………102
6.2. Определение циклического кода……………………………………………………………... 113
6.3. Построение порождающей и проверочной матриц циклических кодов…………………….115
6.4. Коды Боуза-Чоудхури-Хоквингема (БЧХ)……………………………………………………122
6.5. Выбор порождающего многочлена для кода БЧХ……………………………………………124
6.6. Эффективность двоичных кодов БЧХ………………………………………………………….128
6.7 Кодирующие и декодирующие устройства циклических кодов……………………………...130
6.7.1 Процедура кодирования и декодирования для циклических кодов…………………...130
6.7.2. Линейные переключательные схемы, используемые в кодирующих и декодирующих устройствах циклических кодов……………………………………………………………………………..135
6.7.3. Схемы кодирующих устройств циклических кодов…………………………………...145
6.7.4. Декодирующие устройства циклических кодов……………………………………...150
ТЕМА 7. КОДЫ РИДА СОЛОМОНА (РС)………………………………………………………..159
7.1. Задачи…………………………………………………………………………………………...169
7.2. Быстрое декодирование кодов БЧХ…………………………………………………………..170
7.3. Задачи…………………………………………………………………………………………...179
ТЕМА 9. НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ КЛАССЫ КОДОВ. СОСТАВНЫЕ КОДЫ.181
9.1. Коды для исправления пачек ошибок…………………………………………………………181
9.2. Коды на основе последовательностей максимальной длины………………………………..184
9.3. Коды для асимметричных каналов…………………………………………………………….185
9.4 Каскадные коды………………………………………………………………………………….187
ТЕМА10. Цикловая синхронизация193
10.1Назначение и классификация способов цикловой синхронизации…………………………193
10.2.Способ установки фазы приемного распределителя путем сдвига………………………...195
10.3.Способ мгновенной установки фазы по комбинации фазового запуска…………………..198
10.4. Маркерный способ выделения сигнала фазового запуска…………………………………199
10. 5. Способ выделения сигнала фазового запуска по зачетному отрезку…………………….202
Приложение 1 Коды БЧХ…………………………………………………………………..................................
Приложение 2 Таблица сложения в поле GF(24)……………………………………………………………….
Приложение 3 Таблица сложения в поле GF(25)……………………………………………………………….
Алфавитный указатель…………………………………………………………………………………
Список литературы…………………………………………………………………………..................
ПРИЛОЖЕНИЕ
Коды БЧХ
| n | K | dmin | g(x) | ||
| cомножители Fi(x) | cтепени Fi(x) | корни (j) | |||
| 29(31) | |||||
| 93(95) | |||||
| 109(111) | |||||
| 117(119) | |||||
| 125(127) | |||||
1. В таблице приведены параметры кодов БЧХ с длиной кодовой комбинации n =2l–1. Для каждого (n, k)-кода указаны d min – минимальное кодовое расстояние, сомножители порождающего многочлена, их степени и корни этих сомножителей. В круглых скобках приведены уточненные значения d min.
2. Сомножители fi (x) порождающего многочлена g (x) представлены в восьмеричной форме, причем степени fi (x) убывают слева направо.
Например, восьмеричное представление 103 соответствует двоичному 001000011, а им соответствует многочлен fi (x)= x 6+ x +1.
3. Для нахождения порождающего многочлена необходимо перемножить все многочлены fi (x), расположенные начиная от строки данного кода и выше, при том же n. Например, g(x) для кода (63,39) находится следующим образом:
Поле Галуа GF(2^4) по модулю П(А)=1+А+А^4
| Вес | |||||
Таблица сложения в поле GF(2^4)
Поле Галуа GF(2^5) по модулю П(А)=1+А^2+А^5
| Вес | ||||||
Таблица сложения в поле GF(2^5)
|
|
|
|
|
Дата добавления: 2014-01-14; Просмотров: 517; Нарушение авторских прав?; Мы поможем в написании вашей работы!
Генерация страницы за: 0.015 сек.