
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Становление и основные этапы развития графического дизайна в России и на Западе. Периодика
|
|
|
|
46.
24,25.
Упругие деформации однородного стержня.
При рассмотрении деформации любого тела, можно произвести мысленное разбиение этого тела на области, подобные однородному стержню. Затем можно рассмотреть деформацию каждой области в отдельности, после чего можно для всех областей такого тела сделать общий вывод о деформации всего тела.
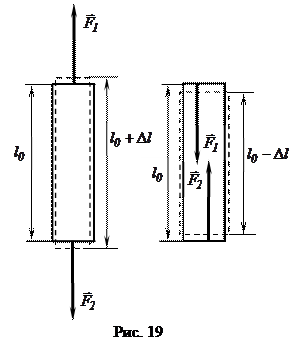 Однородные стержни ведут себя подобно пружине. При деформации стержень получает положительное приращение при растяжении и отрицательное при сжатии (рис. 19). Для стержня, подобно пружине, можно определить относительное удлинение.
Однородные стержни ведут себя подобно пружине. При деформации стержень получает положительное приращение при растяжении и отрицательное при сжатии (рис. 19). Для стержня, подобно пружине, можно определить относительное удлинение.
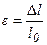 - относительное удлинение
- относительное удлинение
стержня.
Из опыта определено:
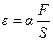 , где
, где 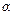 - коэффициент упругой
- коэффициент упругой
податливости, 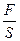 - давление, оказываемое на стержень (механическое напряжение).
- давление, оказываемое на стержень (механическое напряжение).
Примечание: из-за взаимодействия частей тела напряжение передаётся во все точки тела. Поэтому при продольном растяжении создаётся ещё и поперечное упругое сжатие, связанное с изменением толщины стержня, и наоборот, при продольном сжатии создаётся поперечное упругое растяжение (рис. 19).
| Напряжение | |
Нормальное 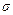 (деформирующая сила направлена по нормали (рис. 19) к поверхности тела).
Возникает деформация сжатия (растяжения).
(деформирующая сила направлена по нормали (рис. 19) к поверхности тела).
Возникает деформация сжатия (растяжения).
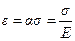 , где E – модуль Юнга[13]. , где E – модуль Юнга[13].
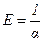 .
Физический смысл модуля Юнга: модуль Юнга равен такому нормальному напряжению, при котором относительное удлинение равно 1.
Можно получить закон Гука для такого вида деформации.
Закон Гука: .
Физический смысл модуля Юнга: модуль Юнга равен такому нормальному напряжению, при котором относительное удлинение равно 1.
Можно получить закон Гука для такого вида деформации.
Закон Гука: 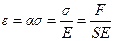 Þ
Þ Þ
Þ 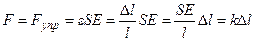 ;
или: ;
или:
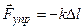 , где k – постоянная , где k – постоянная
| Тангенциальное  (деформирующая сила направлена по касательной (рис. 20) к поверхности тела).
Возникает деформация сдвига.
Пусть дано тело в виде прямоугольного параллелепипеда, к которому приложены силы
(деформирующая сила направлена по касательной (рис. 20) к поверхности тела).
Возникает деформация сдвига.
Пусть дано тело в виде прямоугольного параллелепипеда, к которому приложены силы 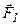 и и 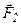 , такие что , такие что 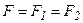 . Тогда, в любом
сечении, параллельном противоположным граням, на которые действуют эти силы, возникает тангенциальное механическое напряжение. . Тогда, в любом
сечении, параллельном противоположным граням, на которые действуют эти силы, возникает тангенциальное механическое напряжение.
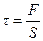 , где S – площадь грани.
В качестве характеристики сдвига берут: , где S – площадь грани.
В качестве характеристики сдвига берут:
|
| для данного стержня. | 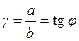 - относительный сдвиг. - относительный сдвиг.
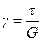 , где G – модуль сдвига.
Физический смысл модуля сдвига: модуль сдвига равен такому тангенциальному напряжению, при котором угол сдвига оказался бы равным 45°. , где G – модуль сдвига.
Физический смысл модуля сдвига: модуль сдвига равен такому тангенциальному напряжению, при котором угол сдвига оказался бы равным 45°.
|
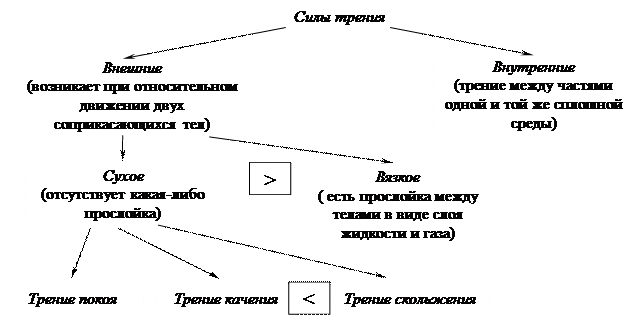
Сила трения.
26. Рассмотрим ещё один вид сил, который является следствием фундаментальных электромагнитных сил.
Силы, появляющиеся при перемещении соприкасающихся тел или их частей друг относительно друга – называются силами трения.
Причины возникновения трения между телами:
1. наличие шероховатости соприкасающихся поверхностей;
2. взаимодействие между атомами и молекулами тел.
Можно привести классификацию сил трения.
 Определим направление силы трения.
Определим направление силы трения.
Силы трения направлены, в основном, по касательным к трущимся поверхностям (или слоям), причём так, что они противодействуют относительному смещению этих поверхностей (слоёв).
Сухое трение.
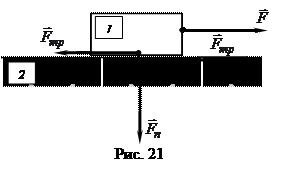 Пусть одно тело движется по другому телу (рис. 21).
Пусть одно тело движется по другому телу (рис. 21).
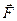 - внешняя сила, движущая тело 1.
- внешняя сила, движущая тело 1.
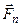 - сила нормального давления тела 1 на тело 2.
- сила нормального давления тела 1 на тело 2.
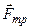 - сила трения тел 1 и 2.
- сила трения тел 1 и 2.
Примечание: для каждой конкретной пары тел и каждого значения силы нормального давления имеется определённое минимальное значение силы, при котором тело удаётся сдвинуть с места. До этого момента говорят о силе трения покоя.
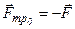 - сила трения покоя.
- сила трения покоя.
Существование силы трения покоя хорошо показывается с помощью III закона Ньютона. Если же внешняя сила превзойдёт по модулю силу трения покоя, то тело начнёт скользить. В этом случае говорят о силе трения скольжения.
Сила трения скольжения зависит (из опыта):
1. от природы трущихся поверхностей;
2. от состояния трущихся поверхностей.
 Закон сухого трения (закон Амонтона – Кулона): максимальная сила трения покоя, а также сила трения скольжения не зависят от площади соприкосновения трущихся тел и оказываются приблизительно пропорциональными величине силы нормального давления, прижимающей трущиеся поверхности друг к другу:
Закон сухого трения (закон Амонтона – Кулона): максимальная сила трения покоя, а также сила трения скольжения не зависят от площади соприкосновения трущихся тел и оказываются приблизительно пропорциональными величине силы нормального давления, прижимающей трущиеся поверхности друг к другу:
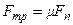 , где
, где 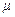 - коэффициент
- коэффициент
трения (покоя или скольжения).
В случае относительного скольжения гладких поверхностей закон трения записывается так:
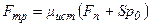 , где
, где 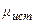 -
-
истинный коэффициент трения, 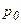 - добавочное давление, обусловленное притяжением молекул друг к другу, S – площадь соприкосновения поверхностей.
- добавочное давление, обусловленное притяжением молекул друг к другу, S – площадь соприкосновения поверхностей.
В случае скольжения, коэффициент трения является функцией скорости (рис. 22).
Сила трения скольжения и сила трения качения являются аналогичными силами, но коэффициент трения качения меньше коэффициента трения скольжения, что позволяет для уменьшения трения между поверхностями заменять скольжение качением.
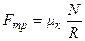 - сила трения качения, где R – радиус
- сила трения качения, где R – радиус
перекатывающегося тела.
Вязкое трение и сопротивление среды.
27. Кроме сухого трения существует также вязкое трение, которое имеет свои особенности.
Сила вязкого трения обращается в нуль одновременно со скоростью.
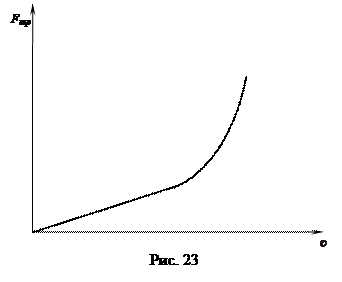 Рассмотрим силы трения между твёрдым телом и вязкой средой. Помимо сил трения, при движении тел в жидкой или газообразной среде возникают силы сопротивления среды.
Рассмотрим силы трения между твёрдым телом и вязкой средой. Помимо сил трения, при движении тел в жидкой или газообразной среде возникают силы сопротивления среды.
При малых скоростях:
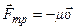 , где
, где 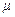 - коэффициент
- коэффициент
вязкого трения, зависящий от формы и размеров тела, состояния его поверхностей, вязкости (рис. 23).
Примечание: знак «минус» означает, что эта сила направлена противоположно скорости.
При больших скоростях:
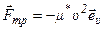 , где
, где 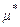 - коэффициент
- коэффициент
вязкого трения, зависящий от формы и размеров тела (рис. 23).
Значение скорости, при которой зависимость силы вязкого трения от скорости переходит от линейной к квадратичной (рис. 23), зависит от:
1. размеров и формы тела;
2. вязких свойств среды;
3. плотности среды.
Подробнее вязкое трение будет изучаться после рассмотрения строения вещества.
Сила тяжести и вес тела.
28. Любое тело, находящееся около поверхности Земли или на её поверхности притягивается к ней с некоторой силой, называемой силой тяжести.
Сила, с которой все тела притягиваются к Земле, находясь на её поверхности или вблизи её, называется силой тяжести.
Если отпустить тело на некоторой высоте от поверхности Земли, то оно будет падать с ускорением свободного падения 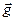 , причём:
, причём:
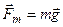 - сила тяжести.
- сила тяжести.
Определим точку приложения силы тяжести и её направление.
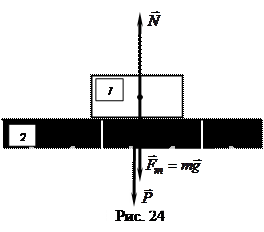 Точка приложения силы тяжести – центр масс тела.
Точка приложения силы тяжести – центр масс тела.
Направление силы тяжести – на центр Земли.
Если тело покоится относительно Земли на какой-либо поверхности, то это означает, что поверхность действует на тело с силой 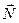 , называемой реакцией опоры. Но по III закону Ньютона тело должно действовать на опору с силой
, называемой реакцией опоры. Но по III закону Ньютона тело должно действовать на опору с силой 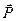 (рис. 24).
(рис. 24).
Сила, с которой тело действует на опору или подвес, называется весом тела.
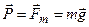 - вес тела в случае,
- вес тела в случае,
если тело находится на неподвижной опоре или неподвижном подвесе, а также, если опора или подвес движутся по инерции.
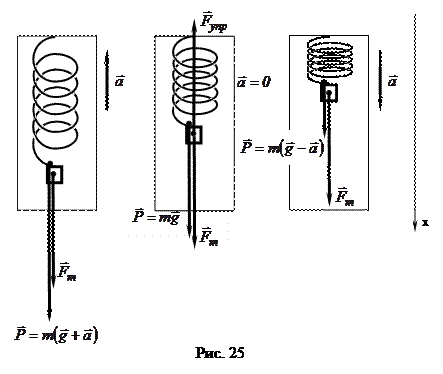 Следует заметить: несмотря на то, что для веса и силы тяжести записана одна и та же формула, нельзя отождествлять эти силы. Это силы, приложенные к разным телам, имеющие разные точки приложения. Модуль силы тяжести и модуль веса также могут отличаться друг от друга. Пусть подвес в виде пружины, укреплённой на рамке, движется вместе с телом с ускорением
Следует заметить: несмотря на то, что для веса и силы тяжести записана одна и та же формула, нельзя отождествлять эти силы. Это силы, приложенные к разным телам, имеющие разные точки приложения. Модуль силы тяжести и модуль веса также могут отличаться друг от друга. Пусть подвес в виде пружины, укреплённой на рамке, движется вместе с телом с ускорением 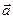 (рис. 25). Тогда, применяя II закон Ньютона, получаем:
(рис. 25). Тогда, применяя II закон Ньютона, получаем:
 Þ
Þ
Þ 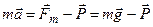 ;
;
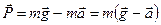 .
.
Переходя к проекциям векторов ускорений, учитывая свойства векторов и их проекций[14]
получаем:
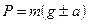 , где знак «плюс» ставится в том случае, если
, где знак «плюс» ставится в том случае, если
ускорение 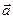 направлено вверх, а «минус» если
направлено вверх, а «минус» если 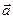 направлено вниз.
направлено вниз.
Примечание: если тело свободно падает то 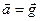 , и
, и 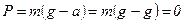 , откуда следует, что тело находится в состоянии невесомости.
, откуда следует, что тело находится в состоянии невесомости.
Соотношение 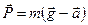 между массой и весом тела даёт способ сравнения масс тел путём взвешивания, так как для одной и той же точки Земли верно соотношение:
между массой и весом тела даёт способ сравнения масс тел путём взвешивания, так как для одной и той же точки Земли верно соотношение:
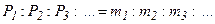 - принцип определения масс тел путём
- принцип определения масс тел путём
их взвешивания.
Примечание: ускорение свободного падения есть, вообще говоря, величина изменяющаяся, которая зависит от:
- географической широты местности;
- расстояния от центра Земли.
§ 16. Динамика вращательного движения.
 29. Теперь рассмотрим важный случай в механике – случай вращения тела. При рассмотрении поступательного движения тела можно было выбрать произвольную точку этого тела, и описать движение этой точки, предполагая, что так движутся все точки поступательно движущегося тела. Таким образом, описание поступательного движения тела в целом можно свести к описанию движения любой точки этого тела.
29. Теперь рассмотрим важный случай в механике – случай вращения тела. При рассмотрении поступательного движения тела можно было выбрать произвольную точку этого тела, и описать движение этой точки, предполагая, что так движутся все точки поступательно движущегося тела. Таким образом, описание поступательного движения тела в целом можно свести к описанию движения любой точки этого тела.
При рассмотрении вращательного движения тела обнаруживается, что все точки такого тела движутся различным образом, а именно: имеют различные траектории, скорости, совершают различные перемещения и т. д. Мысленно разбив тело на большое количество частиц, можно описать криволинейное движение каждой частицы в отдельности.
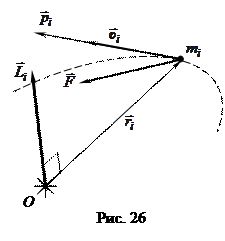
Пусть некоторая частица движется по криволинейной траектории относительно точки O. Такое движение возможно, если на частицу действует сила 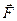 . Положение частицы задаётся радиусом - вектором, частица имеет массу и скорость (рис. 26). Каждый участок криволинейной траектории частицы можно охарактеризовать радиусом кривизны. Для такой частицы можно определить её импульс. Но есть ещё одна величина, которая характеризует движение частицы – это момент импульса.
. Положение частицы задаётся радиусом - вектором, частица имеет массу и скорость (рис. 26). Каждый участок криволинейной траектории частицы можно охарактеризовать радиусом кривизны. Для такой частицы можно определить её импульс. Но есть ещё одна величина, которая характеризует движение частицы – это момент импульса.
 Векторная величина, являющаяся динамической характеристикой вращательного движения, равная векторному произведению радиуса - вектора частицы относительно некоторой точки и импульса этой частицы, называется моментом импульса частицы относительно некоторой точки.
Векторная величина, являющаяся динамической характеристикой вращательного движения, равная векторному произведению радиуса - вектора частицы относительно некоторой точки и импульса этой частицы, называется моментом импульса частицы относительно некоторой точки.
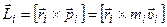 .
.
Момент импульса частицы относительно выбранной точки есть величина псевдовекторная, направление которой находится по правилу правого винта: если вращать винт от вектора 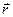 к вектору
к вектору 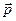 по наименьшему углу, то направление поступательного движения этого винта укажет направление вектора
по наименьшему углу, то направление поступательного движения этого винта укажет направление вектора 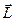 (рис. 26).
(рис. 26).
Модуль момента импульса частицы относительно выбранного начала отсчёта:
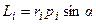 , где
, где 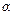 - угол между радиусом –
- угол между радиусом –
вектором и вектором импульса частицы.
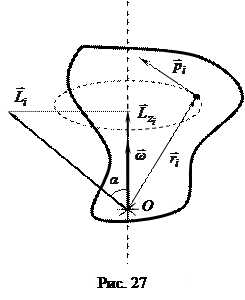
Если рассматривать вращающееся твёрдое тело, то его можно представить в виде системы частиц, каждая из которых движется по окружности (рис. 27), тогда для каждой частицы можно определить момент импульса относительно выбранного начала отсчёта. Складывая (геометрически) моменты импульсов всех точек тела, можно найти момент импульса всего тела в целом.
Момент импульса тела (системы частиц) относительно выбранной точки:
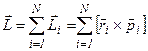 .
.
Чаще для вращающегося тела применяют не момент импульса этого тела относительно некоторой точки, а момент импульса тела относительно оси вращения.
Моментом импульса тела (системы частиц) относительно неподвижной оси называют проекцию на эту ось момента импульса тела (системы частиц) относительно некоторой неподвижной точки принадлежащей этой оси (рис. 27):
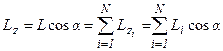 .
.
Примечание: иногда момент импульса тела относительно неподвижной оси представляют в виде вектора  (рис. 27).
(рис. 27).
 Введём ещё одну динамическую величину, характеризующую воздействие внешних тел на рассматриваемое вращающееся тело.
Введём ещё одну динамическую величину, характеризующую воздействие внешних тел на рассматриваемое вращающееся тело.
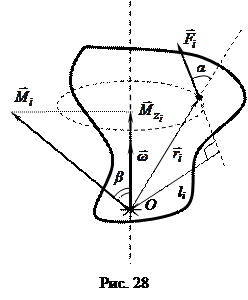
Векторная величина, характеризующая способность силы вращать тело вокруг неподвижной точки, численно равная векторному произведению радиуса – вектора частицы и силы, приложенной к этой частице, называется моментом силы (рис. 28):
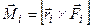 .
.
Модуль момента силы частицы относительно неподвижной точки:
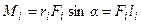 - где
- где 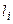 является
является
плечом момента силы частицы относительно неподвижной точки.
Направление вектора момента силы частицы относительно неподвижной точки определяется по правилу правого винта, который нужно вращать по наименьшему углу от радиуса – вектора к вектору силы. Тогда, поступательное движение такого винта укажет направление момента силы.
 Подобно тому, как наряду с моментом импульса частицы относительно неподвижной точки применяют момент импульса частицы относительно неподвижной оси, так и наряду с моментом силы относительно точки применяют момент силы относительно оси.
Подобно тому, как наряду с моментом импульса частицы относительно неподвижной точки применяют момент импульса частицы относительно неподвижной оси, так и наряду с моментом силы относительно точки применяют момент силы относительно оси.
Моментом силы, приложенным к частице, относительно неподвижной оси называют проекцию момента силы частицы относительно неподвижной точки, лежащей на этой оси (рис. 28):
 .
.
Примечание: иногда момент силы частицы относительно неподвижной оси представляют в виде вектора 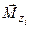 (рис. 28).
(рис. 28).
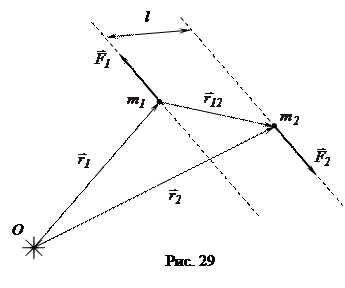
Пусть на две произвольные точки тела действуют две силы, противоположные по направлению, но одинаковые по модулю. Казалось бы, что такое тело должно находиться в состоянии равновесия по II закону Ньютона, но так бывает не всегда. Если эти силы не находятся на одной прямой, то тело под действием этих сил придёт во вращение. Говорят, что в этом случае на тело действует пара сил.
Две равные по величине противоположно направленные силы, не действующие вдоль одной прямой, называются парой сил, а расстояние между прямыми, вдоль которых действуют силы, называется плечом пары (рис. 29).
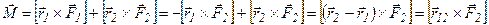 - момент
- момент
пары сил.
Модуль момента пары сил:
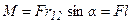 , где
, где 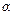 - наименьший угол между вектором
- наименьший угол между вектором
силы и 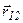 , а l – плечо момента пары сил.
, а l – плечо момента пары сил.
Примечание: момент пары сил не зависит от выбора точки, относительно которой он вычисляется.
Движение центра масс тела.
30. Пусть имеется некоторое тело, которое мы будем считать абсолютно твёрдым. Для исследования движения этого тела мысленно разобьём его на элементарные массы 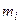 , каждую из которых можно принять за материальную точку. Взаимное расположение этих материальных точек не изменяется. Запишем для каждой
, каждую из которых можно принять за материальную точку. Взаимное расположение этих материальных точек не изменяется. Запишем для каждой 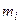 II закон Ньютона:
II закон Ньютона:
Второй закон Ньютона для каждой частицы абсолютно твёрдого тела:
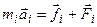 , где
, где 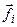 - результирующая всех внутренних сил,
- результирующая всех внутренних сил,
действующих на частицу, а 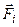 - результирующая всех внешних сил, действующих на эту же частицу.
- результирующая всех внешних сил, действующих на эту же частицу.
Полученные уравнения для каждой частицы нужно сложить, тогда получим II закон Ньютона для всего тела. При этом нужно учесть, что сумма внутренних сил в твёрдом теле равна нулю.
Второй закон Ньютона для всего твёрдого тела:
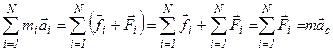 , где m – масса всего
, где m – масса всего
твёрдого тела, а 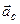 - ускорение точки этого тела, которая называется центром масс.
- ускорение точки этого тела, которая называется центром масс.
Полученное выше выражение позволяет представить импульс системы частиц в виде произведения суммарной массы частиц на скорость центра масс системы.
Импульс центра масс тела:
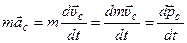 Þ
Þ  .
.
Центром масс (инерции) системы частиц (тела) называется точка, положение которой задаётся радиусом – вектором:
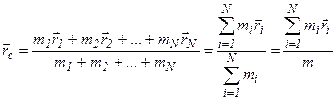 .
.
Декартовы координаты центра масс системы определяются проекциями 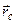 на координатные оси.
на координатные оси.
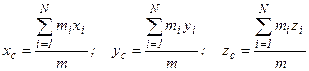 - декартовы координаты
- декартовы координаты
центра масс.
Примечание: в однородном поле сил тяжести центр инерции совпадает с центром тяжести системы.
Зная импульс центра масс системы, можно определить скорость движения центра масс.
Скорость движения центра масс системы:
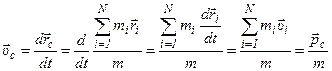 .
.
Если 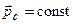 , то центр инерции системы либо движется прямолинейно и равномерно, либо остаётся неподвижным.
, то центр инерции системы либо движется прямолинейно и равномерно, либо остаётся неподвижным.
Центр масс твёрдого тела движется так, как двигалась бы материальная точка с массой, равной массе тела, под действием всех приложенных к телу сил.
Основной закон динамики вращательного движения.
31. Получим основной закон динамики вращательного движения тела. Для этого умножим векторно слева II закон Ньютона для каждой частицы этого тела, а затем сложим полученные уравнения.
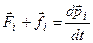 Þ
Þ 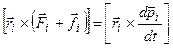 Þ
Þ 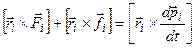 Þ
Þ
Þ 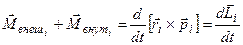 - для каждой частицы тела;
- для каждой частицы тела;
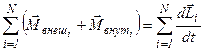 Þ
Þ 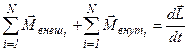 - для всего тела в целом.
- для всего тела в целом.
Так как сумма моментов внутренних сил в абсолютно твёрдом теле равна нулю, то:
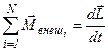 .
.
Полученное выражение представляет собой закон динамики для вращающегося тела (аналог II закона Ньютона для поступательно движущегося тела).
1-я формулировка: скорость изменения момента импульса тела равна геометрической сумме действующих на тело моментов сил:
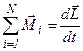 .
.
Произведём некоторые преобразования момента импульса частицы тела.
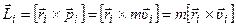 - для каждой частицы тела.
- для каждой частицы тела.
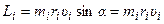 - так как все частицы абсолютно
- так как все частицы абсолютно
твёрдого тела движутся по окружностям, то 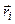 и
и 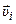 для всех частиц взаимноперпендикулярны, следовательно
для всех частиц взаимноперпендикулярны, следовательно  .
.
Заменив скорость частицы по формуле связи линейной и угловой скорости, получим:
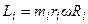 - где Ri радиус траектории частицы тела.
- где Ri радиус траектории частицы тела.
Найдём момент импульса тела относительно неподвижной оси.
Момент импульса частицы тела относительно неподвижной оси:
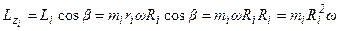 ,где b - угол между
,где b - угол между
моментом импульса частицы и осью вращения, а 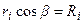 .
.
Момент импульса тела относительно неподвижной оси:
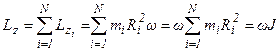 , где
, где 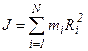 - момент
- момент
инерции тела относительно выбранной неподвижной оси.
Примечание: проекция момента импульса частицы относительно выбранной точки на некоторую ось не зависит от того, где именно на оси расположена эта точка.
С учётом вышеизложенных преобразований и выводов, запишем закон динамики вращающегося тела в иной формулировке.
Если момент импульса тела относительно неподвижной оси по направлению совпадает с направлением угловой скорости, то:
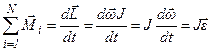 - получили вторую формулировку
- получили вторую формулировку
закона динамики вращательного движения.
2-я формулировка: момент внешних сил, действующих на тело, равен произведению момента инерции тела относительно оси вращения и углового ускорения этого тела:
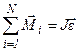 .
.
Момент инерции тела (системы частиц) относительно выбранной оси.
32. Рассмотрим понятие момента инерции тела (системы частиц) относительно выбранной оси.
Величина, характеризующая инертность тела при вращении его относительно некоторой оси, и численно равная сумме произведений масс частей тела и квадратов расстояний от этих частей до оси вращения, называется моментом инерции тела относительно некоторой оси.
Из определения момента инерции видно, что эта величина является аддитивной.
Момент инерции тела относительно выбранной оси равен сумме моментов инерции его частей относительно этой же оси:
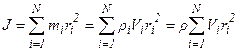 , где
, где 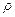 - плотность вещества.
- плотность вещества.
Полученное выражение тем точнее, чем меньше части, на которые разбивается тело.
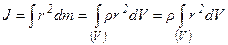 - момент инерции тела относительно
- момент инерции тела относительно
выбранной оси вращения, в случае неравномерно распределённой массы.
До сих пор мы говорили о вращении тела вокруг неподвижной оси. Это достаточно важный случай вращательного движения, который применяется в технике. Для того, чтобы ось вращения была неподвижной, её нужно удерживать с помощью внешних сил. Но есть такие оси вращения у тел, которые остаются неподвижными и в случае отсутствия внешних воздействий на эти оси.
Ось, положение которой в пространстве остаётся неизменным при вращении вокруг неё тела в отсутствие внешних сил, называется свободной осью тела.
Три взаимноперпендикулярные, проходящие через центр масс тела оси, которые могут служить свободными осями, называются главными осями инерции тела.
Моменты инерции относительно главных осей называются главными моментами инерции тела [15].
Моменты инерции однородных тел простейших
(симметричных) форм относительно
некоторых осей.
| Тело | Положение оси | Момент инерции |
| Полый тонкостенный цилиндр (кольцо) радиусом R и массой m | Ось проходит через центр масс тела перпендикулярно его основаниям |
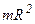
|
| Полый тонкостенный цилиндр (кольцо) внешним радиусом R1, внутренним радиусом R2 и массой m | Ось проходит через центр масс тела перпендикулярно его основаниям |
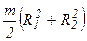
|
| Сплошной цилиндр (диск) радиусом R и массой m | Ось проходит через центр масс тела перпендикулярно его основаниям |
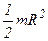
|
| Сплошной диск радиусом R и массой m | Ось проходит через центр масс тела и лежит в его плоскости |

|
| Сплошной шар радиусом R и массой m | Ось проходит через центр масс шара |
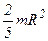
|
| Тонкостенная сфера радиусом R и массой m | Ось проходит через центр масс сферы |
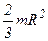
|
| Прямой тонкий стержень длиной l и массой m | Ось перпендикулярна стержню и проходит через его середину |
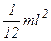
|
| Балка (прямоугольный стержень) длиной l, шириной d и массой m | Ось перпендикулярна балке и проходит через её середину |
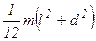
|
| Куб со стороной d и массой m | Ось проходит через центр масс и перпендикулярна стороне куба |
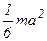
|
| Прямой тонкий стержень длиной l и массой m | Ось перпендикулярна стержню и проходит через его конец |
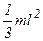
|
Теорема Гюйгенса-Штейнера.
33. Для вычисления моментов инерции тел относительно осей, не проходящих через центр инерции, используют теорему Гюйгенса-Штейнера.
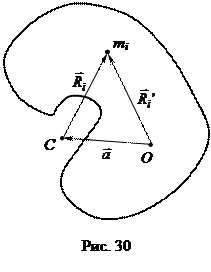 Теорема Гюйгенса-Штейнера: момент инерции тела относительно произвольной оси равен сумме момента инерции этого тела, относительно оси параллельной данной и проходящей через центр масс тела, и произведения массы тела и квадрата расстояния между осями (рис.30):
Теорема Гюйгенса-Штейнера: момент инерции тела относительно произвольной оси равен сумме момента инерции этого тела, относительно оси параллельной данной и проходящей через центр масс тела, и произведения массы тела и квадрата расстояния между осями (рис.30):
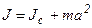 .
.
Доказательство: Пусть для рассматриваемого тела выделена ось, проходящая через точку O, тогда можно определить ось, проходящую через центр масс тела C и параллельную выбранной оси. Расстояние между осями равно a. Пусть 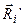 - вектор, соединяющий ось, проходящую через точку O, с массой произвольной частицы тела mi по кратчайшему расстоянию, а
- вектор, соединяющий ось, проходящую через точку O, с массой произвольной частицы тела mi по кратчайшему расстоянию, а 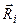 такой же, по сути, вектор, соединяющий ось, проходящую через центр масс, с этой же массой (рис. 30). Тогда:
такой же, по сути, вектор, соединяющий ось, проходящую через центр масс, с этой же массой (рис. 30). Тогда:
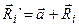 .
.
Возведём в квадрат полученную сумму:
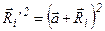 Þ
Þ 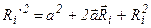 .
.
Умножив полученное выражение на массу рассматриваемой частицы тела, имеем:
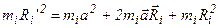 .
.
Аналогичные выражения можно найти для каждой частицы тела, тогда, для всего тела в целом запишем:
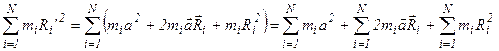 .
.
Так как:
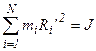 - момент инерции относительно произвольной оси (проходящей через точку O);
- момент инерции относительно произвольной оси (проходящей через точку O);
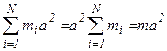 - произведение массы тела и квадрата расстояния между выбранной осью и осью, проходящей через центр масс, параллельно выбранной;
- произведение массы тела и квадрата расстояния между выбранной осью и осью, проходящей через центр масс, параллельно выбранной;
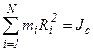 - момент инерции тела относительно оси, проходящей через центр масс тела, параллельно выбранной оси, то:
- момент инерции тела относительно оси, проходящей через центр масс тела, параллельно выбранной оси, то:
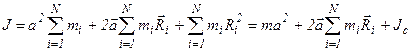 .
.
Второе слагаемое 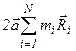 равно нулю, потому что сумма
равно нулю, потому что сумма 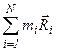 равна произведению массы тела и вектора
равна произведению массы тела и вектора 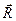 , проведённого от оси, проходящей через центр масс его, к самому центру масс, а, поскольку, центр масс лежит на этой оси, то
, проведённого от оси, проходящей через центр масс его, к самому центру масс, а, поскольку, центр масс лежит на этой оси, то 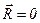 , и, следовательно,
, и, следовательно, 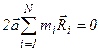 .
.
Тогда, окончательно, запишем:
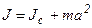 - что и требовалось доказать.
- что и требовалось доказать.
Примечание: если тело является однородным, то:
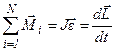 Þ
Þ 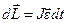 Þ
Þ 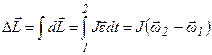 ,
,
тогда:
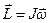 - откуда следует коллинеарность вектора угловой
- откуда следует коллинеарность вектора угловой
скорости и момента импульса. В общем случае эти вектора неколлинеарны, их связь задаётся уравнениями:
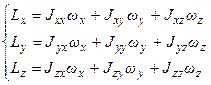 Þ момент инерции можно представить в виде тензора второго ранга (тензора инерции):
Þ момент инерции можно представить в виде тензора второго ранга (тензора инерции):
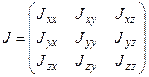 .
.
§ 17. Энергия. Работа. Мощность.
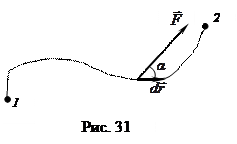 34. Пусть дана материальная точка, которая движется по некоторой траектории под действием силы
34. Пусть дана материальная точка, которая движется по некоторой траектории под действием силы 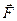 из положения 1 в положение 2 (рис. 31). Запишем уравнение движения этой частицы:
из положения 1 в положение 2 (рис. 31). Запишем уравнение движения этой частицы:
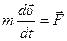 .
.
Умножим обе части этого уравнения на бесконечно малое перемещение 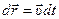 . Тогда:
. Тогда:

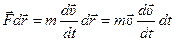 -получили
-получили
дифференциальное уравнение, которое нужно решить:
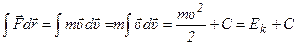 , где
, где 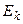 - кинетическая
- кинетическая
энергия материальной точки.
Кинетическую энергию можно найти и другими способами, используя выражение для нахождения импульса:
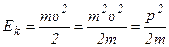 .
.
Если на тело действует сила, то кинетическая энергия изменяется со временем. Тогда говорят, что при перемещении частицы на 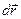 силой
силой 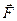 совершается элементарная работа:
совершается элементарная работа:
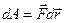 - элементарная работа, совершённая силой
- элементарная работа, совершённая силой 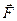 .
.
Работа – скалярная величина, характеризующая изменение энергии обусловленное действием силы на движущуюся частицу, численно равная скалярному произведению силы и перемещения тела, которое произошло под действием этой силы.
Используя определение скалярного произведения двух векторов, можно представить выражение для работы в следующем виде:
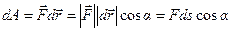 , где
, где 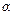 - угол между
- угол между 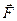 и
и 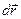 .
.
Отсюда следует, что работа может быть как положительной, так и отрицательной, а в некоторых случаях равна нулю:
1. если 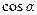 > 0 (при 0 ≤
> 0 (при 0 ≤ 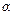 <
<  ), то A > 0 (работа положительна, а сила разгоняет тело);
), то A > 0 (работа положительна, а сила разгоняет тело);
2. если 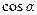 < 0 (при
< 0 (при  <
< 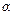 ≤
≤ 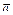 ), то A < 0 (работа отрицательна, сила тормозит тело);
), то A < 0 (работа отрицательна, сила тормозит тело);
3. если 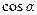 = 0 (при
= 0 (при 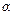 =
=  ), то A = 0 (работа не совершается);
), то A = 0 (работа не совершается);
4. если 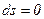 , то A = 0 (работа также не совершается);
, то A = 0 (работа также не совершается);
5. если F = 0, то A = 0 (работа не совершается, тело движется по инерции).
Единицы измерения работы.
Единицы измерения работы являются производными единицами:
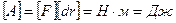 - в СИ;
- в СИ;
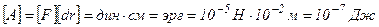 - в СГС.
- в СГС.
Теоремы о кинетической и потенциальной энергиях.
35. Работа является аддитивной величиной, то есть, для того, чтобы найти работу силы на всём пути, нужно сложить работы, совершённые на каждом участке этого пути. Сложение элементарных работ сводится к интегрированию.
Работа результирующей нескольких сил равна алгебраической сумме работ, совершаемых каждой из сил в отдельности:
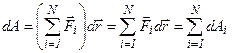 .
.
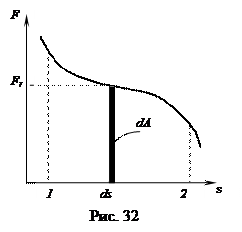 Вообще аддитивность работы хорошо видна при построении графика зависимости силы от пройденного пути (рис. 32). Так образом, при бесконечно малом перемещении под действием силы совершается элементарная работа, равная площади прямоугольника со сторонами
Вообще аддитивность работы хорошо видна при построении графика зависимости силы от пройденного пути (рис. 32). Так образом, при бесконечно малом перемещении под действием силы совершается элементарная работа, равная площади прямоугольника со сторонами 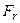 и ds. Вся же работа на пути от 1 до 2 будет находится как сумма площадей всех аналогичных прямоугольников, и в конечном счёте получим, что полная работа равна площади фигуры под графиком функции
и ds. Вся же работа на пути от 1 до 2 будет находится как сумма площадей всех аналогичных прямоугольников, и в конечном счёте получим, что полная работа равна площади фигуры под графиком функции 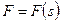 , ограниченной вертикальными линиями 1 и 2.
, ограниченной вертикальными линиями 1 и 2.
Тогда:
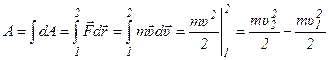 - полная работа на всём пути из положения 1 в положение 2.
- полная работа на всём пути из положения 1 в положение 2.
Таким образом, доказали теорему о кинетической энергии материальной точки.
Работа результирующей всех сил, действующих на частицу, идёт на приращение [16] кинетической энергии частицы:
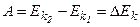 .
.
Теперь найдём работу, совершённую деформированной пружиной:
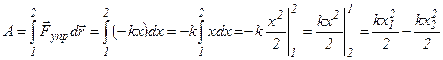 - работа деформированной
- работа деформированной
пружины.
Аналогичным образом можно поступить в случае нахождения работы, совершённой упруго деформированным стержнем:
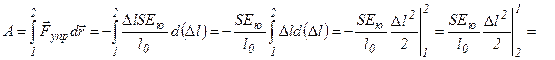
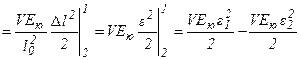 - работа деформированного
- работа деформированного
стержня, где Eю.- модуль Юнга.
Теперь найдём работу силы тяжести при падении тела с некоторой высоты:
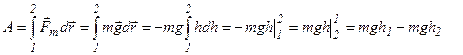 - работа силы
- работа силы
тяжести.
Во всех трёх случаях работа совершается так называемыми консервативными силами. Здесь же видим, что работа равна убыли некоторой величины, называемой потенциальной энергией. Полученное утверждение называют теоремой о потенциальной энергии.
Работа, совершаемая консервативными силами над телом, равна убыли потенциальной энергии тела:
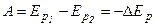 .
.
Примечание: из полученных теорем о кинетической и потенциальной энергиях видно, что единицы измерения энергии и единицы измерения работы совпадают.
Выражение для элементарной работы можно представить в следующем виде:
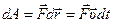 ,
,
Тогда полная работа равна:
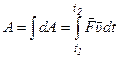 .
.
Изменение кинетической или потенциальной энергии может происходить с различной скоростью. Это означает, что работа также имеет скорость совершения. Величина, характеризующая эту скорость называется мощностью:
Мощность – скалярная физическая величина, характеризующая быстроту совершения работы, численно равная отношению работы ко времени, за которое она была совершена:
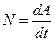 .
.
Можно получить также:
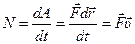 .
.
Единицы измерения мощности.
Единицы измерения мощности являются производными единицами:
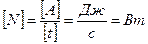 - в СИ;
- в СИ;
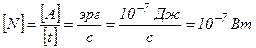 - в СГС;
- в СГС;
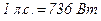 - внесистемная единица измерения мощности.
- внесистемная единица измерения мощности.
Потенциальное поле сил.
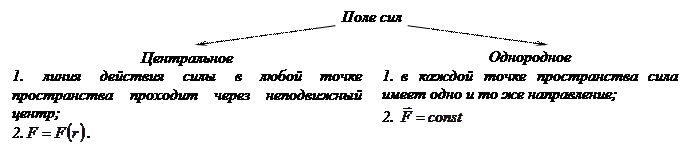 36. Если частица в каждой точке пространства подвержена воздействию других тел, то она находится в поле сил, действующих со стороны этих тел.
36. Если частица в каждой точке пространства подвержена воздействию других тел, то она находится в поле сил, действующих со стороны этих тел.
Если силовое поле можно описать с помощью функции 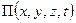 , такой что:
, такой что:
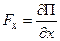 ;
; 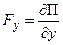 ;
; 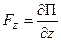 , то оно является потенциальным,
, то оно является потенциальным,
где Π – потенциал силового поля.
 Примечание: потенциал определяется с точностью до произвольной аддитивной постоянной.
Примечание: потенциал определяется с точностью до произвольной аддитивной постоянной.
Если поле стационарно, то:
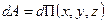 .
.
В случае потенциального силового поля имеем:
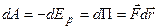 , откуда следует:
, откуда следует:
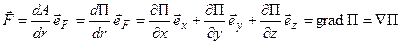 [17] - сила потенциального
[17] - сила потенциального
силового поля.
Работа силового поля определяется так:
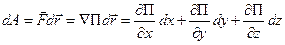 - работа потенциального
- работа потенциального
силового поля.
 Работа сил потенциального силового поля не зависит от формы траектории, вдоль которой движется частица, а зависит только от начального и конечного положения частицы.
Работа сил потенциального силового поля не зависит от формы траектории, вдоль которой движется частица, а зависит только от начального и конечного положения частицы.
Примечание: частным случаем неконсервативных сил являются диссипативные силы, отличительной особенностью которых является то, что они направлены в противоположную сторону скорости движения тела.
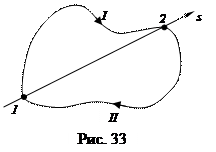 Примечание: работа консервативных сил на замкнутой траектории равна нулю.
Примечание: работа консервативных сил на замкнутой траектории равна нулю.
Пусть произвольный замкнутый путь произвольно разбит на две части (рис. 33). Тогда работа на всём пути будет равна сумме работ, совершаемых на каждом из участков:
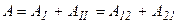 .
.
Из рисунка видно, что перемещения в проекциях на выбранную ось на I и II участках имеют разные знаки. Кроме того, поскольку силы консервативны, а их работа не зависит от формы траектории, следовательно:
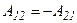
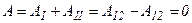 - на замкнутом пути.
- на замкнутом пути.
Потенциальная энергия во внешнем поле сил.
 37. Выше уже было упомянуто о двух видах механической энергии – кинетической и потенциальной.
37. Выше уже было упомянуто о двух видах механической энергии – кинетической и потенциальной.
Работа, совершаемая силой стационарного потенциального поля, определяется следующим образом:
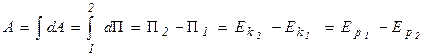 , откуда видно,
, откуда видно,
что 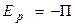 .
.
Тогда:
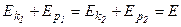 - полная механическая энергия.
- полная механическая энергия.
Отсюда видно, что понятие потенциальной энергии имеет большое значение. Связь между потенциальной энергией и силой потенциального поля имеет следующий вид:
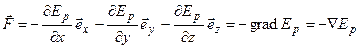
Сила, действующая на частицу в стационарном потенциальном силовом поле, равна градиенту потенциальной энергии, взятому с обратным знаком, а её компоненты равны:
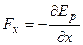 ;
; 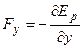 ;
; 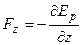 .
.
Свойства потенциальной энергии.
1. Потенциальная энергия определяется с точностью до произвольной постоянной.
2. Нулевой (начальный) уровень потенциальной энергии выбирается условно.
3. Конкретное выражение для вычисления потенциальной энергии зависит от характера силового поля:
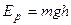 - потенциальная энергия поля силы тяжести;
- потенциальная энергия поля силы тяжести;
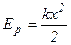 - потенциальная энергия упруго деформированной пружины;
- потенциальная энергия упруго деформированной пружины;
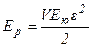 - потенциальная энергия упруго деформированного стержня;
- потенциальная энергия упруго деформированного стержня;
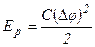 - потенциальная энергия заряженного конденсатора.
- потенциальная энергия заряженного конденсатора.
4. Потенциальная энергия может принимать как положительные, так и отрицательные значения (в отличие от кинетической энергии, которая всегда положительна).
§ 18. Кинетическая энергия вращающегося твёрдого тела.
 38. Пусть тело вращается вокруг неподвижной оси (рис. 34). Мысленно разобьём тело на большое количество частиц – элементарных масс. Для некоторой элементарной массы mi линейная скорость определяется как
38. Пусть тело вращается вокруг неподвижной оси (рис. 34). Мысленно разобьём тело на большое количество частиц – элементарных масс. Для некоторой элементарной массы mi линейная скорость определяется как 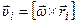 , или
, или 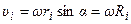 . Тогда:
. Тогда:
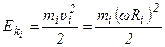 - кинетическая энергия
- кинетическая энергия
выделенной частицы вращающегося тела.
Тогда кинетическая энергия всего вращающегося тела:
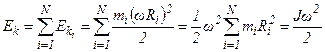 - кинетическая
- кинетическая
энергия вращающегося тела относительно неподвижной оси.
Пусть на mi действует внутренняя сила 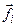 и внешняя сила
и внешняя сила 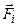 , которые совершают работу, тогда:
, которые совершают работу, тогда:
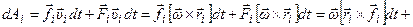
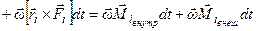 .
.
Для всего тела:
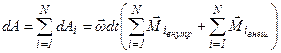 - элементарная работа,
- элементарная работа,
совершаемая над вращающимся телом.
Так как сумма моментов внутренних сил равна нулю, то:
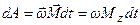 .
.
Учитывая, что  , получим:
, получим:
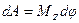 - работа внешних сил, вращающих тело.
- работа внешних сил, вращающих тело.
Примечание: все полученные формулы для вращательного движения аналогичны формулам для поступательного движения.
Пусть тело вращается произвольным образом. Если рассматривать вращение тела относительно системы координат, начало которой помещено в центр инерции тела, то:
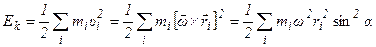
Представив 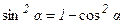 и учитывая, что
и учитывая, что 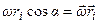 получим:
получим:
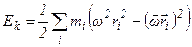 .
.
Расписав скалярные произведения через проекции 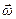 и
и 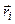 на оси координат:
на оси координат:
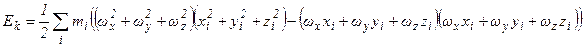 .
.
Раскрыв скобки и объединив слагаемые с одинаковыми произведениями компонент скорости, получим:
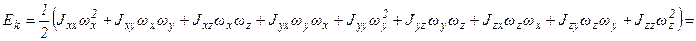
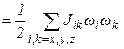 - кинетическая энергия вращающегося тела
- кинетическая энергия вращающегося тела
относительно неподвижной точки, совпадающей с его центром масс.
Если оси связанной с телом системы координат выбрать так, что они совпали бы с главными осями инерции тела, то:
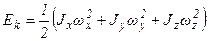 - кинетическая энергия
- кинетическая энергия
вращающегося тела если оси системы координат тела совпадают с главными осями инерции.
Вывод: Кинетическая энергия вращающегося тела равна половине произведения момента инерции тела относительно оси вращения и квадрата угловой скорости в трёх случаях:
1. для тела, вращающегося вокруг неподвижной оси;
2. для тела, вращающегося вокруг одной из главных осей инерции;
3. для шарового волчка.
Кинетическая энергия тела при плоском движении.
39. Плоское движение тела может быть представлено как наложение двух движений – поступательного и вращательного[18].
Плоским движением тела называют такое движение, при котором все точки тела движутся в параллельных плоскостях.
Скорость i -ой элементарной массы будет определяться следующим образом:
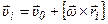 - скорость i-ой частицы, где
- скорость i-ой частицы, где 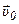 - скорость
- скорость
некоторой точки O, 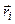 - радиус-вектор, определяющий положение элементарной массы по отношению к точке O.
- радиус-вектор, определяющий положение элементарной массы по отношению к точке O.
Тогда:
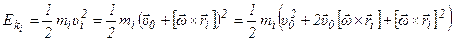 .
.
Так как 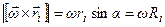 , и осуществив циклическую перестановку множителей во втором слагаемом, получим:
, и осуществив циклическую перестановку множителей во втором слагаемом, получим:
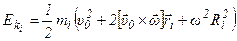
Кинетическая энергия всего тела при плоском движении:
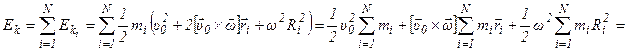
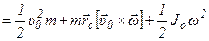 - кинетическая энергия тела при
- кинетическая энергия тела при
плоском движении.
Если в качестве точки O взять центр инерции, то 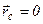 , тогда:
, тогда:
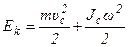 - кинетическая энергия тела при плоском
- кинетическая энергия тела при плоском
движении.
Кинетическая энергия тела при плоском движении слагается из энергии поступательного движения тела со скоростью, равной скорости центра инерции, и энергии вращения вокруг оси, проходящей через центр инерции тела.
§ 19. Законы сохранения.
40. Выделим для рассмотрения некоторую систему тел. На тела, входящие в эту систему, может действовать сила со стороны других тел, как входящих в систему, так и не принадлежащих ей.

| Внутренние (на тело действуют тела системы) | Внешние (на тело действуют тела, не принадлежащие системе) |
Система называется замкнутой (изолированной) если на неё не действуют внешние силы.
Для замкнутых систем существуют такие функции координат и скоростей частиц выбранной системы (интегралы движения), которые сохраняют при движении постоянные значения.
Для системы из N частиц можно найти 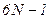 интегралов движения, но особый интерес представляют собой только следующие три аддитивные интегралы движения: энергия, импульс и момент импульса.
интегралов движения, но особый интерес представляют собой только следующие три аддитивные интегралы движения: энергия, импульс и момент импульса.
Аддитивными интегралами движения называются такие функции координат и скоростей частиц системы, что их значения для систем, состоящих из частей, взаимодействием которых можно пренебречь, равно сумме значений для каждой части в отдельности.

| Энергия | Импульс | Момент импульса |
| энергии следствие однородности времени (равнозначность всех моментов времени) | импульса следствие однородности пространства (одинаковость свойств пространства во всех его точках) | момента импульса следствие изотропии пространства (одинаковость свойств пространства по всем направлениям) |
Примечание: законы сохранения получаются из уравнений Ньютона, но они обладают гораздо большей общностью, чем законы Ньютона. Законы сохранения являются точными законами.
Часто бывает, что точное решение уравнений движения очень сложно. Но с помощью законов сохранения можно получить ряд важных данных о протекании механических явлений (даже если силы оказываются неизвестными).
Закон сохранения энергии.
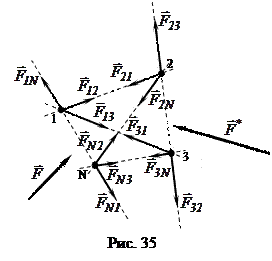 41. Рассмотрим систему, состоящую из N взаимодействующих частиц, где
41. Рассмотрим систему, состоящую из N взаимодействующих частиц, где  - силы взаимодействия между этими частицами, являющиеся неконсервативными (рис. 35). Пусть на систему тел действуют внешняя консервативная сила
- силы взаимодействия между этими частицами, являющиеся неконсервативными (рис. 35). Пусть на систему тел действуют внешняя консервативная сила  и внешняя неконсервативная сила
и внешняя неконсервативная сила  . Запишем для каждой частицы II закон Ньютона:
. Запишем для каждой частицы II закон Ньютона:
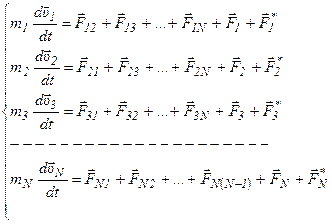 .
.
Примечание: так как частица не действует сама на себя, то слагаемые вида 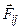 , где
, где  , отсутствуют.
, отсутствуют.
Умножим скалярно каждое уравнение на 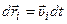 .
.
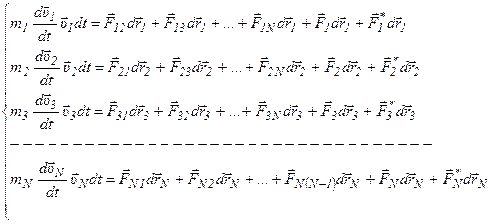 .
.
Сложим почленно все уравнения и получим:
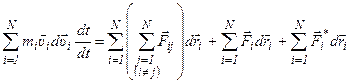 ;
;

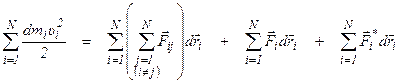 .
.
Таким образом, получим:
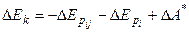 , или
, или 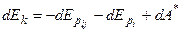 .
.
Тогда:
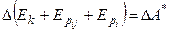 , или
, или  - полная энергия системы.
- полная энергия системы.
Если система замкнута, то работа внешних неконсервативных сил отсутствует.
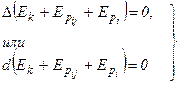 Þ
Þ 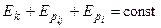 -
- 
Закон сохранения механической энергии: полная механическая энергия системы тел, на которые действуют лишь консервативные силы, остаётся постоянной.
Если же и потенциальная энергия внешнего силового поля не учитывается, то:
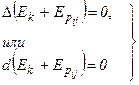 Þ
Þ 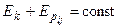 -
- 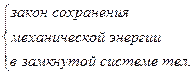
Закон сохранения механической энергии для замкнутой системы тел: полная механическая энергия замкнутой системы тел, между которыми действуют только консервативные силы, остаётся постоянной.
Ранее уже отмечалось, что законы сохранения имеют более общий смысл, а следовательно и более широкую область применения, чем законы Ньютона. Поэтому, закон сохранения энергии можно сформулировать и в более широком смысле.
Закон сохранения энергии: энергия ниоткуда не возникает и никуда не исчезает, она лишь преобразуется из одного вида в другой.
Равновесие механической системы.
42. С понятием энергии и законом сохранения энергии тесно связано понятие равновесия механической системы.
Если система тел находится в таком состоянии, что относительные скорости каждого тела равны нулю, а их потенциальные энергии имеют минимальные значения, то без воздействия извне тела системы не смогут прийти в движение, то есть, будут находиться в состояниях равновесия.
Состояние равновесия механической системы эквивалентно тому, что результирующая сила и результирующий момент сил, действующие на систему, равны нулю:
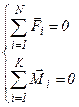 - условие равновесия механической системы.
- условие равновесия механической системы.
 | <
|
|
|
|
Дата добавления: 2014-01-14; Просмотров: 554; Нарушение авторских прав?; Мы поможем в написании вашей работы!
Генерация страницы за: 0.017 сек.