
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Движение тела
|
|
|
|
5.
Система единиц СИ.
| Величина | Единица СИ | ||||
| Наименование | Размерность | Наименование | Обозначение | Определение | |
| русское | м/н | ||||
| 1. Длина | L | метр | м | m | Единица длины, равная расстоянию, проходимому в вакууме плоской электромагнитной волной за 1/299792458 с |
| 2. Масса | M | килограмм | кг | kg | Единица массы равная массе международного прототипа |
| 3. Время | T | секунда | с | s | Единица времени, равная 9192631770 периодов излучения, соответствующего переходу между двумя сверхтонкими уровнями основного состояния атома Cs133 |
| 4. Сила тока | I | ампер | А | A | Сила неизменяющегося тока, проходящего по двум прямолинейным параллельным проводникам бесконечной длины и ничтожно малой площади кругового поперечного сечения расположенным на расстоянии 1 м один от другого в вакууме, который вызвал бы между этими проводниками силу 2·10-7 Н на каждый метр длины |
| 5. Термодина-мическая температура | Θ | кельвин | К | K | Единица измерения термодинамической температуры, равная 1/273,16 части термодинамической температуры тройной точки воды |
| 6. Количество вещества | N | моль | моль | mol | Единица количества вещества, равная количеству вещества системы, в которой содержится столько же структурных элементов, сколько содержится атомов в C12 массой 0.012 кг |
| 7. Сила света | J | кандела | кд | cd | Единица силы света, равная силе света в данном направлении от источника, испускающего монохроматический свет частотой 540·1012 Гц, сила излучения которого в этом направлении 1/683 Вт/ср |
| Дополнительные единицы СИ | |||||
| 8. Плоский угол | - | радиан | рад | rad | Угол между двумя радиусами окружности, длина дуги между которыми равна радиусу |
| 9. Телесный угол | - | стерадиан | ср | sr | Телесный угол с вершиной в центре сферы, вырезающий на поверхности её площадь, равную площади квадрата со стороной равной радиусу сферы |
§ 4. Основные этапы развития физики.
6. История физики хранит немало событий и фактов, оказавших большое влияние на ход развития этой древней науки и составивших золотой фонд её памяти. Размещённые в строгой временной последовательности, эти факты дают возможность проследить генезис основных физических идей и теорий, их взаимосвязь, преемственность и эволюцию, тенденции развития, а некоторые из них, в силу своей фундаментальной роли, открывают новые страницы в летописи физики, изменяя или дополняя научную картину природы. Существует определённая периодизация физики, дающая возможность более отчётливо представить структурные особенности и динамику развития физики, её идей и принципов.
I. Предыстория физики (от древнейших времён до XVII в.)
1. Эпоха античности (VI в. до н. э. - V в. н. э.) - период накопления физических знаний об отдельных явлениях природы (возникновение простейших методов измерений, наблюдения по акустике Пифагора, первые сведения об электричестве и магнетизме, полученные Фалесом Милетским, возникновение идеи о делимости вещества (Левкипп, Демокрит), получение первых знаний в механике, статике (Аристотель, Архимед), возникновение геометрической оптики (Евклид), построение систем мира).
2. Средние века (VI - XIV вв.) - уточнение физических знаний, развитие отдельных учений (работы по физиологической оптике Альхазена, другие работы по оптике (Вителло, Бэкон, Ал-Фаризи), развитие кинематики (Гейтсбери, Саксонский)).
3. Эпоха Возрождения (XV - XVI вв.) - дальнейшее развитие физических учений, возникновение новых учений (углубление знаний по механике, зарождение динамики, изучение трения, открытие явления капиллярности (Леонардо да Винчи), начало утверждения гелиоцентрической системы мира (Коперник), работы Галилея по изучению маятника, окончательное завершение статики (Стевин), изобретение новых приборов).
II. Период становления физики как науки (начало XVII в. - 80-е гг. XVII в.) - начало естествознания, активное изучение различных природных явлений, их описание и попытки объяснения - опыты Галилея с движущимися телами, принцип относительности Галилея, законы Кеплера, дальнейшее развитие геометрической оптики (Кеплер, Снеллиус), начало исследования тепловых явлений (Бэкон, Бойль, Гук и др.), открытие атмосферного давления (Торричелли), работы по гидростатике, открытие закона всемирного тяготения (Ньютон), конкурирование волновой теории света Гюйгенса и корпускулярной теории света Ньютона. [1]
III. Период классической физики (конец XVII в. - начало XX в.)
1. Первый этап (конец XVII в. - 60-е гг. XIX в.) - полное господство механики Ньютона, его механическая картина мира совершенствуется и уточняется, физика представляется уже целостной наукой (законы механики Ньютона, развитие волновой физики (Гюйгенс, Савёр), изучение электрических явлений (Гауксби, Грей, Дюфе, Кулон и др.), основы гидродинамики (Бернулли, Эйлер), начало молекулярно-кинетических представлений (Ломоносов), начало изучения электрического тока (Фуркруа, Никольсон, Риттер и др.), изучение волновых оптических явлений (Юнг, Френель, Фраунгофер и др.), изучение магнетизма и электрических токов (Эрстед, Ампер, Био, Савар, Лаплас, Ом и др.), формирование термодинамики (Карно, Уатт), открытие электромагнитной индукции (Фарадей), начало изучения теплового излучения (Кирхгоф)). [2]
2. Второй этап (60-е гг. XIX в. - 1894 г.) - создание общей строгой теории электромагнитных процессов с использованием концепции поля Фарадея (уравнения Максвелла, продолжение исследования теплового излучения (Кирхгоф, Стефан, Больцман, Вин), исследование электромагнитных волн и световых волн как электромагнитных (Максвелл, Лоренц), дальнейшее развитие статистической физики и физической кинетики (Максвелл, Больцман), начало изучения спектральных линий атомов (Бальмер, Ридберг), открытие и изучение фотоэффекта (Герц, Столетов и др.)).
3. Третий этап (1895 - 1904) - этап революционных изменений в физике (открытие Рентгеном нового излучения, исследование ферромагнетизма (Кюри), открытие естественной радиоактивности (Беккерель), открытие электрона (Томсон), открытие новых радиоактивных элементов (Кюри, Склодовская-Кюри), открытие альфа- и бета- гамма-лучей (Резерфорд, Виллар), формулирование гипотезы Планка, разработка моделей атома (Перрен, Томсон), преобразования координат и времени Лоренца). [3]
IV. Период современной физики (с 1905 г.)
1. Первый этап (1905 - 1931 гг.) - отход от классических представлений и понятий и начало создания новой физической картины мира - квантово-релятивистской (создание специальной теории относительности, квантовой теории светового излучения и фотоэффекта Эйнштейном, уравнения релятивистской динамики (Планк), работы по исследованию атома, начало исследования атомного ядра [4], общая теория относительности Эйнштейна, начало создания единой теории поля (Вейль), начало нелинейной оптики (Вавилов, Лёвшин), идея о волновых свойствах материи (де Бройль) [5], уравнение Шрёдингера, открытие дифракции электронов (Дэвиссон, Джермер, Томсон), основы квантовой электродинамики и квантовой теории поля (Дирак, Гейзенберг, Паули, Ферми)).
2. Второй этап (1932 - 1954 гг.) - этап субатомной физики, исследующий новый уровень материи - мир атомного ядра (открытие нейтрона (Чэдвик), осуществление ядерных превращений под действием нейтронов (Фезер, Мейтнер, Харкинс), открытие сильного взаимодействия, гипотеза о существовании антивещества (Дирак), открытие искусственной радиоактивности (Ф. и И. Жолио-Кюри, Ферми), завершено создание современной квантовой электродинамики (Томонага, Фейнман и др.), открытие ряда элементарных частиц, начало квантовой электроники (Басов, Прохоров, Таунс), построение современной электронной теории металлов (Лифшиц)).
3. Третий этап (с 1955 г.) - этап субъядерной физики и физики космоса (исследование структуры нуклонов (Хофштадтер), синтезирование новых элементов, выдвижение термоядерной теории образования химических элементов в звёздах (Фаулер, Хойл), начало исследований в области квантовой теории необратимых процессов (Ван-Хов, Кубо), исследование слабого взаимодействия, предложены схемы классификации частиц, разработка космических исследований, идея объединения слабых и электромагнитных взаимодействий (Швингер), дальнейшая разработка макроскопической теории сверхпроводимости (Бардин, Купер, Шриффер), теория туннельных эффектов в полупроводниках (Келдыш), теория магнитных свойств сверхпроводящих сплавов (Абрикосов), разработка принципа работы лазера (Таунс, Шавлов), исследование плазмы, созданы мощные сверхпроводящие магниты (Кюнцлер), выполнение голографических записей (Денисюк), выдвинута гипотеза кварков (Гелл-Манн, Цвейг)).
7. Основные направления исследований на современном этапе развития физики.
В настоящее время особое внимание уделяется следующим направлениям исследования в физике:
1. Физика элементарных частиц (существование кварков и глюонов в свободном состоянии, построение квантовой теории тяготения).
2. Астрофизика (состояние материи в «чёрных дырах», природа квазаров, причины вспышек сверхновых, состояние материи внутри звёзд).
3. Физика ядра (осуществление управляемого термоядерного синтеза, поиск долгоживущих элементов с порядковыми номерами 114 - 126, нет единой теории атомного ядра, построение теории сильных взаимодействий).
4. Квантовая электроника (повышение КПД лазеров, расширение диапазона длин волн с плавной перестройкой частоты).
5. Физика твёрдого тела (создание новых материалов с заданными свойствами, высокотемпературных сверхпроводников, например).
6. Физика плазмы (разогрев плазмы до 109 К и её удержание в течение времени, достаточного для протекания термоядерной реакции).
В соответствии с перечисленными направлениями физика имеет следующую структуру.
| - Механика твёрдого тела. | ||
| Физика элементарных частиц - | Ф | - Механика сплошных сред. |
| Физика ядра - | И | - Термодинамика и статистическая физика.. |
| - Электродинамика с оптикой. | ||
| Физика атомов и молекул - | З | - Теория тяготения. |
| Физика газов и жидкостей - | И | - Квантовая механика. |
| - Квантовая теория поля. | ||
| Физика твёрдого тела - | К | - Колебания и волны. |
| Физика плазмы - | А | - Прикладная физика. |
 
| ||
| По изучаемым объектам | По формам движения (процессам) |
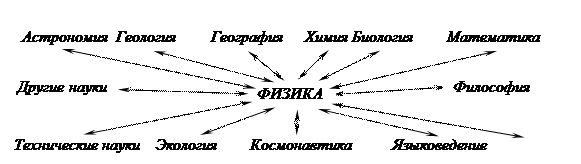
Связь физики с другими науками.
Физика не развивается отдельно от других наук. Она тесно связана со многими научными дисциплинами. В ряде случаев возникают даже пограничные науки, такие как: астрофизика, биофизика и др. Так С. И. Вавилов отмечал:«Физика глубочайшими корнями вросла в астрономию, геологию, химию, биологию и другие естественные науки». Многие науки используют результаты физических исследований, но и другие науки вносят большой вклад в развитие физики. Опять же С. И. Вавилов отмечал это на примере философии:«Предельная общность значительной части содержания физики, её фактов и законов искони сближала физику с философией… Иногда физические утверждения по своему характеру таковы, что их трудно отличить и отделить от философских утверждений, и физик обязан быть философом». Поэтому связь физики с другими науками носит двусторонний характер. И ещё надо отметить, что физика долгое время находилась на таком уровне теоретического обобщения, который другие науки долгое время не могли достичь. Вот так высказался по этому поводу Э. Резерфорд:«Все науки можно разделить на две группы - на физику и коллекционирование марок». Сейчас все науки подтягиваются к тому уровню на котором находится физика, и заслуги физики в этом очень велики, так как она снабдила их методами научного познания, теориями и т. д.
 |
Интересно рассмотреть вопрос о взаимосвязи физики с техникой. Этот вопрос прежде всего интересен для специалистов, которые в своей работе используют технику, потому что физика - фундаментальная база всех инженерных дисциплин, база для создания новых отраслей техники.

Физику чаще всего начинают изучать с раздела, называемого механикой. При этом механику принято делить на три крупных теории, которые применяются при определённых условиях - границах применимости. Это классическая механика, релятивистская механика, квантовая механика.
Механика
 |
| Классическая (начало положено Ньютоном сформулировавшем основные законы динамики) | Квантовая (В 1900 году Макс Планк выдвигает гипотезу об испускании света отдельными порциями – квантами.) | Релятивистская (В 1905 году создана специальная теория относительности) |
Глава II. Физические основы механики.
§ 5. Механическое движение.
8. Механика - часть физики, которая изучает закономерности механического движения и причины, вызывающие или изменяющие это движение.
Механическое движение – простейшая форма движения материи. Простота механического движения заключается в том, что мы наблюдаем его повседневно. Поэтому из всех естественных наук именно механика прежде других получила широкое развитие.
Механическим движением называют изменение положений тел или их частей друг относительно друга с течением времени.
Введём ряд понятий, которыми будем пользоваться при рассмотрении механического движения. Для анализа механического движения используются основные понятия кинематики: относительность движения, тело отсчёта, система отсчёта, материальная точка, траектория.
Обязательно нужно указать, по отношению к каким другим телам происходит движение.
Совокупность тел, выделенная для рассмотрения, называется механической системой.
Физика изучает не реальные объекты и явления, а их идеализации – модели, максимально приближенные к реальным объектам и явлениям.
Идеализации некоторых физических объектов.
Физика, в том числе и механика, для описания движения тел в зависимости от условий конкретных задач использует разные физические модели. Механические свойства тел определяются их химической природой, внутренним строением и состоянием, рассмотрение которых является предметом не механики, а других разделов физики. Поэтому для описания реальных движущихся тел используют ряд упрощённых моделей.
1. Материальная точка – тело, обладающее массой, размерами которого в данной задаче можно пренебречь (пример: Солнце и Землю можно считать материальными точками при рассмотрении движения Земли по орбите вокруг Солнца). Понятие материальной точки - абстрактное, но его введение облегчает решение физических задач. Движение материальной точки - простейшая задача механики, которая позволит рассмотреть более сложные типы движений. Произвольное макроскопическое тело или систему тел можно разбить на малые взаимодействующие части, сводящиеся к материальным точкам. Тогда изучение движения произвольной системы тел сводится к изучению системы материальных точек.
2. Абсолютно твёрдое тело – это тело, расстояние между точками которого есть величина постоянная, то есть тело не деформируется. Абсолютно твёрдое тело используют в задачах, в которых можно пренебречь деформацией.
3. Абсолютно упругое тело – это тело, деформация которого подчиняется закону Гука и которое после снятия нагрузки полностью восстанавливает свои первоначальные размеры и форму.
4. Абсолютно неупругое тело – это тело, деформация которого не подчиняется закону Гука, и состояние которого после снятия нагрузки не изменяется.
Выбор той или иной модели нужно производить так, чтобы учесть все существенные особенности поведения реального тела в данной задаче и отбросить все второстепенные, неоправданно усложняющие решение этой задачи.
Описать движение – значит представить его в виде набора физических величин, а для этого нужны средства измерения. Так как механическое движение происходит в пространстве и времени, то нам нужны средства измеряющие время и пройденное перемещение, что следует из определения механического движения.
Совокупность неподвижных друг относительно друга тел, по отношению к которым рассматривается движение, и отсчитывающих время часов, образует систему отсчёта.
Система отсчёта включает в себя:
 1. Тело отсчёта.
1. Тело отсчёта.
2. Жёстко связанная с телом отсчёта система координат.
3. Часы.
Примечание: движение одного и того же тела относительно различных систем отсчёта имеет, возможно, разный характер.
Теперь, введя основные понятия, можно сформулировать основную задачу кинематики: зная состояние системы в некоторый начальный момент времени, а также законы, описывающие движение, определить состояние системы, т. е. знать положение тела и его скорость, во все последующие моменты времени.
Любое механическое движение можно представить как комбинацию поступательного и вращательного движений.

 Механическое движение.
Механическое движение.
 Поступательное Поступательное
| Вращательное | ||
| Движение, при котором прямая, жёстко связанная с телом, остаётся параллельной самой себе. | .. | Движение, при котором все точки тела описывают окружности, центры которых лежат на одной прямой называемой осью вращения тела. |
В общем случае движение тела можно представить в виде сочетания этих двух видов движения:
Движение тела = поступательное движение + вращательное движение
Механическое движение можно изучать по разному. Можно его только описать, а можно исследовать его и выяснить причины, почему данное движение имеет именно такой вид. В соответствии с этим механику делят на три раздела:
 Механика
Механика
 |  | ||
| Кинематика (изучает движение тела без учёта причин вызывающих или изменяющих это движение) | Динамика (изучает движение тела с учётом причин вызывающих или изменяющих это движение) | Статика (изучает законы равновесия системы тел) |
Начнём изучение движения с кинематики, то есть изучим способы описания механического движения без учёта причин, которые вызывают его или изменяют.
 § 6. Перемещение. Скорость.
§ 6. Перемещение. Скорость.
9. Одной из задач механики является определение положения тела относительно других тел в любой момент времени, если известны начальные условия этого движения и уравнение движения. Эти уравнения содержат кинематические величины, которые характеризуют положение тела в пространстве, направление и быстроту движения тела, изменение движения тела.
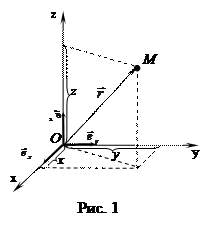
Пусть в некоторой точке пространства находится материальная точка (частица, тело) M. Опишем её положение относительно тела отсчёта – точки O. Это можно сделать с помощью вектора, который начинается в точке O и заканчивается в M. (рис.1).
Векторная величина, характеризующая положение тела в пространстве относительно других тел, направленная из начала координат к данному телу, называется радиусом - вектором.
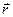 - обозначение радиуса - вектора. [6]
- обозначение радиуса - вектора. [6]
Радиус - вектор можно выразить через его проекции на координатные оси декартовой системы координат.
rx = x; ry = y; rz = z - компоненты радиуса - вектора, или: 
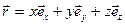 - разложение радиус-вектора по координатам.
- разложение радиус-вектора по координатам.
 - модуль радиуса - вектора.
- модуль радиуса - вектора.
Материальная точка при своём движении описывает линию, называемую траекторией.
Линия, вдоль которой движется тело, называется траекторией. [7]
По форме траектории движение можно разделить на прямолинейное, когда тело движется по прямой, и криволинейное, когда траектория движения представляет собой кривую.
Движение
(по форме траектории)

| Прямолинейное | Криволинейное |
Расстояние, отсчитанное вдоль траектории, называется пройденным путём.
Пройденный путь является скалярной величиной.
s - обозначение пройденного пути.
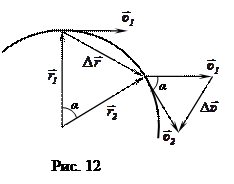
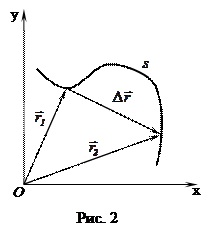 Пусть тело движется вдоль некоторой траектории, которая целиком расположена в одной плоскости (рис. 2). Такое движение называется плоским. Положение тела в момент времени t1 задаётся радиусом - вектором
Пусть тело движется вдоль некоторой траектории, которая целиком расположена в одной плоскости (рис. 2). Такое движение называется плоским. Положение тела в момент времени t1 задаётся радиусом - вектором  , а в момент времени t2 - радиусом вектором
, а в момент времени t2 - радиусом вектором  .
.
Приращение радиуса - вектора материальной точки при перемещении её из начального положения в конечное называется её перемещением.

 .
.
Учитывая, что положение тела изменяется с течением времени, можно записать:
 ,
,
или, так как вектор  изменяется со временем:
изменяется со временем:
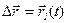 .
.
Таким образом движение тела можно описать с помощью зависимости радиуса - вектора этого тела от времени.

Скорость.
10. Различные тела за один и тот же промежуток времени совершают разные перемещения. Поэтому уместно ввести такую физическую величину, которая характеризовала бы быстроту
движения тела и его направление.
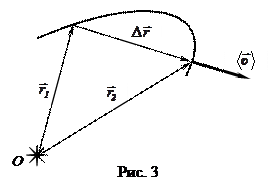 Скорость - векторная физическая величина, характеризующая быстроту и направление движения тела, численно равная отношению перемещения этого тела к промежутку времени, за который было совершено это перемещение.
Скорость - векторная физическая величина, характеризующая быстроту и направление движения тела, численно равная отношению перемещения этого тела к промежутку времени, за который было совершено это перемещение.
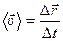 - средняя скорость.
- средняя скорость.
Направление вектора средней скорости совпадает с направлением вектора перемещения (рис. 3).
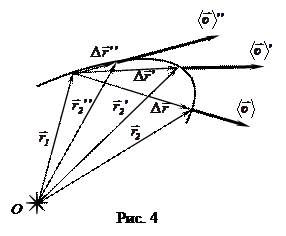 Будем уменьшать промежуток времени, за который происходит перемещение тела, при этом будет изменяться и положение вектора средней скорости. Если при достаточно длительном но конечном промежутке времени направление
Будем уменьшать промежуток времени, за который происходит перемещение тела, при этом будет изменяться и положение вектора средней скорости. Если при достаточно длительном но конечном промежутке времени направление  находилось как продолжение вектора перемещения (рис. 3), то при уменьшении промежутка времени Δ t положение вектора средней скорости стремится к предельному положению, а именно: при бесконечно малом промежутке времени Δ t вектор скорости направлен по касательной к траектории на данном бесконечно малом её участке, а сама скорость называется мгновенной.
находилось как продолжение вектора перемещения (рис. 3), то при уменьшении промежутка времени Δ t положение вектора средней скорости стремится к предельному положению, а именно: при бесконечно малом промежутке времени Δ t вектор скорости направлен по касательной к траектории на данном бесконечно малом её участке, а сама скорость называется мгновенной.
Мгновенной скоростью называется первая производная радиуса - вектора материальной точки по времени.
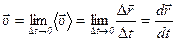 .
.
Вектор мгновенной скорости направлен по касательной к траектории в данной её точке.
Найдём модуль вектора мгновенной скорости.
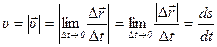 .
.
Модуль мгновенной скорости равен первой производной пройденного пути по времени.
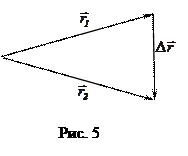 Примечание: нужно быть особо внимательными принаписании обозначений
Примечание: нужно быть особо внимательными принаписании обозначений 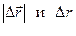 , ведь
, ведь 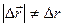 . Величина
. Величина 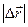 - это модуль приращения радиуса - вектора, а величина
- это модуль приращения радиуса - вектора, а величина 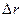 - это приращение модуля вектора
- это приращение модуля вектора 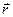 . Наиболее наглядно это можно показать на примере изменения направления одного и того же радиуса - вектора (рис. 5). В этом случае
. Наиболее наглядно это можно показать на примере изменения направления одного и того же радиуса - вектора (рис. 5). В этом случае  .
.
Теперь можно механическое движение разделить ещё на две группы.

| Равномерное (за одинаковые промежутки времени тело проходит равные расстояния) | Неравномерное (за одинаковые промежутки времени тело проходит неодинаковые расстояния) |
Единицы измерения скорости.
Единицы измерения скорости являются производными единицами, поэтому они выводятся из формулы для определения скорости.
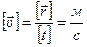 - в СИ.
- в СИ.
11. Часто для решения физических задач приходится представлять механическое движение в виде нескольких составляющих. Это выражается в разложении вектора скорости на составляющие. При этом раскладывать скорость на составляющие удобнее всего производить двумя способами.
Разложим вектор скорости по координатам:

Проекция вектора скорости на координатную ось равна производной по времени соответствующей координаты частицы.
С помощью проекций вектора скорости на оси координат можно вычислить и модуль скорости.
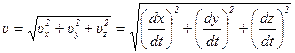 - модуль вектора скорости.
- модуль вектора скорости.
Рассмотрим ещё один способ разложения скорости на составляющие. Для этого представим вектор скорости в виде:
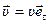 , где
, где 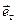 - орт вектора скорости, направленный по касательной
- орт вектора скорости, направленный по касательной
к траектории в рассматриваемой её точке, а радиус - вектор представим в виде 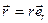 (рис. 6). Тогда:
(рис. 6). Тогда:
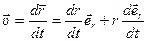 - что позволяет разложить вектор скорости
- что позволяет разложить вектор скорости
на две составляющие - радиальную и трансверсальную.
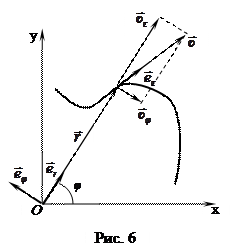 1. Радиальная составляющая направлена вдоль радиуса - вектора и характеризует быстроту изменения модуля радиуса - вектора:
1. Радиальная составляющая направлена вдоль радиуса - вектора и характеризует быстроту изменения модуля радиуса - вектора:
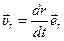 .
.
2. Трансверсальная составляющая направлена по нормали к радиусу - вектору и характеризует изменение радиуса - вектора по направлению:
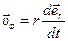 .
.
 Получим выражение для вычисления трансверсальной скорости. Пусть
Получим выражение для вычисления трансверсальной скорости. Пусть 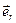 орт вектора
орт вектора 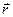 , который изменяется по направлению (рис. 7). При малом повороте его на угол Δ φ модуль приращения
, который изменяется по направлению (рис. 7). При малом повороте его на угол Δ φ модуль приращения 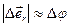 , тогда
, тогда  , где
, где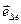 - единичный вектор для
- единичный вектор для  . При Δ φ → 0, т. е. при неограниченном уменьшении угла Δ φ, вектор
. При Δ φ → 0, т. е. при неограниченном уменьшении угла Δ φ, вектор 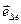 стремится к предельному положению при котором угол между
стремится к предельному положению при котором угол между  равен
равен  . Тогда
. Тогда 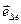 совпадает по направлению с вектором нормали к радиусу вектору:
совпадает по направлению с вектором нормали к радиусу вектору:
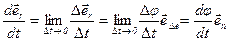 .
.
Тогда:
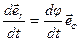 подставим в выражение для трансверсальной
подставим в выражение для трансверсальной
скорости:
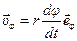 .
.
Модуль скорости с учётом такого разложения будет находиться так:
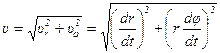 .
.
 Ещё один вопрос часто рассматривают в физике - нахождение средней величины за определённый промежуток времени, если задана функция изменения этой величины за рассматриваемый промежуток времени. В механике обычно находят среднюю скорость. Для определения средней путевой скорости тела нужно вычислить его пройденный путь. Как найти путь, проходимый телом с момента времени t1 до момента времени t2, зная величину скорости каждый момент времени? Для этого разобьём выбранный промежуток времени Δ t = t2 - t1 на N малых промежутков (рис. 8). Тогда за промежуток времени Δ ti тело пройдёт путь
Ещё один вопрос часто рассматривают в физике - нахождение средней величины за определённый промежуток времени, если задана функция изменения этой величины за рассматриваемый промежуток времени. В механике обычно находят среднюю скорость. Для определения средней путевой скорости тела нужно вычислить его пройденный путь. Как найти путь, проходимый телом с момента времени t1 до момента времени t2, зная величину скорости каждый момент времени? Для этого разобьём выбранный промежуток времени Δ t = t2 - t1 на N малых промежутков (рис. 8). Тогда за промежуток времени Δ ti тело пройдёт путь  , а весь путь:
, а весь путь:
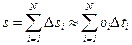 .
.
Полученное приближённое равенство тем точнее, чем меньше Δ ti, поэтому:
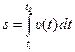 ,
,
а среднее значение путевой скорости с учётом выражения для нахождения пройденного пути можно найти так:
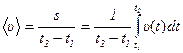 .
.
Можно записать полученные соотношения и в векторной форме:
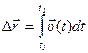 - перемещение тела за конечный промежуток времени,
- перемещение тела за конечный промежуток времени,
 - вектор средней скорости за конечный
- вектор средней скорости за конечный
промежуток времени.
Примечание: так как геометрический смысл определённого интеграла состоит в том, что определённый интеграл равен площади криволинейной трапеции, ограниченной графиком функции, то пройденный путь будет численно равен площади криволинейной трапеции, ограниченной графиком функции υ = υ (t) на рассматриваемом промежутке времени.
§ 7. Ускорение.
12. Ускорение - векторная физическая величина, характеризующая быстроту изменения вектора скорости по величине и направлению, и численно равная отношению приращения вектора скорости к промежутку времени, за который произошло это изменение.
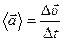 - среднее ускорение.
- среднее ускорение.
Здесь  - приращение вектора скорости.
- приращение вектора скорости.
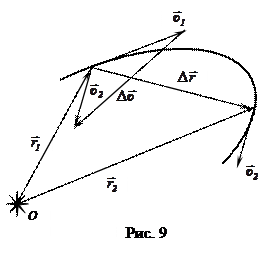 Направление вектора ускорения совпадает с направлением изменения вектора скорости
Направление вектора ускорения совпадает с направлением изменения вектора скорости 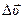 (рис. 9). Если бесконечно уменьшать промежуток времени Δ t, то в пределе получим мгновенное ускорение:
(рис. 9). Если бесконечно уменьшать промежуток времени Δ t, то в пределе получим мгновенное ускорение:
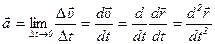 .
.
Мгновенное ускорение - это векторная величина равная первой производной вектора скорости по времени или второй производной радиуса - вектора по времени.
Примечание: ускорение играет по отношению к скорости такую же роль, какую скорость играет по отношению к радиусу - вектору.
Ускорение можно разложить на составляющие. Поэтому можно задать вектор ускорения с учётом проекций на координатные оси.
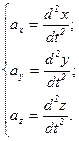
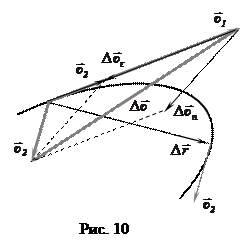 Есть и ещё один способ разложения вектора ускорения на составляющие. Вектор скорости может изменяться как по величине (
Есть и ещё один способ разложения вектора ускорения на составляющие. Вектор скорости может изменяться как по величине (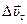 ), так и по направлению (
), так и по направлению ( ) (рис. 10). Поэтому ускорение можно представить в виде двух составляющих, одна из которых характеризует изменение вектора скорости по модулю, а другая по направлению. Это можно сделать с учётом, что:
) (рис. 10). Поэтому ускорение можно представить в виде двух составляющих, одна из которых характеризует изменение вектора скорости по модулю, а другая по направлению. Это можно сделать с учётом, что:
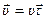 .
.
Тогда:
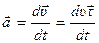 , откуда по правилам
, откуда по правилам
дифференцирования получим:
 .
.
Итак, получили два слагаемых для нахождения полного ускорения.
 |
Касательное
(тангенциальное)
 .
Направлена по касательной к траектории в точке.
Показывает изменение модуля скорости со временем.
Модуль тангенциального ускорения: .
Направлена по касательной к траектории в точке.
Показывает изменение модуля скорости со временем.
Модуль тангенциального ускорения:
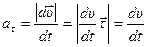 .
Если .
Если  - скорость растёт по величине и - скорость растёт по величине и
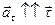 .
Если .
Если 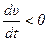 - скорость уменьшается и - скорость уменьшается и  .
Если .
Если 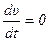 - движение равномерное. - движение равномерное.
| Нормальное
(центростремительное)
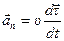 .
Направлена по нормали к траектории в точке.
Показывает изменение направления скорости со временем.
Модуль нормального ускорения тем больше, чем сильнее искривлена траектория.
Искривление траектории можно охарактеризовать двумя способами.
1. Кривизна: .
Направлена по нормали к траектории в точке.
Показывает изменение направления скорости со временем.
Модуль нормального ускорения тем больше, чем сильнее искривлена траектория.
Искривление траектории можно охарактеризовать двумя способами.
1. Кривизна: 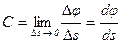 , где Δ φ - угол между касательными кривой в точках, отстоящих на Δ s (рис. 11).
2. Радиус кривизны: , где Δ φ - угол между касательными кривой в точках, отстоящих на Δ s (рис. 11).
2. Радиус кривизны: 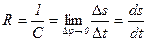 .
Если точки 1 и 2 расположены близко друг к другу, то: .
Если точки 1 и 2 расположены близко друг к другу, то:
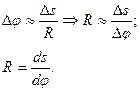 Так как
Так как 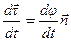 , а , а 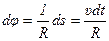 , то: , то:
 , подставив это
выражение в формулу для нормального ускорения получим: , подставив это
выражение в формулу для нормального ускорения получим:
 1- модуль нормального ускорения. 1- модуль нормального ускорения.
|
 Разложение вектора ускорения на составляющие производится следующим образом: сравнивают длины векторов скорости. Затем один из векторов скорости (например
Разложение вектора ускорения на составляющие производится следующим образом: сравнивают длины векторов скорости. Затем один из векторов скорости (например  ) достраивают на разность этих векторов (рис. 10). Затем сравнивают их направления.
) достраивают на разность этих векторов (рис. 10). Затем сравнивают их направления.
Итак, ускорение можно представить в виде двух составляющих:
 - полное ускорение тела.
- полное ускорение тела.
 - модуль полного ускорения.
- модуль полного ускорения.
§ 8. Классификация движения.
13. В зависимости от того, каковы по характеру тангенциальная и нормальная составляющие полного ускорения движения, конкретное движение можно отнести к тому или иному виду.
Виды движения:
1. aτ= 0, an= 0 - движение равномерное и прямолинейное;
2. aτ= const, an= 0 - движение равнопеременное и
прямолинейное;
3. aτ= f(t), an= 0 - движение с переменным ускорением по прямой;
4. aτ= 0, an= const - равномерное движение по окружности1;
5. aτ=0, an= f(t) - равномерное движение по кривой;
6. aτ= const, an= f(t) - равнопеременное движение по кривой;
7. aτ= f(t), an= f(t) - движение с переменным ускорением по кривой.
Уравнения равнопеременного прямолинейного движения.
14. Перечисленные выше виды движения описываются кинематическими уравнениями, которые получаются из определений скорости и ускорения. Рассмотрим, например, вывод уравнений равнопеременного прямолинейного движения, так как такой вид движения часто встречается на практике. Для этого запишем определения скорости и ускорения.
Ускорение:  ; так как движение прямолинейное и равнопеременное, то
; так как движение прямолинейное и равнопеременное, то  .
.
Скорость: 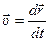 .
.
Получили два дифференциальных уравнения, которые нужно решить.

Решением данных дифференциальных уравнений являются функции, определяемые в результате интегрирования этих уравнений.
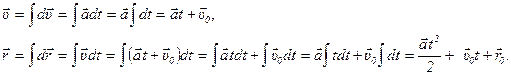
Таким образом, равнопеременное прямолинейное движение можно описать системой уравнений:
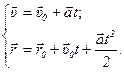
§ 9. Кинематика вращательного движения.
15. При вращательном движении тела каждая его точка будет перемещаться по окружности вокруг своей оси. Скорость и перемещение каждой точки будет зависеть от того, на каком расстоянии от оси эта точка находится. Поэтому понятиями скорости и перемещения (их называют линейными величинами), которыми описывали поступательное движение тела, пользоваться для описания вращения тела нельзя.
В кинематике вращательного движения тела используются угловые кинематические величины. Так, поворот тела при вращательном движении можно задать с помощью угла поворота.
Угол поворота можно задать в виде направленного отрезка, длина которого равна φ, а направление совпадает с осью вращения и связано с направлением вращения правилом правого винта (рис. 13).
Векторы, направление которых связано с направлением вращения, называются аксиальными векторами (псевдовекторами).
 Псевдовекторная величина, показывающая направление перемещения точек тела при вращении, численно равная углу поворота, называется угловым перемещением.
Псевдовекторная величина, показывающая направление перемещения точек тела при вращении, численно равная углу поворота, называется угловым перемещением.
Единица измерения углового перемещения в СИ:
 .
.
Примечание: повороты на конечные углы не складываются по правилу параллелограмма, и поэтому не являются векторами.[8]
Вращательное движение тела описывается кинематическим уравнением вращения.
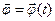 , где
, где 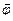 - вектор углового перемещения.
- вектор углового перемещения.
Вращение разных тел может носить разный характер. Одни тела, например, вращаются быстрее, а другие медленнее. Поэтому для характеристики вращения используют величины угловую скорость и угловое ускорение.
Псевдовекторная величина, характеризующая быстроту и направление вращения тела, равная отношению углового перемещения ко времени, за которое оно совершено, называется угловой скоростью тела.
 - средняя угловая скорость.
- средняя угловая скорость.
Направление угловой скорости совпадает с направлением оси вращения и связано с направлением вращения правилом правого винта (рис. 13).
Вращение с постоянной угловой скоростью называется равномерным. Равномерное вращение можно охарактеризовать периодом обращения и частотой.
Период обращения - время, за которое тело делает один оборот.
Для равномерного движения 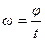 . Так как, один оборот составляет угол
. Так как, один оборот составляет угол  , а время одного полного оборота есть период Т, то:
, а время одного полного оборота есть период Т, то:
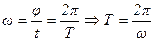 .
.
Частота вращения - число оборотов в единицу времени.
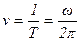 .
.
При неравномерном движении вращающегося тела угловая скорость его всё время изменяется. Тогда приходят к понятию мгновенной угловой скорости.
Мгновенной угловой скоростью вращающегося тела называют первую производную углового перемещения по времени.
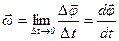 - мгновенная угловая скорость.
- мгновенная угловая скорость.
 - модуль мгновенной угловой скорости.
- модуль мгновенной угловой скорости.
Единица измерения угловой скорости в СИ:
 .
.
Изменение угловой скорости при вращении можно охарактеризовать угловым ускорением.
Псевдовекторная величина, характеризующая изменение вектора угловой скорости по величине и направлению, численно равная отношению изменения угловой скорости ко времени, за которое произошло это изменение, называется угловым ускорением.
 - среднее угловое ускорение.
- среднее угловое ускорение.
Если угловое ускорение меняется со временем, то вращение можно охарактеризовать с помощью мгновенного углового ускорения.
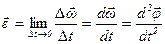 - мгновенное угловое ускорение.
- мгновенное угловое ускорение.
Вторая производная углового перемещения по времени или первая производная угловой скорости по времени есть мгновенное угловое ускорение.
Направление углового ускорения:
1. если движение вращающегося тела ускоренное, то  ;
;
2. если движение вращающегося тела замедленное, то 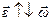 (рис. 13).
(рис. 13).
Единица измерения углового ускорения в СИ:

§ 10. Связь между угловыми и линейными величинами.
16. Отдельные точки вращающегося тела имеют различные линейные скорости  . В общем случае скорость каждой точки меняет своё направление непрерывно, а также может изменяться и модуль этой скорости, если вращение неравномерное. Найдём связи между угловыми и линейными величинами для произвольной точки вращающегося тела.
. В общем случае скорость каждой точки меняет своё направление непрерывно, а также может изменяться и модуль этой скорости, если вращение неравномерное. Найдём связи между угловыми и линейными величинами для произвольной точки вращающегося тела.
 Пусть за малый промежуток времени Δ t тело повернулось на угол Δ φ (рис. 14). Точка, отстоящая от оси вращения на расстоянии R, проходит при этом путь Δ s. Так как время поворота мало, то Δ s можно представить как
Пусть за малый промежуток времени Δ t тело повернулось на угол Δ φ (рис. 14). Точка, отстоящая от оси вращения на расстоянии R, проходит при этом путь Δ s. Так как время поворота мало, то Δ s можно представить как 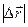 , откуда, используя теорему синусов, получим:
, откуда, используя теорему синусов, получим:
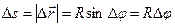 - так как при малом промежутке
- так как при малом промежутке
времени будет и малым угол поворота, то 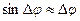 .
.
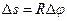 - связь между пройденным
- связь между пройденным
путём и углом поворота.
Можно получить связь между линейным перемещением и угловым. Так как и линейное перемещение, и угловое перемещение являются векторными величинами, то связь между ними можно будет записать как векторное произведение, порядок расстановки множителей в котором определяется по построению (рис. 14).
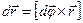 - связь между линейным и угловым перемещениями.
- связь между линейным и угловым перемещениями.
Найдём связь между линейной и угловой скоростями:
 .
.
Таким образом:
 - связь между модулем линейной скорости и
- связь между модулем линейной скорости и
модулем угловой скорости.
Если же положение рассматриваемой точки тела будет определяться радиусом - вектором, то можно найти выражение, связывающее векторы линейной и угловой скоростей. Для этого продифференцируем по времени выражение связи между линейным и угловым перемещениями.
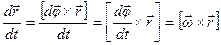 .
.
Таким образом:
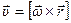 - связь между вектором линейной скорости
- связь между вектором линейной скорости
и вектором угловой скорости.
Полученное уравнение связи линейной и угловой скоростей хорошо согласуется с построением векторов угловой и линейной скоростей и радиуса - вектора (рис. 14).
Для нахождения связи между линейным ускорением и угловыми величинами будем по отдельности рассматривать равномерное и неравномерное вращения.
Сначала рассмотрим равномерное движение точки по окружности. Вектор линейной скорости точки при таком движении будет изменяться только по направлению. Тогда, каждая точка вращающегося равномерно тела будет иметь нормальное (центростремительное) ускорение. Отсюда, используя связь между линейной и угловой скоростями, получаем:
 - модуль нормального ускорения.
- модуль нормального ускорения.
Если ввести перпендикулярный к оси вращения вектор 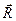 , проведённый от этой оси в данную точку тела, то для этой точки:
, проведённый от этой оси в данную точку тела, то для этой точки:
 - связь между нормальным ускорением и угловыми
- связь между нормальным ускорением и угловыми
величинами.
Знак «минус» стоит из-за противоположного направления векторов 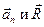 .
.
Если же вращение неравномерное, то нужно для каждой точки определить и тангенциальное (касательное) ускорение:
 .
.
Таким образом:
 - связь между тангенциальным (касательным) и
- связь между тангенциальным (касательным) и
угловым ускорениями.
Учитывая, что тангенциальное ускорение точки, угловое ускорение являются векторными величинами, а положение точки задаётся радиусом-вектором, можно записать:
 .
.
Поместим угловые и линейные кинематические величины в таблицу, из которой видно, что вращательное и поступательное движения описываются аналогичными величинами.
| Величина | Линейная | Угловая | Связь между величинами |
| Перемещение |
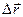 ; ; 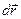
|
 ; ; 
|
 ; ; 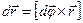
|
| Скорость |
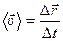 ; ; 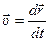
|
 ; ; 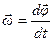
|
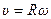 ; ; 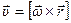
|
| Ускорение | 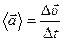 ; ; 
|  ; ;

|
 ; ;  ; ;  ; ; 
|
Уравнения равнопеременного вращения.
17. Уравнения равнопеременного вращения получаются из определений угловой скорости и углового ускорения. Эти уравнения получаются аналогично тому, как выводятся уравнения равнопеременного прямолинейного движения. Запишем определения угловой скорости и углового ускорения.
Угловое ускорение: 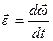 ; так как вращение равнопеременное, то
; так как вращение равнопеременное, то 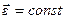 .
.
Скорость: 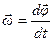 .
.
Получили два дифференциальных уравнения, которые нужно решить.
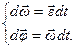
Решением данных дифференциальных уравнений являются функции, определяемые в результате интегрирования этих уравнений.
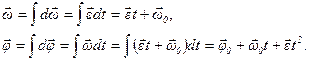
Таким образом, равнопеременное вращение можно описать системой уравнений:

§ 11. Динамика материальной точки.
Взаимодействие.
18. Рассмотрим типы движения и условия их осуществления:
| Равномерное, прямолинейное осуществляется, если на тело не действуют другие тела, тело движется по инерции. | Неравномерное, прямолинейное; неравномерное, непрямолинейное; равномерное, непрямолинейное осуществляются, если на тело действуют другие тела, тело движется в результате взаимодействия. |
Таким образом, тип движения определяется некоторой причиной, а именно: если на тело не оказывается никакого воздействия, то тело движется по инерции, а воздействие на тело других тел приводит к движению не по инерции. К этому выводу человечество пришло уже давно, поэтому и возникла необходимость изучать взаимодействие тел. Несмотря на огромное количество различных взаимодействий различных тел, все взаимодействия можно свести к четырём фундаментальным их видам.
Виды фундаментальных взаимодействий:
1. Гравитационное – обусловлено всемирным тяготением, осуществляется между телами обладающими массами.
2. Слабое – отвечает за многие процессы распада элементарных частиц.
3. Электромагнитное – осуществляется через электрические и магнитные поля между электрически заряженными телами.
4. Сильное (ядерное) – обеспечивает связь частиц в атомном ядре.
Виды фундаментальных взаимодействий расположены в порядке возрастания их интенсивностей.
Движение тел с учётом причин вызывающих или изменяющих его изучается динамикой.
В основе классической или ньютоновской механики[9] лежат три закона динамики, сформулированные Ньютоном в 1687 году.
Законы Ньютона являются результатом обобщения большого количества опытных фактов.
Как и любая теория, классическая механика имеет границы применимости.
Границы применимости классической механики:
1. Тела должны иметь размеры и массы не меньше размеров и масс атомов.
2. Тела должны двигаться с малыми скоростями по сравнению со скоростью света в вакууме.
Примечание: уравнения релятивистской механики в пределе (для скоростей, малых по сравнению со скоростью света в вакууме) переходят в уравнения классической механики, то есть классическая механика – частный случай релятивистской механики. А уравнения квантовой механики дают в пределе (для размеров и масс тел, больших по сравнению с размерами и массами атомов) уравнения классической механики, то есть классическая механика является предельным случаем квантовой механики.
В рамках классической механики имеют дело с гравитационным и электромагнитным взаимодействием, которые являются фундаментальными – их нельзя свести к другим, более простым взаимодействиям.
Пространство и время в классической механике.
Перед рассмотрением законов Ньютона обратим внимание на один момент. Механическое движение происходит в пространстве и во времени. Как соотносятся эти две категории в классической механике? Для того чтобы дать ответ на этот вопрос, нужно опять обратиться к многовековому опыту человечества. На основе этих накопленных знаний, Ньютон сформулировал, казалось бы, очевидное представление о пространстве и времени.
В классической механике пространство и время рассматриваются независимо друг от друга [10], то есть существует независимое пространство – безотносительное к чему-либо внешнему вместилище вещей, остающееся всегда одинаковым и неподвижным, и абсолютное время – когда два события, одновременные в какой-либо системе отсчёта, будут одновременными и во всех остальных.
§ 12. Первый закон Ньютона.
19. Рассмотрим I закон Ньютона. Для его формулирования рассмотрим движение тела по наклонной плоскости.
Движение по инерции.
 Галилео Галилей экспериментально установил так называемый закон инерции. Он показал, что при отсутствии сопротивления тело под действием постоянной силы будет двигаться равноускоренно, и установил, что ускорение тяжёлого тела, движущегося по гладкой наклонной плоскости, обратно пропорционально длине этой плоскости при постоянной её высоте (рис. 15). Отсюда были получены интересные выводы.
Галилео Галилей экспериментально установил так называемый закон инерции. Он показал, что при отсутствии сопротивления тело под действием постоянной силы будет двигаться равноускоренно, и установил, что ускорение тяжёлого тела, движущегося по гладкой наклонной плоскости, обратно пропорционально длине этой плоскости при постоянной её высоте (рис. 15). Отсюда были получены интересные выводы.
1. При l = h получаем:  , так как
, так как 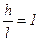 . Имеем случай свободного падения тела с ускорением
. Имеем случай свободного падения тела с ускорением 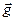 .
.
2. При 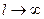 получаем:
получаем:  . Имеем случай движения по инерции.
. Имеем случай движения по инерции.
Таким образом, в пределе движение тела по гладкой горизонтальной плоскости без сопротивления будет происходить без всякого ускорения:
 .
.
I закон Ньютона.
Полученное выше утверждение о движении тел по гладкой горизонтальной плоскости без сопротивления можно обобщить на больший круг движений: если на тело не действуют другие тела, то оно будет двигаться прямолинейно и равномерно или покоиться. В таком виде наше утверждение принято называть законом инерции, который впервые был сформулирован Галилеем. Этот закон и был затем обобщён и сформулирован Ньютоном как первый закон динамики материальной точки, который подтверждён многочисленными опытами. Рассмотрим его несколько формулировок:
1-я формулировка: материальная точка, бесконечно удалённая от остальных тел, будет сохранять своё состояние покоя или равномерного и прямолинейного движения.
Примечание: покой – частный случай равномерного и прямолинейного движения.
С учётом примечания, попробуем сформулировать I закон Ньютона так, чтобы он задавал условие, при котором движение по инерции перестаёт быть таковым.
2-я формулировка: всякое тело находится в состоянии равномерного и прямолинейного движения, пока воздействие со стороны других тел не заставит его изменить это состояние.
Первый закон Ньютона выполняется не во всякой системе отсчёта. Если рассматривать движение тела с постоянной скоростью из двух систем отсчёта, движущихся с ускорением друг относительно друга, то в одной системе движение тела будет движением по инерции, а в другой – ускоренным. В таких системах отсчёта I закон Ньютона не выполняется одновременно. Следовательно, существует два типа систем отсчёта.
Система отсчёта, в которой выполняется I закон Ньютона, называется инерциальной.
Си
Дата добавления: 2014-01-14; Просмотров: 1137; Нарушение авторских прав?; Мы поможем в написании вашей работы!