Уравнения движения массивных звеньев

Движение звеньев описывается уравнениями движения. Существует большой ряд способов формирования уравнений движения. В лекциях мы рассмотрим 2 наиболее часто используемых способа: уравнения Лагранжа 2-го рода и уравнения, построенные с использованием принципа Д’Аламбера. Вы их уже изучали в теоретической механике. В лекциях мы рассмотрим принципы их формирования в больших динамических системах.

Уравнения движения Лагранжа 2-го рода представляются в виде.

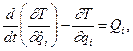
где Т - кинетическая энергия движущихся звеньев; 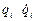- обобщенные перемещения и скорости движения звеньев; - обобщенная сила, действующая на звенья в направлении обобщенных перемещений.

При относительно простой записи уравнений движения, тщательно учитывающих все особенности взаимодействия тел, сложность представляет выражение кинетической энергии системы и обобщенных сил через обобщенные координаты и скорости.

Рассмотрим формирование уравнений движения на примере плоской задачи динамики буксируемого орудия (см. рис 8).

В качестве массивных звеньев можно принять:

¾ лафет (нижний и верхний станки, соединенные боевым штырем и механизмом горизонтального наведения в единую конструкцию), перемещающийся в плоскости чертежа по трем направлениям - двум поступательным и одному угловому.

¾ качающаяся часть (люлька с перемещающимися откатными частями), перемещающаяся относительно лафета в угловом направлении.

¾ откатные части (ствол с казенником и установленными на нем механизмами), перемещающиеся по направляющим вдоль оси стрельбы (отката).

¾ снаряд, перемещающийся вдоль оси канала ствола.

Для удобства записи индексов введем следующие сокращенные обозначения массивных звеньев: лафет - лф, качающаяся часть - кч, откатные части - от,
снаряд - сн.

В качестве упругих звеньев принимают опорные устройства, которыми лафет опирается на грунт (станины, сошники, колеса, поддон у тяжелых орудий);

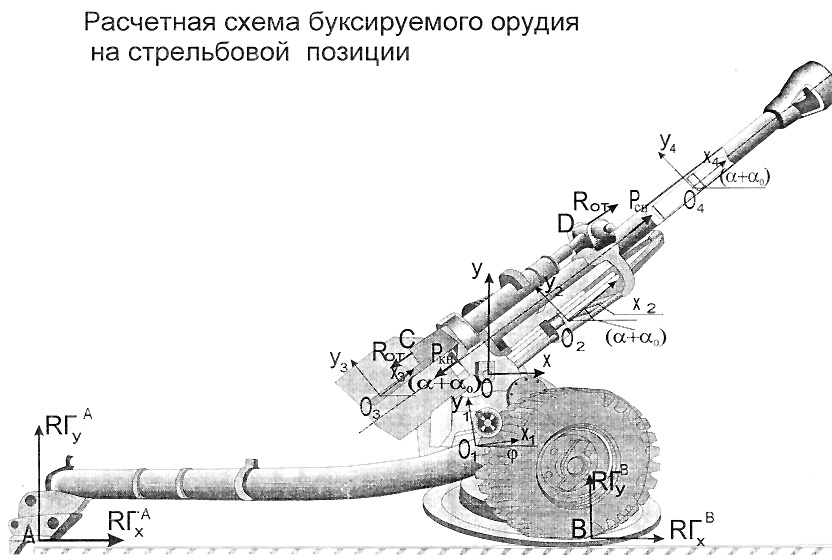Рис.8 Расчетная схема артиллерийской установки

подъемный механизм, соединяющий качающую часть с лафетом;

противооткатные устройства (тормоз отката и накатник), соединяющие люльку и откатные части;

пороховой газ, внутри канала ствола, воздействующий на откатные части снаряд при выстреле.

Последние два упругих звена являются типично нелинейными и нередко задаются законом изменения параметров, определяемым из решения задачи внутренней баллистики и отката.

Для упрощения вывода малоинерционные звенья, связанные с движением узлов механизмов орудия не рассматриваем.

Таким образом, физическая модель включает 4 элемента (ЭФМ):

- стойка (грунт) - лафет;

- лафет - качающаяся часть;

- качающаяся часть - откатные части;

- откатные части - снаряд.

Дата добавления: 2014-01-14