Давление под изогнутой поверхностью жидкости

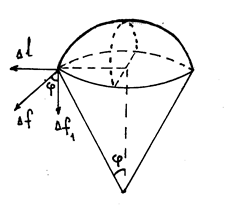
Поверхностная пленка жидкости по своим свойствам сходна с растянутой упругой пленкой. Поэтому если пленка ограничена плоским контуром, то она и сама стремится принять форму плоскости. Отсюда, выпуклая пленка, стремясь стать плоской, давит на слои, а выгнутая их растягивает. Другими словами: всякая изогнутая поверхностная пленка оказывает на жидкость добавочное давление по сравнению с тем, которое испытывает жидкость с плоской поверхностной пленкой. В случае выпуклой по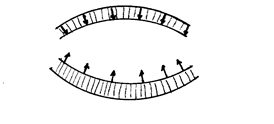верхности это добавочное давление положительно, в случае вогнутой – отрицательно. Определим значение этого добавочного давления для случая, когда поверхность жидкости представляет собой часть сферы радиуса R. Выделим малый сферический сегмент 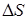. Силы поверхностного натяжения, приложенных к контуру этого сегмента, повсюду касательная к сферической поверхности. Рассмотрим силу 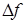, приложенную к элементу контура 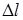. Эта сила равна

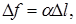(1)

где α – коэффициент поверхностного натяжения.

Силу 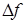можно разложить на составляющие по направлению параллельные радиусу ОС и перпендикулярные радиусу ОС. Рассмотрим составляющую 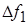параллельную ОС. Поскольку мы рассматриваем выпуклую поверхность, то центр С лежит внутри жидкости. Поэтому сила 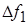сжимает жидкость, лежащую под сегментом 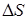(положительное давление). Если же поверхность вогнута, то центр С лежит вне жидкости и в этом случае сила 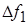растягивает жидкость (отрицательное давление).

Из рис. видно, что

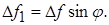
откуда используя (1), имеем

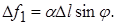
Эта сила приложена к элементу контура 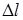. Ко всему сферическому сегменту 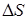приложена сила параллельная ОС.

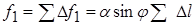
Здесь 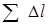- длина контура, равная длине окружности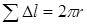

Т. о.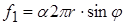

Из рис. видно 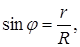отсюда .

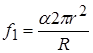Давление Р получим, поделив значение этой силы на площадь круга радиуса r. Откуда 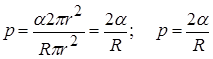(3)

Эта формула дает нам значение добавочного давления р, оказывающего на жидкость со стороны сферической поверхности. Из формулы (3) видно, что давление прямо пропорционально коэффициенту поверхностного натяжения и обратно пропорционально радиусу поверхности R. Чем сильнее искривлена поверхность, тем меньше R и следовательно больше Р.

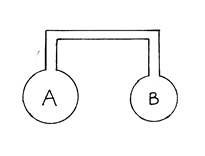Наличие добавочного давления объясняет ряд физических явлений. Например, внутри мыльного пузыря воздух находится под большим давлением, чем внешний воздух. Размерность давлений воздуха, внутри и вне пузыря тем больше, чем меньше R. Этим объясняется опыт иллюстрированный на рис. На концах стеклянной трубки выдуть два мыльных пузыря А и В разных диаметров.

Дата добавления: 2014-01-14