Давление под изогнутой поверхностью жидкости любой формы

Выражение, полученное выше для добавочного давления р для случая сферической поверхности может быть обобщено и на изогнутую поверхность любой формы. Для этого введем понятие о кривизне произвольной формы.

К произвольной поверхности в т. О восстановим перпендикуляр ON. Проводим через нормаль ON плоскости р ₁ и р ₂. Линия пересечения этой плоскости с поверхностью называется нормальным сечением. Мы рассмотрим два нормальных сечения по дуге А ₁ ОВ ₁ и А ₂ ОВ ₂ с радиусом кривизны ОС ₁= R ₁ и ОС ₂= R ₂ В геометрии доказывается, что если через т. О любой кривой поверхности провести два взаимно перпендикулярных нормальных сечения А ₁ В ₁ и А ₂ В ₂, радиусы кривизны которых равны R ₁ и R ₂, то величина

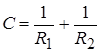
имеет одно и то же значение для любой пары таких взаимно перпендикулярных сечений. Эта величина С называется средней кривизной поверхности в т. О. выберем теперь на кривой поверхности, имеющей произвольный вид, т. О и проведем через эту т. два взаимно перпендикулярных нормальных сечения А ₁ В ₁ и А ₂ В ₂ с радиусами кривизны R ₁ и R ₂. Выделим около т. О малый линейный четырехугольник ДЕF6. Длина дуги 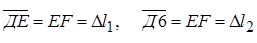. Тогда площадь четырехугольника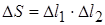

Найдем силу поверхностного натяжения 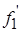, приложенную к краям ДЕ

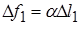
Давление, действующее на ис-сть со стороны изогнутой поверхности

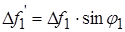
Приближенно можно считать

Дуга а отрезок ОС ₁ представляет собой R ₁ нормального сечения А ₁ В ₁. Откуда 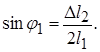Подставляя значени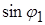я для имеем

На край действует сила

Рассуждая аналогично, находим, что на край 6Д действует сила параллельная ОС

.

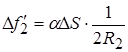Такая же составляющая действует на край ЕF. Т. о., параллельно ОС ₁ действует сила

Величина в скобках – среднее значение кривизны в т. О и не зависит от выбора нормальных сечений А ₁ В ₁ и А ₂ В ₂. Давление р ₁ оказываемое изогнутой поверхностью на ис-сть.

формула Лапласа

В случае сферы R ₁ = R ₂ =R и что совпадает с ранее полученной формулой.

Дата добавления: 2014-01-14