Особенности определения усилий в двухветвеиных колоннах

При двухветвенных колоннах расчет поперечной рамы с учетом пространственной работы каркаса здания аналогичен расчету рамы со сплошными колоннами. Двухветвевая колонна представляет собой многоэтажную однопролетную раму (рамный стержень) с расстоянием с между ветвями осей, расстоянием s между осями распорок, числом панелей n, длиной b нижней рамной части, длиной а верхней сплошной части, общей длиной l (рис. ХШ.25, а). Поскольку ригелями рамного стержня служат короткие жесткие распорки, а стойками — менее |жесткие ветви колонны, деформациями ригелей можно пренебречь и с практически достаточной точностью считать их абсолютно жесткими. Другая возможная расчетная схема - с упругими ригелями, — как показали ис­следования, приводит к несущественному уточнению результатов расчета. Для определения реакций при неподвижной верхней опоре двухветвенную колонну рассматривают как стержень, обладающий изгибной жестко­стью Е_bI₁ и конечной сдвиговой жесткостью К.

Сдвиго­вая жесткость двухветвенной колонны обусловлена местным изгибом ветвей, она равна силе, вызывающей единичный угол перекоса ветвей (рис. XIII.25, б):

где I - момент инерции ветви.

Рис. XI 11.25. Расчетные схемы двухветвенных колонн

Приложим к верхнему концу рассматриваемого стер­жня пока без верхней опоры силу Х=1 (рис. XIII.25, в). Тогда перемещение

здесь I_i = I₁ - в нижней части колонны; I_i=I₂ — в верх­ней части.

Отсюда реакция от перемещения ∆=1 верхнего кон­ца колонны (рис. XIII.25, г)

h — момент инерции верхней части колонны; А — площадь сечения ветви; 1=Ас²/2 - момент инерции нижней части колонны (значени­ем 2I здесь пренебрегают как относительно малым); α=a/1.

Допустим, двухветвенная колонна загружена крано­вым моментом М.

Найдем перемещение

Теперь найдем реакцию R при неподвижной верхней эпюре двухветвенной колонны (рис. XIП.25, д)

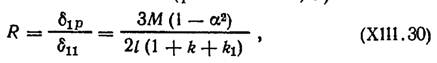
здесь знак минус опущен.

Аналогично найдем значения реакций R двухветвенной колонны для других нагрузок, которые приведе­ны в приложении XII.

Формулы реакций R универсальны, так как могут применяться не только для двухветвенных колонн, но также для сплошных ступенчатых колонн при k=0,

колонн сплошных постоянного сечения при k₁=k=0. По этим же формулам в необходимых случаях можно найти перемещения δ₁₁ =l/R_∆; δ_1р = R/RA, а также выполнить расчет рамы с учетом упругой заделки колонны в фунда­менте.

При расчете рамы на изменение температуры ∆t учет действительной податливой заделки колонны в фундамен­те (а также учет действительной жесткости колонны на участках с трещинами) приводит к уменьшению изгиба­ющего момента. Реакция от поворота колонны в нижнем сечении на угол φ=1 составит

Найдем реактивный момент от поворота фундамента |на угол φ=1 (рис. XIII.26). Осадка края фундамента с размерами сторон в плане hxb составит y=0,5htgφ=0,5h (деформациями самого фундамента пренебрегаем). Краевое давление фундамента на основание

где С - коэффициент постели при неравномерном обжатии основания (см. гл. XII).

Реактивный момент от поворота фундамента

|

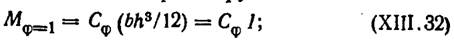здесь СφI - угловая жесткость фундамента.

Пример XIII.1. Определить реакцию R_∆ двухветвенной колонны

Рис. XI 11.26. К расчету подат­ливости заделки колонны

Рис. XI 11.27. К определению усилий в ветвях и распорах колонны

Пример XIII.2. Определить реакцию двухветвенной колонны от ветровой нагрузки интенсивностью υ по данным примера ХШ.1.

Решение. Вычисляем реакцию

Пример XIII.3. Определить реакцию R сплошной ступенчатой колонны от кранового момента М=500 кН-м по данным: l=11,1 м; a=3,85 м; b=7,25 м; I₂=1; I₁=8.

Решение. Определив расчетные значения а=0,35; k = 0,3, при k₁=0, найдем реакцию,

Пример XII 1.4. Определить реакцию R сплошной колонны по­стоянного сечения длиной l=11,1 м от кранового момента M =500 кН-м, приложенного на расстоянии с=3,85 м.

Решение. Определив, а=0,35, при k=k₁=0 найдем реакцию

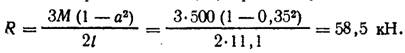
После определения из расчета поперечной рамы упру­гих реакций Re усилия в расчетных сечениях М, N, Q вычисляют относительно геометрической оси двухветвенной колонны, усилия же в ветвях и распорках определя­ют в последующем расчете при подборе сечений. Продольные силы в ветвях колонны

где М, N - расчетные усилия по оси двухветвенной колонны;

При определении коэффициента η следует учесть влияние гибкости ветвей в плоскости изгиба двухветвен­ной колонны как для составного сечения (рис. ХШ.27,а). Приведенный радиус инерции г²_red зависит от радиуса инерции сечения нижней части колонны г²₁ = =с²/4 и от радиуса инерции сечения ветви r²=h²/12.

Приведенная гибкость должна удовлетворять условию

После подстановки значений г₁² и г² и сокращения на l²₀ получим

отсюда

здесь n=h1/s — число панелей двухветвенной колонны.

Условная критическая сила в соответствии с форму­лой гл. IV

здесь A, μ - площадь сечения и коэффициент армирования ветви. При определении коэффициента

моменты М и M_l вычисляют относительно оси, проходя­щей через ось ветви.

Изгибающий момент ветвей при нулевой точке мо­ментов в середине высоты панели (рис. XIII.27, б)

Изгибающий момент распорки равен сумме моментов ветвей в узле

Поперечная сила распорки

Если одна из ветвей при определении продольной си­лы по формуле (XIII.33) окажется растянутой, то следу­ет выполнить расчет двухветвенной колонны с учетом пониженной жесткости этой растянутой ветви. В этом случае изгибающие моменты в сжатой ветви и распор­ках определяют из условия передачи всей поперечной си­лы в сечении колонны на сжатую ветвь.

Дата добавления: 2014-01-14