Метод простых итераций

В ряде случаев весьма удобным приемом уточнения корня уравнения является метод последовательных приближений (метод итераций).

Пусть с точностью 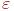необходимо найти корень уравнения f(x)=0, принадлежащий интервалу изоляции [a,b]. Функция f(x) и ее первая производная непрерывны на этом отрезке.

Для применения этого метода исходное уравнение f(x)=0 должно быть приведено к виду 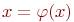(4.2)

В качестве начального приближения 0 выбираем любую точку интервала [a,b].

Далее итерационный процесс поиска корня строится по схеме: (4.3)

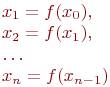
В результате итерационный процесс поиска реализуется рекуррентной формулой (4.3). Процесс поиска прекращается, как только выполняется условие

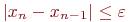(4.4)

или число итераций превысит заданное число N.

Для того, чтобы последовательность х1, х2,…, хn приближалась к искомому корню, необходимо, чтобы выполнялось условие сходимости:

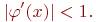(4.5)

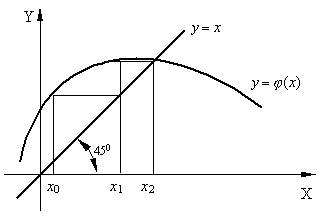
Рис. 4.6. Геометрический смысл метода

Переходим к построению схемы алгоритма (рис. 4.7). Вычисление функции 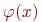оформим в виде подпрограммы.

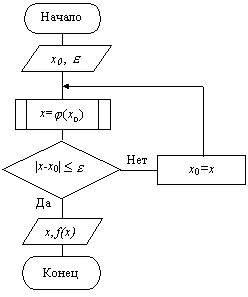
Рис. 4.7. Схема алгоритма уточнения корня методом итераций

Метод Ньютона (метод касательных)

Рассмотренные ранее методы решения нелинейных уравнений являются методами прямого поиска. В них для нахождения корня используется нахождение значения функции в различных точках интервала [a,b].

Метод Ньютона относится к градиентным методам, в которых для нахождения корня используется значение производной.

Дано нелинейное уравнение:

f(x)=0

Найти корень на интервале [a,b] с точностью .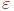

Метод Ньютона основан на замене исходной функции f(x), на каждом шаге поиска касательной, проведенной к этой функции. Пересечение касательной с осью Х дает приближение корня (Рис. 4.8).

Выберем начальную точку x0=b (конец интервала изоляции). Находим значение функции в этой точке и проводим к ней касательную, пересечение которой с осью Х дает нам первое приближение корня x1.

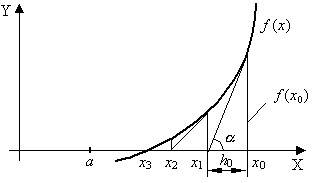
Рис. 4.8.

x1 = x0 – h0,

где

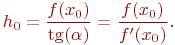
Поэтому

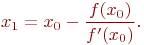
В результате итерационный процесс схождения к корню реализуется рекуррентной формулой

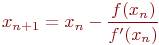(4.6)

Процесс поиска продолжаем до тех пор, пока не выполнится условие:

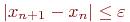(4.7)

Упростим условие (4.7), исходя из (4.6). Получим:

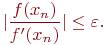(4.8)

Метод обеспечивает быструю сходимость, если выполняется условие:

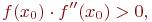(4.9)

т.е. первую касательную рекомендуется проводить в той точке интервала [a,b], где знаки функции f(x0) и ее кривизны f"(x0) совпадают.

Схема алгоритма уточнения корня метод Ньютона приведена на рис. 4.9

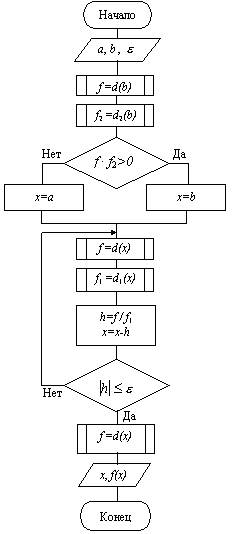
Рис. 4.9. Схема алгоритма уточнения корня методом Ньютона

Модифицированный метод Ньютона (метод секущих)

В этом методе для вычисления производных на каждом шаге поиска используется численное дифференцирование по формуле:

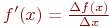
Тогда рекуррентная формула (4.6) будет иметь вид:

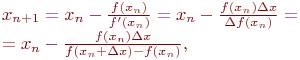(4.10)

где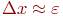

Дата добавления: 2014-01-14