Следствия из аксиом вероятности

1. .

Доказательство. Свойство непосредственно следует из равенства 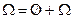и аксиомы 3.

2. Для любого события А .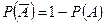

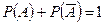Доказательство. Так как , то по аксиомам 2 и 3 . Следовательно, и .

3. Для любого случайного события А .

Доказательство. Свойство непосредственно следует из 1 и 2 и свойства 1.

4. Если событие А влечёт за собой событие В, то .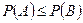

Доказательство. Событие В может быть представлено в виде 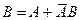. Отсюда в силу аксиом 3 и 1 получаем .

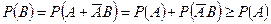5. Для произвольных событий А и В .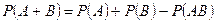

Доказательство. Поскольку в суммах 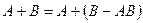и 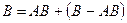слагаемые являются несовместными событиями, то в соответствии с аксиомой 3

и 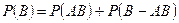, тогда

, откуда следует

.

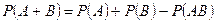Замечание. Свойство 5 называют теоремой сложения для произвольных событий А и В.

Пример 1. Вероятности попадания в цель при стрельбе первого и второго орудий соответственно равны: ; 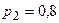. Оба орудия выстрелили по цели. Найти вероятность попадания хотя бы одним из орудий.

Решение. Пусть событие А – попадание в цель первого орудия, событие В – попадание в цель второго орудия. Вероятность попадания в цель каждым из орудий не зависит от результата стрельбы из другого орудия, поэтому события А и В независимы. Вероятность события АВ (оба орудия попали в цель) 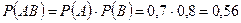. Так как события А и В совместны, то искомая вероятность .

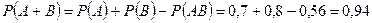Следствие 1. Для произвольных событий А и В .

Доказательство следует из .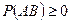

Следствие 2. Если 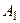, , 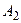…, 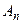- произвольные события, то .

Доказательство проводится по индукции.

Замечание. Система аксиом Колмогорова непротиворечива так как существуют реальные объекты, которые всем этим аксиомам удовлетворяют.

Пример. Пусть , , , , 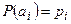, 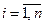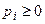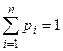. Положив 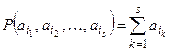, удовлетворим аксиомам Колмогорова.

Система аксиом Колмогорова неполна: даже для одного и того множества 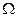вероятности в множестве 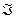можно выбрать разными способами.

Пример. Игральная кость. 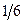или и . Симметричная и несимметричная кости.

Неполнота системы аксиом теории вероятностей не является свидетельством их неудачного выбора или недостаточной работы по их созданию, а вызвана существом дела: в различных задачах могут встретиться явления, при изучении которых требуется рассматривать одинаковые множества случайных событий, но с различными вероятностями.

Дальнейшее развитие теории нуждается в дополнительном предположении, которое называется расширенной аксиомой сложения. Необходимость новой аксиомы объясняется тем, что в теории вероятностей постоянно приходится рассматривать события, подразделяющиеся на бесконечное число частных случаев.

Аксиома 4 (расширенная аксиома сложения). Если событие А равносильно наступлению хотя бы одного из попарно несовместимых событий 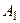, , 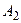…, , …, 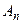то .

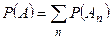Замечание. Расширенная аксиома сложения может быть заменена равносильной ей аксиомой непрерывности.

Аксиома 4’ (аксиома непрерывности). Если последовательность событий 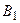, , 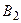…, , … такова, что каждое последующее влечёт за собой предыдущее и произведение всех событий есть невозможное событие, то .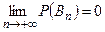

Теорема 1. Расширенная аксиома сложения и аксиома непрерывности эквивалентны.

Доказательство. 1. 4 – 4’. Пусть события 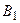, , 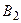…, , … таковы, что 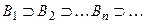и для любого выполняется равенство (*).

Очевидно, что

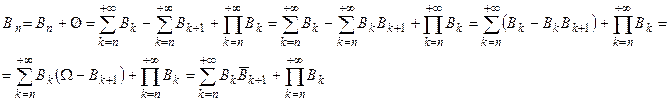
Так как события, стоящие в этой сумме попарно несовместны, то согласно расширенной аксиоме сложения . Но в силу условия (*) 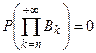. Поэтому . То есть 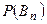есть остаток сходящегося ряда . Поэтому .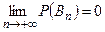

2. 4’ – 4. Пусть события 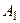, , 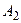…, , …, 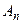попарно несовместны и . Положим 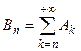. По построению для любого . Если событие наступило, то наступило какое-нибудь из событий (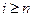) и, значит, в силу попарной несовместности событий 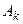, события 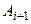, , 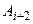… уже не наступили. Таким образом, события , , 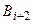… невозможны, следовательно, невозможно событие 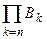. По аксиоме непрерывности 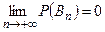. Так как 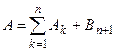, то по обычной аксиоме сложения .

Замечание. Аксиоматика Колмогорова позволяет строить теорию вероятностей как часть теории меры, а вероятность рассматривать как неотрицательную нормированную аддитивную функцию множества.

Определение 4. Вероятностным пространством принято называть тройку символов 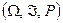, где 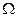– множество элементарных событий, 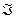– 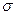-алгебра подмножеств 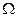, называемых случайными событиями, – вероятность, определённая на 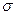-алгебре .

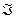Дата добавления: 2014-01-14