Формулы Байеса

Теорема. Пусть выполняются условия теоремы о полной вероятности и имеет место (5). Тогда условная вероятность события 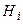в предположении, что событие 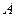уже произошло, определяется по формулам:

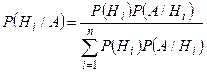(). (6)

Вероятности 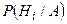, вычисленные по формулам Байеса, называют вероятностями гипотез.

Доказательство. Согласно теореме умножения вероятностей имеем ():

.

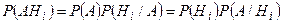Отсюда 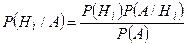или ().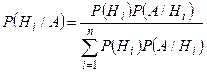

Замечание. Общая схема применения формул (6) такова. Пусть событие А может протекать в различных условиях, относительно характера которых может быть сделано n гипотез 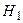, , 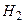…, . По тем или иным причинам известны вероятности 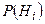этих гипотез до испытания. Известно также, что гипотеза 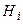сообщает событию А вероятность 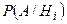. Произведён опыт, в котором событие А наступило. Это должно вызвать переоценку вероятностей гипотез 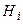. Формулы Байеса позволяют количественно решить этот вопрос. (Пристрелка).

Пример 8. Детали, изготовляемые цехом завода, попадают для проверки их на стандартность к одному из двух контролеров. Вероятность того, что деталь попадет к первому контролеру, равна 0,6, а ко второму – 0,4. Вероятность того, что деталь будет признана стандартной первым контролером, равна 0,94, а вторым – 0,98. Деталь при проверке была признана стандартной. Найти вероятность того, что её проверил первый контролер.

Решение. Обозначим через 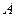событие, состоящее в том, что деталь признана стандартной, гипотеза 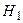– деталь проверил первый контролер, гипотеза 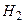– деталь проверил второй контролер. По условию задачи имеем:

(вероятность того, что деталь попадет к первому контролеру),

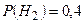(вероятность того, что деталь попадет ко второму контролеру),

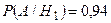(вероятность того, что деталь будет признана стандартной первым контролером),

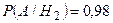(вероятность того, что деталь будет признана стандартной вторым контролером).

Искомую вероятность того, что признанную стандартной деталь проверил первый контролер, найдём по формуле Байеса:

.

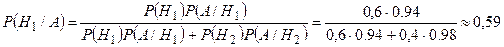До испытания вероятность гипотезы 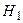равнялась 0,6, а после того, как стал известен результат испытания, условная вероятность этой гипотезы изменилась и стала равной 0,59.

Пример 9. Решить для примера 7.

Глава 2. Последовательность независимых испытаний

Дата добавления: 2014-01-14