Проецирование на три плоскости проекций

Прежде чем перейти к проецированию на три плоскости проекций, остановимся на построении проекций с числовыми отметками. В проекциях с числовыми отметками плоскость проекций П _i называют плоскостью нулевого уровня и обозначают П ₀. Идея этого метода состоит в том, что на плоскость П ₀ ортогонально проецируют точку и вместе с проекцией точки задают ее расстояние до плоскости П ₀ (рис. 1.4). Это расстояние называют числовой отметкой точки и задают обычно в метрах. Числовую отметку точки пишут внизу справа от обозначения ее изображения.

Рис. 1.4.

Если плоскость нулевого уровня расположена горизонтально, то чертеж называют планом. На плане всегда указывают линейный масштаб и при необходимости дают ориентацию относительно сторон света.

Очень удобно в проекциях с числовыми отметками изображать линии уровня, все точки которых имеют одинаковые отметки. Линии уровня проецируются на П ₀ без искажения своей формы (применяется в картографии).

Проекции с числовыми отметками позволяют просто решать многие задачи. Обратимость чертежей в проекциях с числовыми отметками очевидна.

Зарождение идеи этого метода относят к средним векам. Уже тогда многие народы, пользующие картами с показаниями морских глубин, умели изображать точку при помощи ее проекции и отметки. Однако теоретическое обоснование метод получил лишь в 19 веке (французский военный инженер – капитан Нуазе, 1823г.).

Чертежи в проекциях с числовыми отметками построены на одной плоскости проекций – на одной картине и часто называются однокартинными.

Информацию о расстоянии точки относительно плоскости проекции можно дать не с помощью числовой отметки, а с помощью связанных между собой двух или трех проекций точки, построенной на плоскостях проекций. Полученный таким образом чертеж называют комплексным. Основные принципы построения таких чертежей изложены Г. Монжем.

Гаспар Монж крупный французский геометр конца 18, начала 19 веков, 1789-1794 гг. один из основателей знаменитой политехнической школы в Париже и участник работ по введению метрической системы мер и весов.

Постепенно накопившиеся отдельные правила, и приемы таких изображений были приведены в систему и развиты в труде Г. Монжа "Geometric descriptive".

Изложенный Монжем метод ортогонального проецирования на две (три) взаимно перпендикулярные плоскости проекций обеспечивает выразительность, точность и удобоизмеримость изображений предметов на плоскости, был и остается основным методом составления технических чертежей.

В соответствии с методом, предложенным Г. Монжем, рассмотрим в пространстве три взаимно перпендикулярные плоскости проекций (рис.1.5).

Рис. 1.5

Условимся называть:

• плоскость p₁ – горизонтальной плоскостью проекций;

• плоскость p₂ – фронтальной плоскостью проекций;

• плоскость p₃ – профильной плоскостью проекций.

Линии пересечения плоскостей проекции образуют оси координат. Ось х называют осью абсцисс, ось у – осью ординат и ось z – осью апликат. Точка пересечения координатных осей принимается за начало координат и обозначается буквой О. Положительным направлением осей координат считают: для оси х – влево от начала координат; оси у – в сторону наблюдателя от плоскости p₂; ось z – вверх от плоскости p₁.

Задание точки на комплексном чертеже Монжа

Геометрический объект любой сложности можно рассматривать как геометрическое место точек, по взаимному расположению, которых можно составить представление об объекте, а по расположению их относительно системы координат можно судить о положении его в пространстве. Точка одно из основных понятий геометрии. При систематическом изложении геометрии точка обычно принимается за одно из исходных понятий.

Пусть дана точка А в пространстве (рис. 1.5). Положение точки А определяется тремя координатами (х, у, z), показывающими величины расстояний, на которые точка удалена от плоскостей проекций.

Точки А¢, А ¢¢, А ¢¢¢, в которых пересекаются перпендикулярные прямые, проведенные из этой точки, называются ортогональными проекциями точки А: А ¢ – горизонтальная проекция, А ¢¢ – фронтальная проекция; А ¢¢¢ – профильная проекция точки А.

Прямые (АА ¢), (АА ¢ ¢), (АА ¢¢ ¢) называются проецирующими прямыми или проецирующими лучами. При этом прямую (АА ¢) называют горизонтально проецирующей прямой, (АА ¢¢) – фронтально проецирующей, (АА ¢¢ ¢) – профильно проецирующей прямой.

Две проецирующие прямые, проходящие через точку А, образуют плоскость, которую называют проецирующей.

Для получения плоского чертежа, состоящего из указанных проекций, плоскости p₁ и p₃ совмещают с фронтальной плоскостью проекций p₂. Для этого плоскость p₁ поворачивают на 90° вокруг оси х по часовой стрелке, а плоскость p₃ поворачивают вокруг оси z против часовой стрелки (рис.1.6).

Полученный таким образом проекционный чертеж, называется эпюром (франц. Epure – чертеж.). Эпюр часто называют эпюром Монжа или комплексным чертежом Монжа.

Плоскости проекций делят пространство на четыре двугранных угла – четверти. Рассматривая ортогональные проекции, предполагают, что наблюдатель находится в первой четверти на бесконечно большом расстоянии от плоскостей проекций.

Геометрические объекты делятся на: линейные (точка, прямая, плоскость), нелинейные (кривая линия, поверхность) и составные (многогранники, одномерные и двумерные обводы).

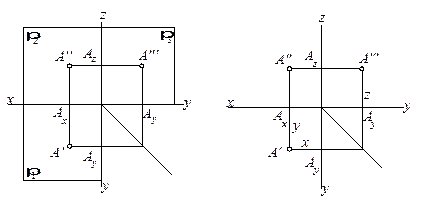
Рис. 1.6

Точка на комплексном чертеже Монжа может занимать общее положение, т.е. находиться вне плоскости проекций (рис. 1.6), и частное положение – находиться на одной из плоскостей проекций, сразу на двух плоскостях проекций или одновременно на трех.

На рис. 1.7 изображена точка, принадлежащая фронтальной плоскости проекций, координата y которой равна нулю.

На рис. 1.8 показана точка, лежащая на горизонтальной плоскости проекций, а
на рис. 1.9 на профильной.

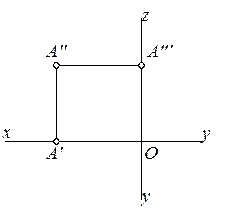
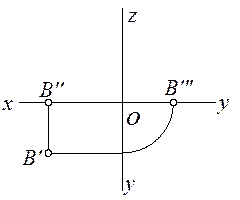
Рис. 1.7	Рис. 1.8

Точка, находящаяся одновременно на двух плоскостях проекций, изображена на рис. 1.10. Она принадлежит плоскостям p ₁ и p ₂, т.е. лежит на оси x. Две проекции А¢ и А¢¢ совпадают, а третья А¢¢¢ находится в точке начала координат. Точка, находящаяся на трех плоскостях проекций, есть начало координат О.

Рис. 1.9	Рис. 1.10

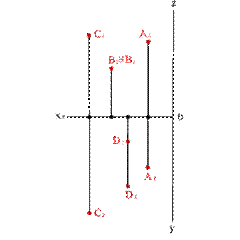
Рис. 1.11

На рисунке 1.11 представлены точки A B C D, расположенные в разных четвертях пространства и их эпюр (A – в первой четверти, B – во второй, C – в третьей и D – в четвертой четверти).

Контрольные вопросы по теме лекции:

1. Сущность центрального и параллельного проецирования.

2. Как располагаются и называются плоскости проекций?

3. В чем сущность метода Монжа? Что такое комплексный чертеж (эпюр) Монжа?

4. Что называется проекцией точки?

5. Какими координатами определяется каждая из проекций точки?

6. Где находится проекция точки, принадлежащей одной из плоскостей проекций, двум плоскостям проекций, трем плоскостям проекций?

7. Как по чертежу определить расстояние точки до плоскостей p₁, p₂, p₃.

Рекомендуемая литература по изучению дисциплины «Начертательная геометрия»:

1. Гордон В.О., Семенцов–Огиевский М.А. Курс начертательной геометрии. М.: 2000.

2. Гордон В.О., Иванов Ю.Б., Солнцева Т.Е. Сборник задач по курсу начертательной геометрии. М.: Высш.шк., 2004.

3. Локтев О.В. Краткий курс начертательной геометрии. М.: 2001.

4. Локтев О.В. Задачник по начертательной геометрии. М.: Высш.шк., 1999.

5. Муртазина Д.Н. Конспект лекций. Казань, КГЭУ, 2003.

Дата добавления: 2014-01-14