Лекция № 2. Тема лекции: Задание прямой на комплексном чертеже Монжа

Тема лекции: Задание прямой на комплексном чертеже Монжа. Взаимное положение прямых. Теорема о проекции прямого угла. (раздел 1)

1. Изображение прямых общего и частных положений.

2. Взаимное положение прямых: параллельные, пересекающиеся, скрещивающиеся прямые.

3. Плоские углы. Теорема о проекции прямого угла.

4. Определение натуральной величины отрезка прямой методом прямоугольного треугольника.

Задание прямой на комплексном чертеже Монжа

При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии. Если основой построения геометрии служит понятие расстояния между двумя точками пространства, то прямую линию можно определить как линию, вдоль которой расстояние между двумя точками является кратчайшим.

Рассматривая прямую линию как кратчайшее расстояние между некоторыми точками A и B, проекция прямой определяется как геометрическое место проекций отдельных положений точки, образующей прямую.

Совокупность проецирующих линий отдельных точек прямой образует плоскость, называемую проецирующей плоскостью. Она перпендикулярна плоскости проекций. Таким образом, проекцию прямой AB (рис. 2.1) можно рассматривать как линию пересечения проецирующей плоскости с плоскостью проекций.

Рис. 2.1	Рис. 2.2

Следовательно, проекция прямой на плоскость есть прямая. Поэтому для ее построения достаточно спроецировать две любые точки данной прямой а, например, точки A и B, и через построенные проекции A ¢ и B ¢ провести прямую, которая и будет проекцией данной прямой на плоскость p (рис. 2.2).

Прежде чем перейти к проецированию прямой на три плоскости, отметим некоторые свойства (инварианты) параллельного проецирования:

· проекция точки есть точка;

· проекция прямой есть прямая;

· если точка принадлежит прямой, то проекция этой точки принадлежит проекции прямой;

· отрезок прямой линии, параллельной плоскости проекций, проецируется на эту плоскость в истинную величину, т.е., если AA ¢ = BB ¢, то A¢B ¢ = AB (рис. 2.3);

· прямая, перпендикулярная плоскости проекций проецируется на эту плоскость в виде точки (рис. 2.4);

· длина проекции отрезка прямой, наклоненного к плоскости проекций, меньше истинной его длины и зависит от величины угла наклона прямой к плоскости проекций (A¢B ¢ = AB cos φ °) (рис. 2.5).

· если отрезок прямой делится точкой в каком-либо отношении, то проекция отрезка делится проекцией этой точки в том же отношении (рис. 2.5).

Рис. 2.3	Рис. 2.4
Рис. 2.5

Из сравнения трапеций ABB¢A ¢ и ACC¢A ¢ можно получить соотношение AB: BC = A¢B¢:B¢C ¢. Следствие: середина отрезка изображается серединой его проекции.

Изображение прямых общего и частных положений

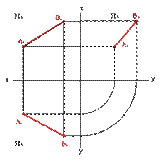
Пусть прямая АВ (рис. 2.6) непараллельна ни одной из плоскостей проекций. Спроецировав ее на три плоскости, получим ее проекции: А ¢ В ¢ – горизонтальную, А ² В ² – фронтальную, А ¢¢¢ В ¢¢¢ – профильную.

Рис. 2.6

Совместив плоскости проекций, получим эпюр прямой АВ (рис. 2.6).

Если прямая задана только двумя проекциями, третью проекцию строят по двум любым точкам прямой (рис. 2.7).

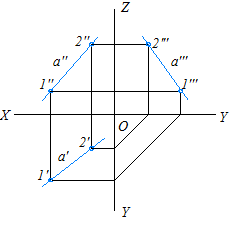
Рис. 2.7

В зависимости от положения прямой по отношению к плоскостям проекций она может занимать как общее, так и частные положения:

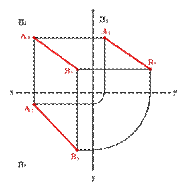
1. Прямая непараллельная ни одной плоскости проекций называется прямой общего положения (рис. 2.8).

Рис. 2.8

2. Прямые параллельные плоскостям проекций, занимают частное положение в пространстве и называются линиями уровня:

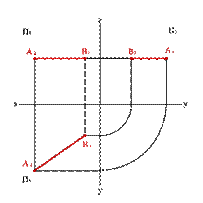
· прямые параллельные горизонтальной плоскости проекций называются горизонтальными линиями уровня или горизонталями (рис. 2.9). Высота или уровень всех ее точек одинакова, поэтому ее фронтальная проекция h ² параллельна оси x, что является ее графическим признаком на эпюре. Горизонтальная проекция отрезка выражает ее истинную величину, а также показывает истинные величины углов наклона прямой к плоскостям проекций: p₂ – угол b и p ₃ – угол g;

· прямые параллельные фронтальной плоскости проекций называются фронтальными линиями уровня или фронталями (рис. 2.10). Все ее точки одинаково удалены от плоскости p₂, поэтому ее горизонтальная проекция f ¢ параллельна оси x. Угол a – угол наклона прямой к плоскости p₁, угол g – к плоскости p₃;

	Рис. 2.9
Рис. 2.10

· прямые параллельные профильной плоскости проекций называются профильными (рис. 2.11). Все ее точки одинаково удалены от плоскости p₃, поэтому ее горизонтальная и фронтальная проекции параллельны оси z. Различают восходящую и нисходящую профильные прямые. Первая по мере удаления от зрителя поднимается, вторая - понижается.

Рис. 2.11

3. Прямые, перпендикулярные плоскостям проекций, называются проецирующими. Прямая перпендикулярная одной плоскости проекций, параллельна двум другим. В зависимости от того, какой плоскости проекций перпендикулярна исследуемая прямая, различают:

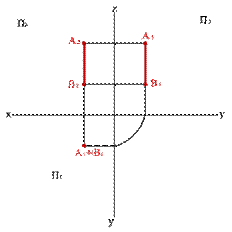
· горизонтально проецирующую прямую (рис. 2.12);

Рис. 2.12

· фронтально проецирующую прямую (рис. 2.13);

Рис. 2.13

· профильно проецирующую прямую (рис. 2.14);

Рис. 2.14

Дата добавления: 2014-01-14