Взаимное пересечение плоскостей

Позиционные задачи

Лекция № 4

Тема лекции: Позиционные задачи. Взаимное пересечение плоскостей. Пересечение прямой с плоскостью. (раздел 2)

1. Позиционные задачи.

2. Построение линии пересечения плоскостей.

3. Определение точки пересечения прямой с плоскостью.

Решение многих задач способами начертательной геометрии, в конечном счете, сводится к определению позиционных и метрических характеристик геометрических объектов. Позиционныезадачи – задачи, решение, которых должно давать ответ на вопрос о взаимном расположении геометрических объектов как по отношению друг к другу, так и относительно системы координатных плоскостей проекций.

Для построения проекции линии пересечения двух плоскостей необходимо предварительно рассмотреть следующие частные задачи.

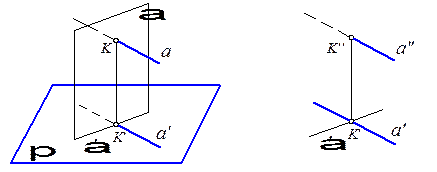
Задача 1. Построить проекции точки пересечения К прямой а с проецирующей плоскостью a (рис. 4.1 и 4.2).

Основываясь на свойстве горизонтально проецирующей плоскости, согласно которому горизонтальные проекции всех точек, принадлежащих этой плоскости, располагаются на ее проекции a ¢, устанавливаем, что горизон­тальная проекция точки, принадлежащей и прямой а и плоскости a, есть точка К ¢, в которой горизонтальная проекция прямой а пересекается с проекцией плоскости a. По горизонтальной проекции К ¢ искомой точки, проведя линию связи, получаем на а ² фронтальную проекцию К ² точки пересечения прямой а с плоскостью a.

Рис. 4.1	Рис. 4.2

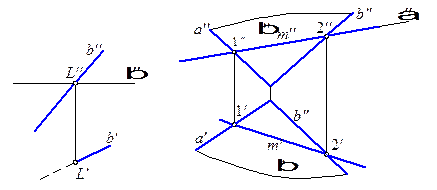
На рис. 4.3 показано построение проекций точки L прямой b с горизонтальной плоскостью уровня b.

В этом случае очевидной является фронтальная проекция L ¢¢ искомой точки. Линия связи определяет на горизонтальной проекции прямой b горизонтальную проекцию точки L.

Задача 2. Построить проекции линий пересечения проецирующей плоскости a с плоскостью общего положения b (рис. 4.4).

Фронтальная проекция m ¢¢ линии пересечения данных плоскостей совпадает с проекцией a ¢¢ фронтально проецирующей плоскости a.

Искомая линия m определяется точками 1 и 2, в которых плоскость a пересекает прямые а и b, которыми задана плоскость b. По фронтальным проекциям 1¢¢ и 2¢¢ этих точек находят их горизонтальные проекции 1¢ и 2¢, а проведя через них прямую получаем горизонтальную проекцию m ¢ линии пересечения данных плоскостей.

Рис. 4.3	Рис. 4.4

Линия пересечения двух плоскостей есть прямая, а потому построение этой линии сводится или к нахождению двух точек, общих обеим плоскостям, или к нахождению одной общей точки и определению направления искомой линии.

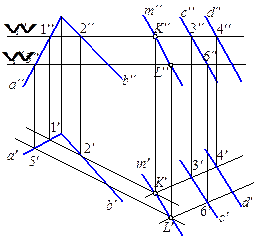
Пусть даны две плоскости общего положения a и b, для которых требуется построить проекции их линии пересечения (рис. 4.5 и рис. 4.6).

Поскольку данные плоскости являются плоскостями общего положения, установить направление их линии пересечения не представляется возможным и, следовательно, искомую прямую приходится определять двумя точками.

Для нахождения точки, принадлежащей обеим плоскостям, применяется следующий прием:

• пересекаем обе данные плоскости какой-либо проецирующей плоскостью w1 (обычно применяется плоскость уровня);

• строим две линии 1-2 и 3-4, по которым проведенная вспомогательная плоскость пересекает данные плоскости;

• находим точку К, в которой построенные прямые пересекаются между собой.

Очевидно, эта точка будет принадлежать обеим данным плоскостям, а следовательно, и линии их пересечения.

Для нахождения второй общей точки L следует пересечь данные плоскости второй вспомогательной плоскостью w2 и проделать вышеуказанные построения.

Прямая, проведенная через точки К и L, является искомой линией пересечения плоскостей a и b.

Рис. 4.5

Рис. 4.6

Дата добавления: 2014-01-14